
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Путь, перемещение и радиус кривизны.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Путь, перемещение и радиус кривизны.
Путь – скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Перемещение (s{век}) - вектор, соединяющий начальную и конечную точки траектории; измеряется в метрах (м). Радиус кривизны - величина, обратная кривизне кривой. Радиус кривизны характеризует величину соответствия кривой от прямой.
Связь радиус-вектора, скорости и ускорения. Смысл скорости и ускорения.
v=dr/dt a=dv/dt Скорость характеризует быстроту изменения положения тела относительно данной системы отсчета и является векторной физической величиной. Ускорение – векторная физическая величина, характеризующая быстроту изменения скорости.
Нормальное и тангенциальное ускорение.
Тангенциальное ускорение – ускорение, характеризующее быстроту изменения модуля скорости при криволинейном движении.
Нормальное ускорение – ускорение, характеризующее быстроту изменения направления вектора скорости при криволинейном движении.
Связь угла поворота, угловой скорости и углового ускорения.
Угловая скорость — векторная физическая величина, характеризующая скорость вращения материальной точки вокруг центра вращения. Вектор угловой скорости по величине равен углу поворота точки вокруг центра вращения в единицу времени:
а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Угловое ускорение — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости материальной точки. При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости
и направлен по касательной к годографу вектора
Связь угловых и линейных величин.
Законы Ньютона.
1) Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения. 2) В инерциальной системе отсчёта ускорение, которое получает материальная точка с постоянной массой, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе.
3) Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
7. Силы в механике (вид, к чему приложена, куда направлена, чему равна). Сюда относятся силы упругости, сила трения, сила тяжести, вес. Сила – физическая величина, являющаяся количественной мерой воздействия одного тела на другое, в результате которого тело приобретает ускорение или деформируется. Сила упругости — сила, возникающая при деформации тела и противодействующая этой деформации. Действует в любом сечении деформированного тела, а также в месте его контакта с телом, вызывающим деформации. Вектор силы противоположен направлению деформации тела (смещению его молекул). Природа упругих сил электромагнитная. Закон Гука: Силой трения - сила, которая возникает при движении одного тела по поверхности другого. Сила трения всегда направлена вдоль поверхности соприкосновения в сторону, противоположную движению. Сила трения прямо пропорциональна весу тела (P) и силе нормальной реакции (N) и зависит от того, насколько сильно тела прижаты друг к другу. Сила тяжести – сила, действующая на тело со стороны Земли и сообщающая телу ускорение свободного падения (Fт=mg). Направление силы тяжести - вертикаль в данной точке земной поверхности. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести Fт=GMm/R2 . СИЛА ТЯЖЕСТИ, сила P, действующая на любое тело, находящееся вблизи земной поверхности, и определяемая как геометрическая сумма силы притяжения Земли F и центробежной силы инерции Q, учитывающей эффект суточного вращения Земли. Вес тела – сила, в которой вследствие притяжения к Земле тело действует на свою опору или подвес. В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес - это упругая сила, приложенная к опоре или подвесу (т. е. к связи). Вес тела направлен в одну сторону с силой тяжести и равен P=m(g±a).
Закон всемирного тяготения. Все тела взаимодействуют друг с другом с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.
Момент силы. Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы. M= F·l= F·r·sin(α), где r — расстояние от центра вращения до места приложения силы (метр), α — угол, между вектором силы F и вектором положения r. Направление вектора момента силы определяется правилом буравчика, а величина его равна M. →M=→F ·→r
Момент импульса. Момент импульса материальной точки относительно точки O определяется векторным произведением Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц, из которых состоит тело относительно оси. Учитывая, что Производная момента импульса твердого тела по времени равна сумме моментов всех сил, действующих на тело: Закон сохранения импульса. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Закон сохранения энергии. Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
Работа и мощность. Работой A, совершаемой постоянной силой Мощность — это работа за единицу времени (1 с):
Уравнение Бернулли. Уравнение Бернулли — для стабильно текущего потока (газа или жидкости) сумма кинетической и потенциальной энергии, давления на единицу объема является постоянной в любой точке этого потока.
Первое и второе слагаемое в Законе Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. А третье слагаемое в нашей формула является работой сил давления и не запасает какую-либо энергию. Из этого можно сделать вывод, что размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости или газа.Постоянная в правой части уравнения Бернулли называется полным давлением и зависит в общих случаях, только от линии потока.
Характеристики колебаний. Для описания колебательного движения существуют следующие характеристики: амплитуда, частота, период колебаний, циклическая частота. Модуль максимально в озможного смещения относительно положения равновесия называется амплитудой колебания А. Промежуток времени, в течение которого происходит одно полное колебание, называется периодом колебания Т. Измеряется в секундах. Число колебаний за одну секунду называется частотой
Циклическая частота
Гармонические колебания. Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или
где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд; Обобщенное гармоническое колебание в дифференциальном виде
Силы инерции. Силы инерции — силы, обусловленные ускоренным движением неинерциальной системы отсчета (НСО) относительно инерциальной системы отсчета (ИСО). Они направлены в сторону, противоположную уско рению. Силы инерции возникают только в системе отсчета, движущейся с ускорением, т. е. это кажущиеся силы.
Основные положения МКТ. Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ. В основе молекулярно-кинетической теории лежат три основных положения:
Адиабата Пуассона Для идеальных газов, чью теплоёмкость можно считать постоянной, в случае квазистатического процесса адиабата имеет простейший вид и определяется уравнением:
Теорема Карно. Первая теорема Карно. КПД обратимого цикла Карно, осуществляемого между двумя источниками теплоты, не зависит от свойств рабочего вещества, с помощью которого этот цикл осуществляется.
Вторая теорема Карно. КПД необратимого цикла Карно всегда меньше обратимого цикла Карно, осуществляемого между одними и теми же источниками теплоты, имеющими постоянные, но разные температуры.
Третья теорема Карно. Обратимый цикл Карно имеет наибольший КПД по сравнению с любыми обратимыми или необратимыми циклами, в которых наибольшая и наименьшая температуры равны соответственно температуре горячего источника и температуре холодного источника цикла Карно.
Уравнение Ван-дер-Ваальса. Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса. Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой. Для одного моля газа Ван-дер-Ваальса оно имеет вид:
где · · · · Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка Для
где · Путь, перемещение и радиус кривизны.
Путь – скалярная физическая величина, определяемая длиной траектории, описанной телом за некоторый промежуток времени. Перемещение (s{век}) - вектор, соединяющий начальную и конечную точки траектории; измеряется в метрах (м). Радиус кривизны - величина, обратная кривизне кривой. Радиус кривизны характеризует величину соответствия кривой от прямой.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1133; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.145.168 (0.009 с.) |



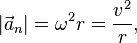 где ω — угловая скорость относительно центра вращения, а r — радиус окружности.
где ω — угловая скорость относительно центра вращения, а r — радиус окружности. ,
, по времени, то есть
по времени, то есть ,
, в соответствующей его точке.
в соответствующей его точке.






 , где
, где  — радиус-вектор, проведенный из точки O,
— радиус-вектор, проведенный из точки O, 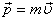 — импульс материальной точки.
— импульс материальной точки.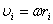 , получим
, получим  .
.

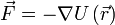 ,
, ,
,

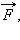 называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус углаα между векторами силы
называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус углаα между векторами силы  и перемещения
и перемещения 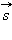 : A = F*s* cosα
: A = F*s* cosα


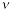 . Измеряется в герцах (Гц). Если частота равна 1 Гц, то это значит, что за одну секунду тело совершает одно колебание.
. Измеряется в герцах (Гц). Если частота равна 1 Гц, то это значит, что за одну секунду тело совершает одно колебание.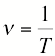
 - это величина на
- это величина на  больше частоты. Она показывает сколько колебаний совершается за
больше частоты. Она показывает сколько колебаний совершается за 

 ,
,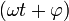 — полная фаза колебаний,
— полная фаза колебаний,  — начальная фаза колебаний.
— начальная фаза колебаний.
 — сила инерции, действующая на тело относительно поступательно движущейся НСО.
— сила инерции, действующая на тело относительно поступательно движущейся НСО. 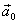 — ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе;
— ускорение НСО относительно ИСО. Она появляется, например, в самолете при разгоне на взлетной полосе; — центробежная сила инерции, действующая на тело относительно вращающейся НСО.
— центробежная сила инерции, действующая на тело относительно вращающейся НСО.  — угловая скорость НСО относительно ИСО,
— угловая скорость НСО относительно ИСО,  — расстояние от тела до центра вращения;
— расстояние от тела до центра вращения; — кориолисова сила инерции, действующая на тело, движущееся со скоростью
— кориолисова сила инерции, действующая на тело, движущееся со скоростью  относительно вращающейся НСО.
относительно вращающейся НСО.  — угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта).
— угловая скорость НСО относительно ИСО (вектор направлен вдоль оси вращения в соответствии с правилом правого винта). где
где  — его объём,
— его объём,  — показатель адиабаты,
— показатель адиабаты,  и
и  — теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
— теплоёмкости газа соответственно при постоянном давлении и постоянном объёме.
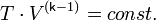


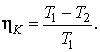

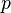 — давление,
— давление, — молярный объём,
— молярный объём, — абсолютная температура,
— абсолютная температура,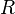 — универсальная газовая постоянная.
— универсальная газовая постоянная. учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка
учитывает силы притяжения между молекулами (давление на стенку уменьшается, так как есть силы, втягивающие молекулы приграничного слоя внутрь), поправка  — объем молекул газа.
— объем молекул газа. молей газа Ван-дер-Ваальса уравнение состояния выглядит так:
молей газа Ван-дер-Ваальса уравнение состояния выглядит так:
 — объём,
— объём,


