
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Момент инерции и его физический смысл. Теорема Штейнера.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Момент инерции представляет собой меру инерции тела во вращательном движении. Теорема Штейнера. Момент инерции
Закон сохранения импульса. В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.
Закон сохранения момента импульса. Если сумма моментов сил, действующих на тело, вращающееся вокруг неподвижной оси, равна нулю, то момент импульса сохраняется (закон сохранения момента импульса): Закон сохранения энергии. Полная механическая энергия замкнутой системы тел, между которыми действуют только консервативные силы, остаётся постоянной.
Работа и мощность. Работой A, совершаемой постоянной силой Мощность — это работа за единицу времени (1 с):
Кинетическая и потенциальная энергия. Потенциальной энергией называется энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.
Потенциальная энергия упругих тел: Кинетическая энергия — энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта.
Скалярно умножим уравнение на перемещение частицы Если система замкнута, то есть внешние по отношению к системе силы отсутствуют, или равнодействующая всех сил равна нулю, то
Уравнение Бернулли. Уравнение Бернулли — для стабильно текущего потока (газа или жидкости) сумма кинетической и потенциальной энергии, давления на единицу объема является постоянной в любой точке этого потока.
Первое и второе слагаемое в Законе Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. А третье слагаемое в нашей формула является работой сил давления и не запасает какую-либо энергию. Из этого можно сделать вывод, что размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости или газа.Постоянная в правой части уравнения Бернулли называется полным давлением и зависит в общих случаях, только от линии потока.
Характеристики колебаний. Для описания колебательного движения существуют следующие характеристики: амплитуда, частота, период колебаний, циклическая частота. Модуль максимально в озможного смещения относительно положения равновесия называется амплитудой колебания А. Промежуток времени, в течение которого происходит одно полное колебание, называется периодом колебания Т. Измеряется в секундах. Число колебаний за одну секунду называется частотой
Циклическая частота
Гармонические колебания. Гармонические колебания — колебания, при которых физическая (или любая другая) величина изменяется с течением времени по синусоидальному или косинусоидальному закону. Кинематическое уравнение гармонических колебаний имеет вид
или
где х — смещение (отклонение) колеблющейся точки от положения равновесия в момент времени t; А — амплитуда колебаний, это величина, определяющая максимальное отклонение колеблющейся точки от положения равновесия; ω — циклическая частота, величина, показывающая число полных колебаний происходящих в течение 2π секунд; Обобщенное гармоническое колебание в дифференциальном виде
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1652; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.225.188 (0.007 с.) |

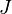 тела относительно произвольной оси равен сумме момента инерции этого тела
тела относительно произвольной оси равен сумме момента инерции этого тела  относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела
относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела  на квадрат расстояния
на квадрат расстояния 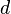 между осями:
между осями: 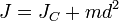 , где
, где
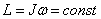 .
.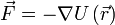 ,
, ,
,

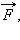 называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус углаα между векторами силы
называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус углаα между векторами силы  и перемещения
и перемещения 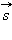 : A = F*s* cosα
: A = F*s* cosα
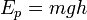
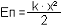
 (для твердого тела).
(для твердого тела).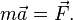
 . Учитывая, что
. Учитывая, что  , получим:
, получим: 
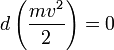 , а величина
, а величина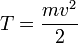 остаётся постоянной. Эта величина называется кинетической энергией частицы.
остаётся постоянной. Эта величина называется кинетической энергией частицы.

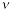 . Измеряется в герцах (Гц). Если частота равна 1 Гц, то это значит, что за одну секунду тело совершает одно колебание.
. Измеряется в герцах (Гц). Если частота равна 1 Гц, то это значит, что за одну секунду тело совершает одно колебание.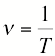
 - это величина на
- это величина на  больше частоты. Она показывает сколько колебаний совершается за
больше частоты. Она показывает сколько колебаний совершается за 

 ,
,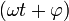 — полная фаза колебаний,
— полная фаза колебаний,  — начальная фаза колебаний.
— начальная фаза колебаний.



