
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение тела по наклонной плоскостиСодержание книги Поиск на нашем сайте
Динамика твердого тела Тело, деформациями которого в условиях рассматриваемой задачи можно пренебречь, называется абсолютно твердым телом. Всякое движение твердого тела можно разложить на два основных вида движения - поступательное и вращательное. Поступательное движение - движение, при котором любая прямая, проведенная через тело, остается параллельной сама себе (все точки тела описывают одинаковые траектории). Вращательное движение - движение при котором все точки тела движутся по окружностям, центры которых лежат на одной и той же прямой, называемой осью вращения. В самом общем случае тело может вращаться вокруг неподвижной точки, при этом его движение можно свести к трем независимым вращениям вокруг трех Момент инерции Момент инерции I тела зависит: а) от формы тела; в) от того, относительно какой оси вращается тело; б) от размеров тела; г) от распределения массы по объему тела. Наиболее простой случай, когда ось проходит через центр тяжести тела, тогда:
1. Момент инерции материальной точки массы m - 2. Момент инерции плоского тонкостенного цилиндра радиуса R массой m относительно его оси 3. Момент инерции сплошного цилиндра или диска 4. Момент инерции шар с ось проходящей через его центр 5. Момент инерции тонкий стержня с осью проходящей перпендикулярно через его середину 6. Момент инерции тонкий стержень, ось проходит через его конец Теорема Штейнера: Момент инерции тела I относительно произвольной оси равен сумме момента инерции этого тела I0 относительно оси, проходящей через центр инерции тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями
взаимно перпендикулярных осей, проходящих через эту точку.
Пусть твердое тело имеет неподвижную ось вращения, и к ней приложена произвольная сила Момент силы Моментом силы F относительно точки О называется физическая величина, определяемая векторным произведением радиус-вектора r, проведенного из точки О в точку приложения силы F. Направление M совпадает с направлением поступательного движения буравчика при его вращения от r к F.
где α – между векторами IV. Законы динамики вращательного движения. В основе динамики вращательного движения лежат законы Ньютона.
Опытной проверкой этого закона служит прибор – крестообразный маятник Обербека.
Согласно этому закону, два взаимодействующих тела всегда вращаются в разных направлениях относительно своих осей вращения. Закон сохранения момента импульса. В замкнутой системе момент внешних сил отсутствует т.е.
Закон сохранения момента импульса - момент импульса замкнутой системы относительно любой неподвижной точки не изменяется с течением времени.
Пример: Скамья Жуковского: скамья раскручена, и руки человека опущены. Человек расставляет руки с гантелями в стороны, скорость движения резко уменьшается. (Jω = const = mr2ω) → увеличение r приводит к уменьшению ω, чтобы произведение mr2ω оставалось постоянным. Кинетическая энергия вращающегося твёрдого тела. Кинетическая энергия твердого тела конечных размеров равна сумме кинетических энергий элементов, на которые разбито тело. Рассмотрим частный случай вращения твердого тела вокруг неподвижной оси. Кинетическая энергия каждого элемента, движущегося с линейной скоростью: Vi = ωri равна: Просуммировав по всем элементам, получим:
Если твердое тело одновременно участвует в двух движениях: поступательном со скоростью
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 394; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.14.12 (0.005 с.) |

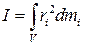

 .
.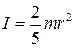
 .
.

 , лежащая в плоскости вращения.
, лежащая в плоскости вращения. ,
, 
 и
и 
 , прямо пропорционально моменту силы и обратно пропорционально моменту инерции тела:
, прямо пропорционально моменту силы и обратно пропорционально моменту инерции тела:
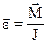 – основной закон динамики вращательного движения.
– основной закон динамики вращательного движения.




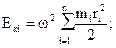
 – момент инерции тела, относительно оси вращения.
– момент инерции тела, относительно оси вращения.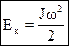 (11)
(11) и вращательном со скоростью
и вращательном со скоростью  , то
, то
 (12)
(12)



