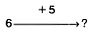Задачи на динамические отношения

Многочисленные отношения между объектами, возникающие в реальности, являются «динамическими отношениями» в том смысле, что они связывают ее последовательные, а не одновременные состояния. В математике о таких отношениях говорят как о последовательных трансформациях (преобразованиях во времени).
Общая модель такой последовательности трансформаций имеет вид:

Пример 1. В автобусе ехали 6 человек. На остановке вошли еще 5. Всего стало 11.

Пример 2. У мальчика было 7 фишек. В первой партии какой-то игры он выиграл 4 фишки, а во второй проиграл 3.

Умение решать различные задачи, связанные с последовательностью трансформаций, во многом зависит от способности ученика визуализировать всю последовательность событий на временной линии, а также обращать эту последовательность во времени (просмотр фильма от конца к началу).
Рассмотрим несколько задач этого типа.
Задача 1. В автобусе ехали 6 человек. На остановке в автобус вошли еще 5. Сколько всего человек стало в автобусе? Соответствующая схема:

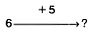
У большинства учащихся эта задача не вызывает больших трудностей, но обратная ей задача может вызвать определенные трудности у многих учеников.
Обратная задача 1. На остановке в автобус вошли 5 человек, и всего стало 11. Сколько человек ехали в автобусе вначале, до остановки?

Чтобы научить детей решать такие задачи, можно проделать следующие шаги:
1. Нарисовать на листе (доске) последовательные кадры событий фильма образов.

2. Прокрутить этот фильм в умственном плане.
3. Прокрутить фильм в обратном порядке, начиная от третьего кадра к первому. При этом решение задачи для детей становится очевидным. Дети обычно говорят: «Автобус едет задом наперед, на остановке люди выходят, значит, надо отнять (11–5), и остается в автобусе до остановки 6 человек».
4. Прокрутить фильм опять в прямом направлении, проверяя, так ли решена задача: «Ехали 6 человек, на остановке вошли еще 5, значит, надо прибавить. Шесть прибавить пять будет одиннадцать, как и в условии. Значит, решили правильно».
5. Перейти с помощью учителя к обобщенной схеме, например:

При этом важно попросить детей наложить рисунок из п. 1 на эту схему. На месте квадратиков как бы смутно будет виден образ автобуса, а посередине остановка и входящие в автобус люди. Такое наложение способствует переходу от частных задач к обобщенной задаче.
Затем необходимо прокрутить такой наложенный на схему фильм с автобусами в обратном порядке. Далее попросить детей придумать задачу, аналогичную задаче с автобусом. Рассмотреть вместе с детьми придуманные задачи, просматривая фильмы сквозь схему и определяя, соответствует ли придуманная задача этой схеме. Решить придуманные задачи.
6. Перейти к общей схеме:

Если раньше в задачах что-то добавлялось, то сейчас нужно придумать похожие задачи, в которых что-либо уменьшается. Решить эти задачи в соответствии с пп. 2, 3 и 4. Обратить внимание детей, что если в прямом фильме что-либо уменьшалось, то в обратном увеличивается на столько же (действие «сложение»).
7. Переход к пространственным трансформациям.
Спросить детей, может ли что-то изменяться, только уменьшаясь или увеличиваясь. Будут ли изменениями перемещения, повороты, растяжения и сжатия объектов? Обратить внимание на обратимость таких действий: поворот направо — поворот налево; подъем — спуск, движение вперед — движение назад и т.д.
Разобрать вместе с детьми, что для того, чтобы вернуться в исходное состояние, нужно выполнить обратное действие. Проделать это практически: стать, например, лицом к какой-либо стене (исходное состояние), повернуться направо под прямым углом (изменение или трансформация положения тела), оказавшись лицом к другой стене. Выполнить обратное изменение (поворот налево) и вернуться при этом в исходное положение.
Затем вспомнить все эти действия, прокрутив их В-К-фильм как в прямом, так и в обратном порядке. Придумать и разобрать вместе с детьми другие аналогичные задачи.
Можно порешать с детьми задачи на пространственные перемещения. Например: «Я стоял лицом к какой-то стене, затем повернулся под прямым углом налево и оказался лицом к окну. Как я стоял вначале?»
Обратить внимание детей, что задачи легче всего решаются, начиная с конца (аналитический способ), путем прокручивания фильма о совершенных действиях в обратном порядке.
Перед мысленным решением таких задач, возможно, некоторым детям нужно будет проделать все описанные в задаче действия практически. Желательно также, чтобы дети попробовали решать такие задачи, начиная от данных (синтетический метод), при этом они легко поймут, что сделать это очень трудно, так как требуется перебор очень большого числа различных вариантов.
По окончании цикла решения задач на трансформации вместе с детьми необходимо сделать вывод, что все такие задачи имеют одну общую визуальную схему:

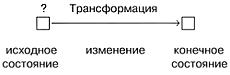
Для их решения нужно просмотреть фильм изменения состояний в обратном порядке, применяя при этом обратную трансформацию. Желательно также проделать аналогичную работу с задачами на две и более трансформации. Все они имеют общую схему:

для прямой задачи (по исходному состоянию и двум трансформациям определить конечное состояние)

и для обратной (по известным трансформациям и конечному состоянию определить начальное состояние).
Пример прямой задачи: В классе было 12 учеников. На перемене в класс вначале зашло еще 3 ученика, а затем вышло 5 учеников. Сколько учеников стало в классе?
Пример обратной задачи: Мальчик сыграл 2 партии в фишки. В первой он проиграл 6 фишек, а во второй выиграл 8. Всего у него осталось 10 фишек. Сколько фишек было у мальчика до игры?
Задачи на две (и более) трансформации решаются аналогично задачам с одной трансформацией. Важно уметь «сделать фильм» по задаче, а для обратной — прокрутить его в обратном порядке, применяя при этом обратные трансформации.
Желательно также, чтобы дети сами составляли по общей схеме аналогичные задачи, давая их друг другу для решения.

Статические задачи

В задачах этого типа изменений состояния объектов во времени не происходит. В таких задачах важно выделить объекты, связанные с ними величины и их меры, а также выявить все отношения (взаимосвязи) между ними и на основании этого определить неизвестные.
Рассмотрим следующую задачу.
Первая книга стоит 6 рублей, вторая на 7 рублей больше, а третья стоит столько же, сколько первая и вторая книги вместе. Сколько стоят три книги вместе?
Основной причиной трудностей при решении такой задачи является неумение визуально представить себе эту задачу, выделить объекты, величины и меры, а также увидеть отношения между известными и неизвестными.
Предлагаемая ниже последовательность действий при решении этой задачи позволяет преодолеть эти трудности (предполагается, что работа по формированию навыка визуализации с детьми уже проведена).
Этап 1. Осмысление или восприятие задачи
1. Попросить детей визуально представить объекты задачи. «О каких предметах говорится в задаче?» — «О книгах». — «Изобразите каждую на рисунке квадратом. Сколько таких книг?» — «Три».
Делается рисунок (первый раз учитель рисует на доске).
2. «Какие величины связаны с книгами?» — «Стоимость, или цена». — «Про какие книги известно, сколько они стоят?» — «Про первую». — «Поставим цену на рисунке».
3. «Что известно про стоимость второй и третьей книг?» — «Вторая стоит на 7 рублей больше». — «Изобразим взаимосвязь стоимостей второй и первой книг стрелкой, идущей от второй книги к первой. Над ней напишем, что про эту связь говорится в задаче».
4. Аналогично разбирается вся задача и составляется ее графическая схема, которая может иметь такой вид:

На этой схеме прямая стрелка указывает связи, фигурная — объединение, или сумму (слово «вместе» в задаче). Знак «?» соответствует вопросу задачи.
Пп. 1–4 относятся к этапу восприятия или осмысления задачи, в котором вычленяются объекты (книги) и отмечаются взаимоотношения величин, связанных с этими объектами, как с данными (известными), так и с величинами, которые нужно определить (неизвестными).
Построение визуальной схемы задачи позволяет ученику увидеть задачу как целостную единую структуру, создать ее ясный, целостно расчлененный образ, что, в свою очередь, создает умение «схватывать» задачу в целом, не теряя из виду всех ее данных.
Такое умение («схватывать») психологи и математики относят к одному из важных аспектов математической одаренности.
2-й этап. «Прочувствование» задачи
Этот этап тесно связан с информационными позициями НЛП и предполагает «вхождение в роль» каждого элемента задачи.
5. Графическая схема задачи рисуется на полу. Затем ученик поочередно входит в позицию каждой книги.
Будучи первой книгой, он говорит: «Моя стоимость 6 рублей», затем он переходит в позицию второй книги и смотрит, в соответствии со схемой, на первую книгу и говорит: «А я, вторая книга, стою на 7 рублей больше».
Затем вновь переходит по соединяющей стрелке в позицию первой книги и говорит: «А я, первая книга, стою на 7 рублей меньше».
Затем ученик выходит в третью позицию, или метапозицию, и мысленно отмечает взаимоотношение между стоимостями второй и первой книг. Затем ученик становится на фигурную скобку, объединяющую вторую и первую книги, делает объемлющий жест руками, представляет, как стоимости этих книг складываются, и говорит: «Вместе».
Затем он переходит в позицию третьей книги, проходит по стрелке, соединяющей третью книгу с фигурной скобкой, говоря при этом: «А я, третья книга, стою столько же, сколько вторая и первая вместе».
Затем ученик переходит в позицию фигурной скобки, соединяющей все три книги, делает объемлющий жест руками и, представляя себя знаком вопроса, говорит:
«Сколько же я, все три книги вместе, стою?» При этом ученик визуально и кинестетичеки представляет, что стоимости всех трех книг как бы объединяются в его теле.
6. Затем ученик осмысливает условие задачи, смотря на всю схему на полу и как бы оживляя в памяти свои визуальные образы и кинестетические ощущения. Здесь же важно попросить ученика повторить условие задачи. Если он не сможет этого сделать, вновь проделать этапы 1 и 2.
3-й этап. Составление плана решения
Здесь мы рассмотрим только аналитический метод (от вопроса к данным) как наиболее продуктивный.
7. Учитель на доске, а дети в тетради рисуют прямую линию, на которой будут отмечаться этапы решения. Далее учитель может сказать: «Дети, на этой линии — дороге, ведущей к нашей цели, решению задачи, — мы наметим отдельные шаги, которые приведут нас к этой цели, решению задачи, ответу на ее вопрос. Итак, какова наша цель, что мы должны узнать в задаче?» — «Наша цель — ответить на вопрос, сколько стоят три книги вместе».
На прямой линии справа ставится точка, обозначающая цель.

Учитель спрашивает: «Что мы должны знать, чтобы ответить на этот вопрос?» — «Сколько стоит каждая книга в отдельности». Учитель: «По условию, что мы об этом знаем?» — «Стоимость первой книги». — «А стоимость второй и третьей книг известна?» — «Нет». — «Следовательно, что мы должны узнать, чтобы ответить на вопрос задачи?» — «Мы должны узнать стоимость второй и третьей книг». — «Стоимость какой книги, второй или третьей, мы должны узнать раньше?» — «Второй».
Далее ставятся аналогичные необходимые вопросы и определяется нужная последовательность шагов. Получаем следующую временную линию шагов (последовательности) плана:

8. Пройти по позициям схемы задачи (на полу или мысленно в тетради) в соответствии с пунктами плана, начиная от цели — вопроса задачи. Фигурная скобка с вопросом, далее стрелка от третьей книги к фигурной скобке, объединяющей первую и вторую книги, далее по стрелке от второй книги к первой.
9. Ученик затем проходит по схеме в обратном порядке, начиная от первой книги, к фигурной скобке с вопросом задачи и соотносит эти шаги с этапами на временной линии, мысленно намечая свои действия по реализации плана. При этом он может вслух комментировать свои будущие действия по решению задачи.
Это может примерно выглядеть следующим образом: «К 6 прибавлю 7, узнаю стоимость 2-й книги». Став в позицию фигурной скобки, объединяющей 1-ю и 2-ю книги: «Сложу стоимости 1-й и 2-й книг», далее, проходя от этой фигурной скобки по связывающей стрелке к 3-й книге: «Получу стоимость 3-й книги». Став в позицию фигурной скобки с вопросом задачи: «Сложу стоимости всех трех книг, ответив на вопрос задачи». (При этом дети с очевидностью осознают. что достаточно только прибавить стоимость 3-й книги к уже вычисленной ранее сумме стоимостей 1-й и 2-й книг.)
4-й этап. Реализация плана
10. На этом этапе оформляются соответствующие записи в тетради. Порядок записи действий соответствует порядку, выявленному в п. 8 (от начала к концу). Этот этап обычно не вызывает затруднений у детей, если правильно проделаны предыдущие этапы.
Выполнение описанных выше действий при решении задачи позволяет включить в процесс решения все модальности: визуальную, кинестетическую и аудиальную, а также обеспечить гармоничную работу левого и правого полушарий головного мозга.
Естественно, что такой алгоритм достаточно выполнить вначале на нескольких задачах, в дальнейшем его можно проделывать мысленно, а со временем он «свернется» и перейдет в подсознательную область, став автоматическим навыком.