

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Сложение чисел с переходом через десяток
7 + 5 =? Успешные ученики мысленно разбивают число 5 на 3 и 2, 3 добавляют к 7, получают 10 и к 10 добавляют 2, получая 12.
Обычно вначале такие действия делаются учителем на доске (а детьми в тетради), и многие ученики запоминают процесс этих действий в виде фильма, который в дальнейшем может «свернуться» и перейти в подсознательную область.
Для учеников, которым трудно даются такие примеры, необходима работа по сознательному созданию нужного
мысленного фильма. Это можно сделать следующим образом.
В тетради (или на доске) ученик пишет: 7 + 5. Вопрос учителя: «На какие числа можно разбить число 5, чтобы тебе было легче посчитать?» Если ученик затрудняется, подсказать: «К семи прибавить три — ты уже легко считаешь. Сколько это будет? (Обычно это не вызывает затруднений.) Если мы взяли от пяти три, сколько останется? (Два.)». Делается запись:  . Сложи 7 и 3. . Сложи 7 и 3.
Делается запись: 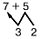
Далее: (7 + 3) + 2, 10 + 2 = 12. Попросить ребенка вспомнить (воспроизвести в умственном плане) весь фильм и озвучить его: «Разбиваем 5 на 3 и 2, тройка идет к семерке, будет 10, и остается еще 2, всего будет 12». Записать пример полностью: 7 + 5 = 12.
Дать еще несколько примеров, вначале с записью фильма в тетради, затем с созданием такого фильма сразу в уме. Как и ранее, отслеживать и направлять движение глаз вверх.
Сложение чисел
В математике сложению двух чисел соответствует объединение двух непересекающихся множеств. Так, поверхностной структуре 2 + 4 = 6 соответствует глубинная структура, которая может быть представлена в памяти в виде следующего В, К, Д-фильма: «Вижу два предмета — объект № 1, рядом справа — четыре предмета — объект № 2» (первый кадр). «Далее объект № 2 двигается к объекту № 1, при этом возникает кинестетическое ощущение в правой руке, и я вижу, как она перемещает объект № 2, при этом произношу про себя: «Соединяю» (второй кадр).
«Далее предметы соединяются, образуя один объект» (третий кадр). Затем идет подсчет предметов: «Вижу и чувствую свою руку, последовательно указывающую на объединенные предметы (одновременно взгляд фокусируется на этих предметах), при этом произношу соответствующие числа: «Один, два, три, четыре, пять, шесть», делая на последнем предмете жест, объемлющий всю группу предметов, и говоря: «Всего шесть» (четвертый кадр).
Схематично этот фильм можно изобразить следующим образом:

На данной схеме овал соответствует границе поля внимания, выделяющего предметы, черные кружки — каким-либо предметам.
Очевидно, чтобы научить ребенка действию сложения двух чисел, необходимо начинать с действий с реальными предметами, затем переходить к созданию в памяти соответствующего В, К, Д-фильма (глубинной структуре) и затем к поверхностной, в данном примере 2 + 4 = 6, или словами: «К двум прибавить четыре получится шесть». Для более глубокого освоения действия сложения необходимо давать и обратные задания — перейти от поверхностной структуры, заданной с помощью математических знаков и слов, вначале к глубинной структуре (рассказать о соответствующем фильме в голове), а затем и к выполнению реальных действий с предметами.
Очевидно, что выполнение действий с предметами в обратном порядке и создание соответствующей глубинной структуры (прокручивание фильма в обратном порядке) соответствует действию вычитания чисел.
Обобщенный алгоритм обучения детей арифметическим действиям сложения и вычитания может иметь следующий вид.
1. «Установка на киносъемку» В, К, Д-фильма о собственных действиях с предметами (осознание своих действий).
2. Действия с реальными предметами и словесное их комментирование, вначале вслух, затем шепотом, затем про себя.
3. Вспоминание и рассказывание глубинной структуры (или В, К, Д-фильма). Если не вспоминается правильно, вновь проделать пункт 2.
4. Проговаривание и запись поверхностной структуры с помощью математических знаков и слов устной и письменной речи.
5. Обратный процесс — переход от поверхностной структуры примера к рассказыванию глубинной структуры (или В, К, Д-фильма) примера и затем к действию с реальными предметами.
Важно отметить следующее. Если в приведенном выше примере двигать объект № 1 к объекту № 2 (слева направо), то соответствующая математическая запись будет иметь другой вид: 4 + 2 = 6 (к четырем прибавить два). Поэтому желательно варьировать порядок действий с предметами, обращая внимание ученика на изменения как в В, К, Д-фильме, так и в соответствующей ему математической и словесной записи.
Вначале, возможно, для ученика потребуется образец в виде предметных действий самого учителя, затем совместные действия и в конце самостоятельные действия ученика (но начинать с действий самого ребенка!).
Вычитание чисел
В методической литературе по математике отмечается, что значительная часть учащихся при выполнении предметных действий, связанных с вычитанием, фиксируют скорее пространственное отделение, разъединение двух множеств, чем вычленение и удаление части из целого, что затрудняет усвоение и понимание ими смысла решения примеров типа 8 — 2 = 6.
Происхождение различных ошибок при освоении понятия вычитания путем выполнения предметных действий объясняется так: «В психологии установлено, что дошкольникам свойственно не удерживать одновременно во внимании целое и его части: когда они оперируют частями, то уже не видят перед собой целого, и наоборот. Преодоление этих ошибок происходит постепенно и обычно в возрасте 7–8 лет. Поэтому так важно продумать психологический аспект изучения этого вопроса» (Истомина, с. 40).
Я думаю, что осознание глубинной структуры действия вычитания поможет прояснению этого психологического аспекта. Рассмотрим, как я сам осознаю свою глубинную структуру (для такого самоосознания необходимо сильно замедлить «прокрутку» фильма глубинной структуры).
Когда я решаю пример 8 – 2 =, происходит примерно следующее:
 1. Я выделяю взглядом число 8. 1. Я выделяю взглядом число 8.
2. Создается в уме первый кадр — 8 предметов.
3. Произношу в уме «восемь».
4. Выделяю взглядом – 2. 1-й кадр
5. Создается в уме второй кадр, как бы проводится линия, отделяющая два предмета от общей группы.

6. «Кусок» с двумя предметами отодвигается в сторону. Произношу в уме «вычесть».

7. Пересчитываются оставшиеся предметы (6).

8. Я вижу в уме все четыре кадра рядом, в едином поле зрения:

Смотрю на них слева направо и озвучиваю: «Восемь (1-й кадр) вычесть два (2-й и 3-й кадры) будет шесть (4-й кадр)».
9. Записываю в виде ответа 8 – 2 = 6 и проговариваю про себя или вслух.
Очевидно, что если весь этот процесс (фильм) свернуть во времени, то кадры наложатся в умственном плане друг на друга, что, по сути дела, и означает одновременное удержание во внимании целого и части.
Практика коррекционной работы с детьми показала, что выполнение предметных действий с одновременным созданием и запоминанием глубинной структуры по описанному алгоритму устраняет трудности в понимании действия вычитания у «слабых» учащихся.
Легко видеть, что прокручивание описанного выше фильма в обратном порядке приводит к поверхностной структуре 6 + 2 = 8, что делает очевидным взаимообратный характер операций сложения и вычитания.
У меня не вызывает сомнения, что изучение этих, как и всех других взаимообратных операций, должно происходить одновременно, так как для них используется практически одна и та же глубинная структура (фильм, просматриваемый в прямом или в обратном порядке).
Устный счет
Устный счет лучше всего выполняют люди с хорошей визуальной памятью. Алгоритм формирования навыка устного счета может быть примерно следующим.
1. Ученик выполняет действия на бумаге, как бы снимая В, К, Д-фильм о своих действиях, и заносит его в память. При этом он комментирует свои действия вслух и про себя.
2. Воспроизводит фильм в уме, рассказывая о своих образах. Если на каком-то этапе фильма возникает ошибка, то необходимо вновь вернуться к шагу 1.
3. Попробовать выполнить действия с числами в уме, сразу создавая нужные образы фильма и комментируя их с помощью речи. Если не получается, то необходимо выполнять шаги 1 и 2 до формирования нужного навыка (возможно, в другое время).
4. Затем можно усложнять примеры, увеличивая число цифр.
|



 . Сложи 7 и 3.
. Сложи 7 и 3.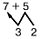

 1. Я выделяю взглядом число 8.
1. Я выделяю взглядом число 8.






