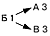Задачи на родственные отношения

Решение задач этого типа с помощью составления их графических схем и их В, А, К, Д-«прочувствования» способствует развитию у детей математического мышления, более четкому и ясному пониманию таких важных понятий, как отношение (или взаимосвязь) объектов, структура целой сети отношений, их уровни, что в конечном счете ведет к развитию целостного, системного мышления.
Кратко рассмотрим следующую задачу: «На лавочке сидели: бабушка, две мамы, две дочки и внучка (для мальчиков лучше задача с дедушкой, отцами и внуком), всего три человека. Как это может быть?»
Вначале у детей складывается впечатление, что всего должно быть шесть человек. Но составление графической схемы делает понимание этого кажущегося парадокса очевидным.

На схеме буквы Д, М, В и Б обозначают отношения: дочка, мама, внучка и бабушка. Эту схему можно нарисовать на полу и затем пройти по ней, прочувствовав все отношения (лучше использовать на схеме имена собственных родных).
Находясь в позиции 1, ученик смотрит на позицию 2 (маму) и говорит: «Она моя мама», далее смотрит на позицию 3 и говорит: «Она моя бабушка». Далее он (она) переходит в позицию 2 (мамы), смотрит вниз на позицию 1 и говорит: «Она (имя) моя дочка». Затем поворачивается и смотрит на позицию 3, говоря: «Она (имя) моя мама». Из позиции 3 ученик смотрит вначале на позицию 2, говоря: «Она (имя) моя дочка», а затем на позицию 1, говоря: «Она (имя) моя внучка». (Вот тут-то у большинства детей возникает ясное понимание, что их бабушка — это мама их мамы!)
Затем ученик выходит в метапозицию (взгляд со стороны) и еще раз анализирует схему и соответствующие ей родственные отношения. Находясь в позиции мамы (как бы играя ее роль), ученик вспоминает как можно больше того, что связано с этим понятием (роды, вскармливание, уход, воспитание и т.д.).
Затем детям можно предложить самим придумать похожую задачу на родственные отношения по следующей схеме:

Позиции 1, 2 и 3 соответствуют предыдущей схеме. Ими могут быть, например, дедушка, папа и внук. Кто же может быть в позиции 4, на том же уровне, что и позиция 2? Если дети не догадаются, подсказать, что это, например, тоже сын дедушки, родной брат папы (или дочь дедушки и сестра папы и т.д.).
Задача может быть сформулирована следующим образом: «В комнате находились дедушка, внук, два отца и три сына, всего четыре человека. Как это может быть?»
При прохождении всех четырех позиций добавится еще и понимание родственных отношений племянник (племянница) — дядя (тетя).
После проработки ряда задач этого типа можно предложить детям составить вместе с родителями схему родственных отношений своей семьи и проработать ее, как описано выше.

Задачи "Ходы конем"

Задачи этого типа направлены на развитие способностей детей к действиям в умственном плане с образами и представлениями и мысленного планирования. В них развивается способность переключать ход мысли с прямого направления на обратное и решать задачу, начиная с цели (требования задачи).
Решение задач этого типа рассмотрим на примере девятиклеточного поля.

	A	Б	В

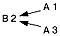
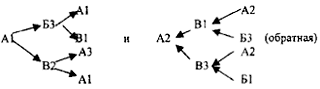
Каждая клетка поля имеет свое название, которое состоит из буквы и цифры. Например, нижняя клетка слева — А 1, в центре поля — Б 2 и т.д. Шахматная фигура «конь» может ходить только буквой «Г»: две клетки по прямой и одну в сторону.
В задачах этого типа требуется определить:
1. Куда может попасть конь, сделав только один ход из какой-либо клетки.
2. Откуда может прийти конь, если он, сделав только один ход, оказался на определенной клетке (обратная задача).
3. Тот же вопрос, но конь может сделать два хода (и более).
4. Двухходовые задачи, в которых нужно определить промежуточную клетку, на которую должен пойти конь, чтобы оказаться в какой-то конечной клетке.

Пример задачи 1-го вида
Конь находится на клетке Б 1. Куда он может сделать ходы? (На клетки А 3 и В 3.)

Соответствующая запись:

Пример задачи 2-го вида
Где ранее находился конь, если, сделав один ход, он оказался на клетке В 2?
(На клетке А 1 или А 3.)

Соответствующая запись имеет вид:

Пример задачи 3-го вида

Пример задачи 4-го вида

Освоение задач этого типа предполагает четыре постепенно усложняющихся этапа.
1. Выполнение ходов учениками на игровом поле в тетради с помощью пальца или карандаша.
2. «Прошагивание» ходов на игровом поле на полу.
3. Выполнение ходов мысленно, ориентируясь на игровое поле, нарисованное на доске.
4. Выполнение ходов (мысленное решение задачи) без опоры на внешнее поле.
При решении обратных задач необходимо начинать с действенного и мысленного «прокручивания фильма» о ходах коня в обратном порядке. Например, ученик может сделать два шага вперед и шаг в сторону на реальные или представляемые клетки на полу, а затем вернуться в исходную позицию, сделав шаг в сторону, противоположную прямому ходу, и два шага назад, вернувшись в начальную позицию коня. Затем он должен перейти в метапозицию и мысленно представить прямой и обратный ходы коня.
Решение задач на нахождение промежуточных клеток предполагает сочетание проб от начальной клетки в прямом направлении и с конечной клетки в обратном направлении (обратные ходы) и нахождение как бы их «пересечения».
После освоения решения задач на девятиклеточном поле можно предложить детям попробовать свои силы и на 16-клеточном (и более). Естественно, при этом задачи значительно усложняются и могут быть недоступны для «слабых» учеников.