Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ротор векторного поля. Формула СтоксаСодержание книги
Поиск на нашем сайте Ротор — векторная характеристика вихревой составляющей векторного поля. Это вектор с координатами:
Потенциальные поля. Условие потенциальности поля. Потенциальное (или безвихревое) векторное поле в математике — векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трёхмерном пространстве является равенство нулю ротора поля. В физике, имеющей дело с силовыми полями, математическое условие потенциальности силового поля можно представить как требование равенства нулю работы при перемещении частицы, на которую действует поле, по замкнутому контуру. В качестве потенциала поля в этом случае можно выбрать работу по перемещению пробной частицы из некоторой произвольно выбранной исходной точки в заданную точку (по определению эта работа не зависит от пути перемещения). Например, потенциальными являются статическое электрическое поле, а также гравитационное поле в ньютоновой теории гравитации. Соленоидальные поля. Условие соленоидальности. Векторное поле называется соленоидальным, если через любую замкнутую поверхность S его поток равен нулю:
Если это условие выполняется для любых подобластей некоторой области W, то это условие равносильно тому, что равна нулю дивергенция векторного поля
Лапласово поле. Уравнение Лапласа.
Криволинейные ортогональные координаты В евклидовом пространстве особое значение имеет использование ортогональных криволинейных координат, поскольку формулы, имеющие отношение к длине и углам, выглядят в ортогональных координатах проще, нежели в общем случае. Что связано с тем, что метрическая матрица в системах с ортонормированным базисом будет диагональной, что существенно упростит расчёты. Коэффициенты Ламэ. Элементы длины кривой, площади поверхности, объема Коэффициенты Ламе Выпишем дифференциал дуги в криволинейных координатах в виде (используется правило суммирования Эйнштейна):
Принимая во внимание ортогональность систем координат (
где
Положительные величины Тензор римановой метрики, записанный в координатах qi, представляет из себя диагональную матрицу, на диагонали которой стоя́т квадраты коэффициентов Ламе:
Градиент, дивергенция и ротор в криволинейных координатах Градиент
где Hi — коэффициенты Ламе. Дивергенция
Градиент, дивергенция и ротор в сферических координатах Градиент Коэффициенты Ламе:
Отсюда:
Дивергенция Коэффициенты Ламе:
Отсюда:
Ротор
где Hi — коэффициенты Ламе. Градиент, дивергенция и ротор в цилиндрических координатах Градиент Коэффициенты Ламе:
Отсюда:
Дивергенция Коэффициенты Ламе:
Отсюда:
Оператор Лапласа в криволинейных координатах Опера́тор Лапла́са (лапласиа́н, оператор дельта) — дифференциальный оператор, действующий в линейном пространстве гладких функций и обозначаемый символом . Функции . Функции  он ставит в соответствие функцию он ставит в соответствие функцию  . . Оператор Лапласа эквивалентен последовательному взятию операций градиента и дивергенции: В произвольных ортогональных криволинейных координатах в трехмерном пространстве
где Аффинное пространство Аффинное пространство — служит обобщением аффинных свойств евклидова пространства. Во многом схоже с векторным пространством, но в отличие от последнего, точки в аффинном пространстве являются равноправными. В частности в аффинном пространстве нет понятия нулевой точки или начала отсчёта. В аффинном пространстве возможно вычитать друг из друга точки и получать векторы так называемого присоединенного пространства; также возможно прибавлять вектор к точке и получать другую точку, но нельзя складывать точки друг с другом Определение Аффинное пространство над полем Если поле § Элементы A называются точками аффинного пространства § Пространство V называется пространством присоединенным к A § Образ действия § Для двух точек § Размерность пространства A определяется равной размерности присоединенного пространства V. 28. Преобразования базиса 29. Ковариантный тензор 30. Контрвариантный тензор
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1498; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.008 с.) |

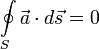
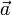
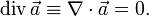

 при
при  ) это выражение можно переписать в виде
) это выражение можно переписать в виде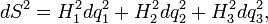

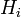 , зависящие от точки пространства, именуются коэффициентами Ламе или масштабными коэффициентами. Коэффициенты Ламе показывают, сколько единиц длины содержится в единице координат данной точки и используются для преобразования векторов при переходе от одной системы координат к другой.
, зависящие от точки пространства, именуются коэффициентами Ламе или масштабными коэффициентами. Коэффициенты Ламе показывают, сколько единиц длины содержится в единице координат данной точки и используются для преобразования векторов при переходе от одной системы координат к другой.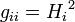 gij = 0 для i ≠ j
gij = 0 для i ≠ j



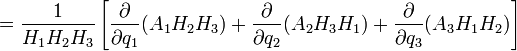 , где Hi — коэффициенты Ламе.
, где Hi — коэффициенты Ламе. .
.
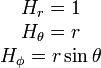 .
.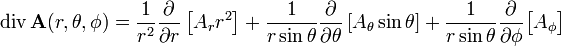

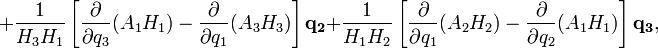
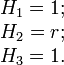

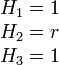 .
.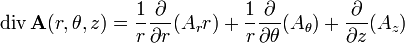
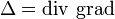 , таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля
, таким образом, значение оператора Лапласа в точке может быть истолковано как плотность источников (стоков) потенциального векторного поля  в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом
в этой точке. В декартовой системе координат оператор Лапласа часто обозначается следующим образом  , то есть в виде скалярного произведения оператора набла на себя.
, то есть в виде скалярного произведения оператора набла на себя. :
: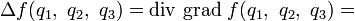

 — множество A со свободным транзитивным действием аддитивной группывекторного пространства V над полем
— множество A со свободным транзитивным действием аддитивной группывекторного пространства V над полем 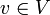 на
на 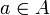 обозначается a + v
обозначается a + v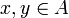 через
через  обозначается такой вектор из V, что
обозначается такой вектор из V, что