
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оператор Гамильтона (набла-оператор). Правила работы с нимСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Опера́тор на́бла (оператор Гамильтона) — векторный дифференциальный оператор, обозначаемый символом
Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div (дивергенция), rot (ротор), а также оператор Лапласа Векторные поля. Векторные линии. Поток векторного поля Векторное поле — это отображение, которое каждой точке рассматриваемого пространства ставит в соответствие вектор с началом в этой точке. Например вектор скорости ветра в данный момент времени изменяется от точки к точке и может быть описан векторным полем. Для евклидова пространства векторное поле, заданное на евклидовом пространстве, соответствует полю направлений, где каждой точке пространства сопоставляется некоторая прямая, проходящая через данную точку. Точка пространства, в которой векторное поле равно нулю, называется особой точкой векторного поля, в ней направление не определено. Циркуляция — интеграл по замкнутому контуру:
Поток векторного поля
Векторное поле, дивергенция которого всюду равна нулю, называется соленоидальным; оно может быть представлено как ротор некоторого другого векторного поля.
Векторное поле, ротор которого равен нулю в любой точке, называется потенциальным (безвихревым); оно может быть представлено как градиент некоторого скалярного поля (потенциала). Дивергенция векторного поля. Формула Остроградского Дивергенция (от лат. divergere — обнаруживать расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть операция дифференцирования, в результате применения которой к векторному полю получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле» (точнее — насколько расходятся входящий и исходящий поток).
Если учесть, что потоку можно приписать алгебраический знак, то нет необходимости учитывать входящий и исходящий потоки по отдельности, всё будет автоматически учтено при суммировании с учетом знака. Поэтому можно дать более короткое определение дивергенции: дивергенция — это дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность малой окрестности каждой внутренней точки области определения поля. Оператор дивергенции к полю F: divF Определение дивергенции выглядит так:
где ФF — поток векторного поля F через сферическую поверхность площадью S, ограничивающую объём V. Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S и объёмом V допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю (то есть чтобы вся поверхность находилась в бесконечно малой окрестности данной точки, что нужно, чтобы дивергенция была локальной операцией и для чего очевидно недостаточно стремления к нулю площади поверхности и объема ее внутренности). В обоих случаях подразумевается, что
Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трёхмерном декартовом пространстве дивергенция будет определяться выражением
С точки зрения физики, дивергенция векторного поля является показателем того, в какой степени данная точка пространства является источником или стоком этого поля:
|
|||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 470; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.12.244 (0.01 с.) |

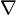 Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом:
Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом: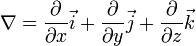
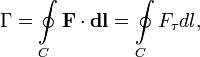
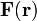 через поверхность S определяется как интеграл по S:
через поверхность S определяется как интеграл по S: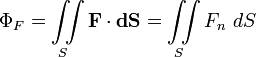 где Fn — проекция вектора поля на нормаль к поверхности, dS — «векторный элемент поверхности», определяемый, как вектор единичной нормали, умноженный на dS. Простейшим примером этой конструкции является объём жидкости, проходящий через поверхность S, при её течении со скоростью F.
где Fn — проекция вектора поля на нормаль к поверхности, dS — «векторный элемент поверхности», определяемый, как вектор единичной нормали, умноженный на dS. Простейшим примером этой конструкции является объём жидкости, проходящий через поверхность S, при её течении со скоростью F.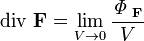
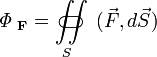
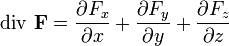
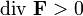 — точка поля является источником;
— точка поля является источником;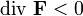 — точка поля является стоком;
— точка поля является стоком;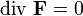 — стоков и источников нет, либо они компенсируют друг друга.
— стоков и источников нет, либо они компенсируют друг друга.


