
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи с использованием строкового типа данных.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В этом классе задач приходится оперировать таким типом данных, как строки, проводить преобразования строковых данных в числовые и наоборот. Задача 3.1 Для заданной строки символов проверить, является ли она симметричной или нет. (Симметричной считается строка, которая одинаково читается слева направо и справа налево). Задача 3.2 Для заданной строки символов проверить, является ли она палиндромом (симметричной с точностью до пробелов) или нет. Задача 3.3 Для заданной строки символов определить сумму всех входящих в неё цифр. Задача 3.4 Для заданной строки символов вычислить произведение входящих в эту строку целых чисел (без учета их знаков). Например, для строки "kjjjkkj 2. 5 jkjn,,,hfd 45 jgfvjlkfdii 10, 2 hfhg" произведение 2*5*45*10*2=9000. Задача 3.5 Для заданной строки символов вычислить сумму входящих в неё цифр, причем знак очередного слагаемого должен быть противоположным знаку предыдущего слагаемого. Задача 3.6 Для заданной строки символов найти наибольшее записанное в этой строке целое число (без учета знака числа). Например, для строки "sdfvgsd1.9fdmjgvb-15.2dnj05" наибольшее целое число 15. Задача 3.7 Для заданной строки определить все входящие в неё символы. Например: строка "abccbbbabba" состоит из символов "a","b" и "с". Задача 3.8 Задана строка символов. Среди литер этого текста особую роль играет знак #, появление которого означает отмену предыдущей литеры текста; k знаков # отменяют k предыдущих литер (если такие есть) Напечатать строку с учетом роли знака #. Например, строка "VR#Y##HELO#LO" должна быть напечатана в виде: "HELLO". Задача 3.9 Задана строка символов. Определить, какой символ встречается в этой строке подряд наибольшее число раз. В ответе указать символ, образующий самую длинную последовательность, длину последовательности и номер символа, с которого она начинается. Задача 3.10 Для заданной строки символов, состоящей из строчных букв и пробелов, определить слово наибольшей длины, которое начинается и заканчивается на одну и ту же букву. Например: строка - "револьвер системы наган", слово - "револьвер".
Задача 3.11 В символьной строке имеются круглые скобки. Проверить, правильно ли они расставлены. Задача 3.12 Заданы две строки. Определить, являются ли они анаграммами, то есть одна строка получена из другой перестановкой букв. Задача 3.13 Вспомним игру: "Придумай слово", в которой из букв слова-донора составляют другие слова. Например, из слова МОНИТОР можно получить МОТОР, РОТ, ТИР и др. Вхождение каждой буквы в новое слово допускается не более того числа раз, с каким она входит в слово-донор. Задача 3.14 Задана строка символов, содержащая два или более слов, разделенных пробелами. Написать программу, меняющую местами все четные и нечетные слова в строке, предполагая, что за один раз можно менять местами не более двух символов. Решения задач Задача 3.1 Проще всего в этой задаче определить длину строки n, организовать цикл по номеру символа в строке и сравнивать попарно первый символ с последним, второй - с предпоследним и т.д. Если хотя бы одна пара различна, то строка не симметричная. Так как просматривается сразу пара символов, то в цикле будет m = n div 2 повторений. Для запоминания результата просмотра введем переменную k (k будет равна 0, если строка симметрична и 1 иначе). Задача 3.2 Если удалить из заданной строки все пробелы, то задача сведется к предыдущей. Задача 3.3 Так как все цифры от 0 до 9 располагаются в таблице кодировки компьютера подряд, то проще всего проверить, является ли символ s[i] цифрой, можно с помощью неравенства '0'<=s[i]<='9' (на Паскале (s[i]>='0')and(s[i]<='9')). Для преобразования строки в число в Паскале используется процедура val(s,v,k), где s - строка (или символ), v - переменная числового типа, куда будет занесён результат преобразования, k - переменная целочисленного типа, которая принимает значение 0, если преобразование строки в число прошло успешно.
Задача 3.4 Пусть s - строка. Обозначим длину строки - l. Организуем цикл, в котором будем проверять, является ли очередной символ цифрой, если да, то организуем новый цикл, в котором будем формировать строку sn, состоящую из цифр (очередное целое число). Потом преобразуем sn в число и вычислим произведение. Программа на Паскале, реализующая данный алгоритм, будет иметь следующий вид (переменная p в этой программе используется для накапливания значения произведения, переменная kod - для хранения кода результата преобразования строки в число): var sn,s:string; l,k,kod:integer; v,p:real;begin writeln('Введите строку'); readln(s); l:=length(s); p:=1; k:=1; repeat sn:=''; while (s[k]>='0')and(s[k]<='9')and(k<=l) do begin sn:=sn+s[k]; k:=k+1; end; if sn<>'' then begin val(sn,v,kod); p:=p*v; end; k:=k+1; until k>l; writeln(' p=',p);end.Задача 3.8 Обозначим s - исходную строку, l - длину этой строки. Для решения создадим ещё одну строку s1(вначале пустую). Далее организуем цикл по номеру символа в строке s. Если очередной символ не #, то добавим его к строке s1, если это знак # и строка s1 не пустая, то удалим из неё последний символ. Задача 3.10 Пусть s - заданная строка. Для решения данной задачи определим длину строки l и организуем цикл по номеру символа i. Символ строки является первым символом некоторого слова в том случае, когда он сам не является пробелом, и либо он - первый символ строки, либо слева от него стоит пробел. Если мы нашли первый символ некоторого слова, то запомним его номер и организуем цикл, в котором найдем номер последнего символа этого слова (символ будет последним в слове либо тогда, когда после него стоит пробел, либо когда он последний символ строки). Если последний символ слова совпадает с первым символом этого слова, и длина слова наибольшая из всех найденных, запомним эту длину и номер первого символа этого слова. Задача 3.11 Обозначим K - число левых скобок, M - число правых скобок, тогда, на каждом шаге подсчета скобок, должно выполняться условие: K>=M. После подсчета всех скобок должно выполниться условие K=M. Задача 3.14 Имеется несколько путей решения этой задачи. Для упрощения предположим, что строка не начинается и не заканчивается пробелом и что между словами в строке стоит ровно по одному пробелу. Пусть известна пара слов, которую необходимо переставить, и - номера первой и последней букв в первом слове, и - номера первой и последней букв во втором слове. Рассмотрим способ, в котором для перестановки слов будем использовать следующий алгоритм:
Задачи повышенной сложности Задача 4.1
Задача 4.2 Вывести на экран цифры числа 31000. Если попытаться получить число непосредственно умножением, компьютер выдаст сообщение об ошибке. Задача 4.3 Написать программу для умножения двух чисел, количество цифр в каждом из которых может достигать 100. Например, для умножения вида: Задача 4.4 Сообщество роботов живет по следующим законам: один раз в год они объединяются в полностью укомплектованные группы по 3 или 5 роботов (причем число групп из 3 роботов - максимально возможное). За год группа из 3 роботов собирает 5, а группа из 5 - 9 новых собратьев. Каждый робот живет 3 года после сборки. Известно начальное количество роботов (К>7), все они только что собраны. Определить сколько роботов будет через N лет. Задача 4.5 На квадратном клетчатом листе бумаги 8x8 клеток заштрихована часть клеток (пример на рисунке). Определить вписанный в решётку прямоугольник максимальной площади, не содержащий заштрихованных клеток. В качестве ответа вывести площадь прямоугольника и координаты его двух противоположных вершин. (Предполагается, что прямоугольник с максимальной площадью один.)
Задача 4.6 На квадратном клетчатом листе бумаги n на m клеток нарисовано несколько фигур, каждая из которых состоит только из целых клеток. Различные фигуры не накладываются и не соприкасаются (пример на рисунке). Определить фигуру максимальной площади. (В качестве ответа вывести площадь фигуры и координаты одной из её точек. Предполагается, что фигура с максимальной площадью одна.) Задача 4.7 Подсчитайте количество одно-, двух-, трёх- и четырехпалубных кораблей, расположенных на поле для игры "Морской бой". Корабли не могут быть изогнутыми и друг с другом не соприкасаются. Поле для игры задается в виде таблицы 10x10, каждый элемент которой равен либо 0, если клетка свободна, либо 1, если занята. Задача 4.8 Лабиринт задан в виде матрицы размером n на m. Стенам лабиринта соответствуют единицы, проходам - нули. Определить, можно ли из точки с координатами (i 1, j 1) попасть в точку с координатами (i 2, j 2). Для усложнения задачи можно предложить указать самый короткий путь из заданной точки, причем из всех путей одинаковой длины выбирать путь с наименьшим числом поворотов. Задача 4.9 На рисунке изображен треугольник из чисел. Вычислите наибольшую сумму чисел, расположенных на пути, начинающемся в верхней точке треугольника и заканчивающемся на его основании. Каждый шаг на пути может идти вниз по диагонали влево или вниз по диагонали вправо. Число строк в треугольнике больше1 и не больше100. Треугольник составлен из целых чисел от 0 до 99. Задача 4.10 Имеется n населенных пунктов, пронумерованных от 1 до n. Некоторые пары пунктов соединены дорогами (в том числе дорогами с односторонним движением). Определить, можно ли попасть по этим дорогам из одного заданного пункта в другой. (Для усложнения задачи можно предложить указать все возможные пути без петель и тупиков из одного пункта в другой). Задача 4.11 Заданы две фразы. Определить наибольшую последовательность отличных от пробелов символов, входящую в обе фразы в одном и том же порядке. Например, в предложениях: Задача 4.12 В морском порту города Владивостока хранятся N контейнеров (N - чётное число). Для погрузки контейнеров на судно, чтобы обеспечить равномерную загрузку, их необходимо разделить на две половины так, чтобы их массы были максимально близки. Решить эту задачу, предполагая, что информация о массах контейнеров (в тоннах) хранится в массиве M(N). В качестве ответа указать номера контейнеров одной половины и получаемые массы для каждой из половин.
Задача 4.13 На шахматной доске необходимо расставить 8 ферзей так, чтобы они не угрожали друг другу. Задача 4.14 На шахматной доске размером 4x4 клетки расставить 4 ладьи так, чтобы они не угрожали друг другу. Определить все такие расстановки (всего их будет 24). Решения задач Задача 4.2 Для записи больших чисел удобно использовать массивы, записывая цифры числа как элементы массива. Оценим количество цифр, необходимых для записи 31000: end. Здесь stp - степень, в которую возводится число 3, a[500] - массив, в котором хранятся цифры полученного числа, prn - перенос из разряда в разряд. Объём вычислений в данной программе можно значительно сократить, если каждый раз умножать на 3 не весь массив a, а только его занятую часть. Задача 4.3 Принцип решения этой задачи такой же, как и у предыдущей. Результат умножения двух стозначных чисел будет не превышать по размеру 200 знаков (т.е. для хранения результата понадобится массив из 200 элементов). Для ввода исходных чисел удобно использовать строковый тип данных. Задача 4.4 Рассмотрим следующий вариант решения. Создадим массив R(3), где R1, R2, R3 - количество роботов соответствующего возраста. Тогда общее количество роботов S= R1+ R2+ R3. Обозначим x - количество троек, y - количество пятерок, которое можно сформировать из общего числа роботов (идея разбиения на тройки и пятерки рассмотрена в задаче 1.5). Каждый год роботы стареют, общее количество роботов увеличивается на 5x+9y и уменьшается на R3 (число роботов, проживших 3 года). Программа решения может быть записана так: var k,i,n,p:integer; s,x,y:longint; r:array [1..3] of longint;begin write('Начальное количество роботов k='); readln(k); write('Число лет n='); readln(n); r[1]:=k; r[2]:=0; r[3]:=0; s:=k; for i:=1 to n do begin x:=s div 3; p:=s mod 3; if p=0 then y:=0 else if p=1 then begin x:=x-3; y:=2 end else begin x:=x-1; y:=1 end; r[3]:=r[2]; r[2]:=r[1]; r[1]:=5*x+9*y; s:=r[1]+r[2]+r[3]; end; writeln('s=',s)end.В этой программе использовался тип longint, предназначенный для хранения больших целых чисел (до 2147483647). Это связано с тем, что общее число роботов увеличивается очень быстро. Так, например, если начальное число роботов - 10, то через 10 лет их будет 143702. Задача 4.5 Представим лист бумаги в виде числовой матрицы А(8x8). Обозначим заштрихованные клетки единицами, а чистые - нулями. Эта функция будет возвращать значение "истина" (true), если заштрихованных клеток в рассматриваемом прямоугольнике нет, и "ложно" (false) - в противном случае. Здесь maxs - площадь полученного прямоугольника, (maxi1, maxj1) - координаты его левой верхней вершины, (maxi2, maxj2) - координаты его правой нижней вершины. Задача 4.6 Подобные задачи достаточно просто реализуются с использованием рекурсии. Решение построим следующим образом: представим лист в виде числовой матрицы А(nxm). Обозначим заштрихованные клетки единицами, а чистые - нулями. Напишем рекурсивную процедуру, которая определяет площадь заштрихованной фигуры и заменяет клетки уже просмотренной фигуры двойками (чтобы не просматривать эту фигуру ещё раз). В основной программе организуем цикл перебора всех элементов матрицы. Если очередной элемент равен 1 (ещё не просмотренная фигура), то будем вызывать процедуру определения площади этой фигуры). Здесь n и m - число столбцов и строк в рассматриваемой матрице, i, j - координаты найденной клетки фигуры, s - переменная, в которой накапливается площадь фигуры. Процедура учитывает найденную клетку в площади, потом проверяет, заштрихована ли клетка, которая расположена ниже просматриваемой (если это не последняя строка), и если да, то рекурсивно вызывается с этой клетки, потом тот же процесс повторяется для клеток расположенных справа, слева и сверху от рассматриваемой. Рабочая часть основной программы будет иметь вид: max:=0; im:=0; jm:=0;for i:=1 to n dofor j:=1 to m do if a[i,j]=1 then begin s:=0; zaliv(i,j,s); if s>max then begin max:=s; im:=i; jm:=j; end; end;writeln('Smax=',max,' im=',im,' jm=',jm);Здесь max - переменная, в которой хранится максимальная площадь фигуры, im, jm - координаты первой найденной точки этой фигуры. Задача 4.8 Наиболее простым способом решения задач по поиску пути является рекурсивный поиск. Его алгоритм во многом аналогичен рассмотренному в задаче 4.6. Здесь - labir - матрица-константа 4x5, задающая пример лабиринта, f - переменная, через которую отслеживается, есть ли проход из начальной точки в конечную или нет, процедура halt - стандартная процедура, которая прекращает выполнение программы. 1 0 0 8 1 Задача 4.11 Для решения этой задачи рассмотрим стандартную задачу перебора всех возможных сочетаний элементов некоторого массива. Пусть X(n) - массив с элементами 1, 2, … n (массив номеров). Напишем программу, которая на основе этого массива генерирует все подмножества номеров, состоящие из m элементов. Далее рассмотрим функцию, которая на основе очередного сочетания получает следующее по порядку сочетание: function posl(m:integer):boolean;var j,f:integer;label 10,20;begin f:=0; posl:=true; for j:=m downto 1 do if x[j]=n+j-m then f:=j else begin inc(x[j]); goto 10 end;10: if f<>0 then if f=1 then begin posl:=false; goto 20 end else for j:=f to m do x[j]:=x[f-1]+j-f+1;20:end;Эта функция возвращает значение "истина" (true), если переданное сочетание не последнее (для рассмотренного примера: (1,3,4) или (2,4,5)), и значение "ложь" (false), если переданное в функцию сочетание последнее (для рассмотренного примера - (3,4,5)). Функция использует только первые m элементов массива X(n). В первом цикле проверяется, можно ли увеличить какой-либо из элементов массива (начиная с последнего). Если можно увеличить последний (m-й) элемент, то он увеличивается, служебной переменной f присваивается значение 0, и происходит выход из функции (например, из последовательности (1,2,4) получается последовательность (1,2,5)). Если последний элемент уже нельзя увеличить (например, последовательность (1,4,5)), то находится элемент, который еще можно увеличить (в данном случае 1), этот элемент увеличивается, а во втором цикле вслед за ним выстраиваются остальные (таким образом, из (1,4,5) получим (2,3,4)). В этом случае в f сохраняется номер элемента, следующего за увеличенным. Удобство написанной функции в том, что, для получения всех возможных сочетаний из n номеров достаточно добавить в основную часть программы цикл по m: begin for m:=n downto 1 do begin for j:=1 to m do x[j]:=j; repeat printm(m); until not posl(m); end;end.Для решения основной задачи необходимо удалить из обеих строк пробелы, далее перебирать в порядке убывания длины сочетания из букв одной строки и проверять, входят ли они в другую (если да, то решение найдено). Программа, решающая задачу, будет иметь вид: const k=255;var x: array [1..k] of integer; m,n,j: integer; s1,s2,s: string;label 1;…{Описание процедуры posl}…procedure prints(m:integer);var i:integer;begin write(m,': '); for i:=1 to m do write(s1[x[i]]); writeln; readln;end;function spc(s:string):string;var str:string; i:integer;begin str:=''; for i:=1 to length(s) do if s[i]<>' ' then str:=str+s[i]; spc:=str;end;function equal(m:integer):boolean;var i,j:integer;begin j:=1; for i:=1 to length(s2) do if (s1[x[j]]=s2[i])and(j<=m) then j:=j+1; if j>m then equal:=true else equal:=false;end;begin writeln('Введите первую строку'); readln(s1); writeln('Введите вторую строку'); readln(s2); s1:=spc(s1); s2:=spc(s2); if (length(s2)<length(s1)) then begin s:=s1; s1:=s2; s2:=s end; n:=length(s1); for m:=n downto 1 do begin for j:=1 to m do x[j]:=j; repeat if equal(m) then begin prints(m); goto 1; end; until not posl(m); end;1:end.В этой программе процедура prints печатает найденную последовательность символов и её длину, функция equal проверяет, входит ли очередная последовательность, составленная из символов одной строки в другую, функция spc удаляет из переданной в неё строки пробелы. Задача 4.13 Эта задача решена во многих книгах по программированию (например, в [4,5]). Так как ферзей 8, то очевидно, что на каждой вертикали и горизонтали будет стоять по одному ферзю, поэтому можно считать, что ферзь с номером k стоит на k-той вертикали и необходимо найти его координату по горизонтали. Задача 4.14 Как и в предыдущей задаче, будем считать, что на каждой вертикали стоит по ладье, и для каждой из них необходимо найти координату по горизонтали (причем не совпадающую с соответствующими координатами остальных ладей). Таким образом, исходная задача сводится к нахождению всех возможных перестановок из 4 элементов. Известно, что число перестановок из n элементов равно n!=1*2*3*…*n. Например, из 3 элементов можно получить 3!= 1*2*3=6 перестановок: Эта программа работает по следующему принципу: первоначально процедура perest будет рекурсивно вызываться до тех пор, пока не будет распечатан исходный массив X (без перестановки элементов): Массив X(n) в этой программе - массив номеров, массив C(n) - служебный массив, который используется для отслеживания числа сделанных перестановок.
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 662; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.37.177 (0.017 с.) |

 получим dcba efghi.
получим dcba efghi.  получим dcba ihgfe.
получим dcba ihgfe.  получим efghi abcd (что и требовалось получить).
получим efghi abcd (что и требовалось получить). 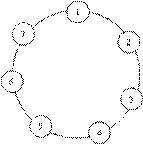 В круге стоят N человек (рис.). Они пронумерованы от 1 до N. Поочередно из круга начинает выходить каждый третий человек. Это продолжается до тех пор, пока в круге не останется последний человек. Определить его номер.
В круге стоят N человек (рис.). Они пронумерованы от 1 до N. Поочередно из круга начинает выходить каждый третий человек. Это продолжается до тех пор, пока в круге не останется последний человек. Определить его номер.  Для приведенного примера координаты вершин (3,4) и (7,6), площадь 15 клеток.
Для приведенного примера координаты вершин (3,4) и (7,6), площадь 15 клеток.

 10500.
10500. 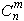 (см. задачу 2.3), то есть
(см. задачу 2.3), то есть  .
. 


