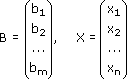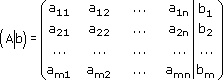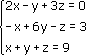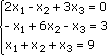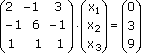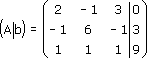Кафедра информатики, информационных технологий и систем управления

КУРСОВАЯ РАБОТА

по дисциплине «Информатика»

«Автоматизация инженерных задач»

 

Выполнил: студент 14 группы инж.фак.

Панов Р.А.

Проверил: Залесов П.В.

Великие Луки - 2012

Введение

1. Описание численных методов решения СЛАУ

1.1. Матричный метод

1.2. Метод простой итерации

2. Прикладное ПО, применяемое для решения СЛАУ

3. Автоматизация решения СЛАУ

3.1. Постановка задачи

3.2. Вычисление СЛАУ матричным методом

3.2.1. Традиционный способ решения СЛАУ

3.2.2. Решение СЛАУ с помощью MS Excel

3.3. Вычисления СЛАУ методом простой итерации.

3.3.1. Традиционный способ решения СЛАУ

3.3.2. Решение СЛАУ с помощью MS Excel

Заключение

Список литературы

 

 

Введение

Многие инженерные задачи требуют решения системы линейных алгебраических уравнений (СЛАУ). С появлением ВТ в математике активно развивается направление, связанное с реализацией методов решения таких задач с помощью ЭВМ, которое называют вычислительной математикой. Для решения инженерных задач на ЭВМ с использованием численных методов чаще всего применяются готовые программы обеспечения, например, MathCAD, MS Excel и другие.

Линейные системы имеют в вычислениях очень большое зна­чение, так как к ним сводится приближенное решение широкого круга вычислительных задач вообще и инженерных задач в ча­стности. Теория решения линейных систем достаточно хорошо разработана и во многих частях доведена до совершенства. Име­ется большое число разнообразных программных средств для ре­шения самых различных систем уравнений, в том числе плохо обусловленных, блочных, с разреженными матрицами и т.д.

Целью курсовой работы являются приобретение навыков автоматизации инженерных расчетов в табличном процессоре MS Excel.

Задачами курсовой работы являются:

1. Решить систему алгебраического уравнения итерационным и матричным методами.

2. Использовать MS Excel в решении системы.

 

 

Описание численных методов решения СЛАУ

Матричный метод

Пусть дана система линейных уравнений:

Рассмотрим матрицу, составленную из коэффициентов при неизвестных:

Свободные члены и неизвестные можно записать в виде матрицы столбцов:

Тогда, используя правило умножение матриц, эту систему уравнений можно записать так:

или

A·x = b. (1)

Равенство (1) называется матричным уравнением или системой уравнений в матричном виде.

Матрица А коэффициентов при неизвестных называется главной матрицей системы.

Иногда рассматривают также расширенную матрицу системы, т. е. главную матрицу системы, дополненную столбцом свободных членов, которую записывают в следующем виде:

Любую линейную систему уравнений можно записать в матричном виде. Например, пусть дана система:

Эта система из двух уравнений с тремя неизвестными – x, y,. В высшей математике можно рассматривать системы из очень большого числа уравнений с большим количеством неизвестных и поэтому неизвестные принято обозначать только буквой х, но с индексами:

Запишем эту систему в матричном виде:

Здесь главная матрица системы:

Расширенная матрица будет иметь вид:

Решения матричных уравнений.

Матричные уравнения решаются при помощи обратных матриц. Уравнение решается следующим образом. Пусть матрица А – невырожденная (D ≠ 0), тогда существует обратная матрица А-1. Умножив на нее обе части матричного уравнения, имеем А-1(АХ) = А-1В. Используя сочетательный закон умножения, перепишем это равенство в виде

(А-1А) Х = А-1В.

Поскольку А-1 А = Е и ЕХ = Х, находим:

Х = А-1В.

Таким образом, чтобы решить матричное уравнение, нужно:

1. Найти обратную матрицу А-1.

2. Найти произведение обратной матрицы А-1 на матрицу столбец свободных членов В, т. е А-1В.

Пользуясь определением равных матриц, записать ответ.

При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений.

К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над расширенной матрицей системы. А в методе Крамера – с определителями системы, образованными по специальному правилу.

Метод простой итерации

 

Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы, подобно тому, как это делается для одного уравнения.

Для определенности ограничимся системой из четырех уравнений с четырьмя неизвестными (система четвертого порядка), которую запишем в виде:

 

Разрешим первое уравнение системы относительно х₁:

х₁ = (-a₁₂/a₁₁)х₂-a₁₃/a₁₁х₃-a₁₄/a₁₁х₄-a₁₅/a₁₁.

Затем разрешим второе уравнение относительно х₂ и т. д. Тогда систему можно переписать в виде:

где α = -a_ik/a_ii, i = 1, 2, 3, 4; k = 1, 2, 3, 4, 5.

Система является частным случаем записи вида:

При этом линейная функция L₁ фактически не зависит от х₁.

Зададим какие-либо начальные значения неизвестных (нулевые приближения):

х₁⁽⁰⁾, х₂⁽⁰⁾, х₃⁽⁰⁾, х₄⁽⁰⁾.

Подставляя эти значения в правые части системы (*), получим первые приближения:

Полученные первые приближения могут быть так же использованы для получения вторых, третьих и т. д. приближений. Т. е. можно записать:

Условия сходимости итерационного процесса.

 

Установим условия, выполнение которых обеспечит сходимость получающихся приближений к истинному (точному) решению системы х₁, х₂, х₃, х₄.

Не вдаваясь в подробности, скажем, что для того чтобы итерационный процесс сходился к точному решению, достаточно, чтобы все коэффициенты системы были малы по сравнению с диагональными.

Это условие можно сформулировать и более точно:

Для сходимости процесса итераций достаточно, чтобы в каждом столбце сумма отношений коэффициентов системы к диагональным элементам, взятым из той же строки, была строго меньше единицы: