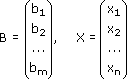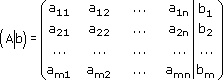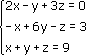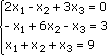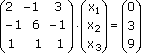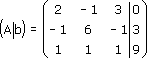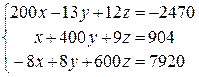Фгбоу впо «великолукская гсха»

Министерство сельского хозяйства РФ

ФГБОУ ВПО «Великолукская ГСХА»

Кафедра информатики, информационных технологий и систем управления

КУРСОВАЯ РАБОТА

по дисциплине «Информатика»

«Автоматизация инженерных задач»

 

Выполнил: студент 14 группы инж.фак.

Панов Р.А.

Проверил: Залесов П.В.

Великие Луки - 2012

Введение

1. Описание численных методов решения СЛАУ

1.1. Матричный метод

1.2. Метод простой итерации

2. Прикладное ПО, применяемое для решения СЛАУ

3. Автоматизация решения СЛАУ

3.1. Постановка задачи

3.2. Вычисление СЛАУ матричным методом

3.2.1. Традиционный способ решения СЛАУ

3.2.2. Решение СЛАУ с помощью MS Excel

3.3. Вычисления СЛАУ методом простой итерации.

3.3.1. Традиционный способ решения СЛАУ

3.3.2. Решение СЛАУ с помощью MS Excel

Заключение

Список литературы

 

 

Введение

Многие инженерные задачи требуют решения системы линейных алгебраических уравнений (СЛАУ). С появлением ВТ в математике активно развивается направление, связанное с реализацией методов решения таких задач с помощью ЭВМ, которое называют вычислительной математикой. Для решения инженерных задач на ЭВМ с использованием численных методов чаще всего применяются готовые программы обеспечения, например, MathCAD, MS Excel и другие.

Линейные системы имеют в вычислениях очень большое зна­чение, так как к ним сводится приближенное решение широкого круга вычислительных задач вообще и инженерных задач в ча­стности. Теория решения линейных систем достаточно хорошо разработана и во многих частях доведена до совершенства. Име­ется большое число разнообразных программных средств для ре­шения самых различных систем уравнений, в том числе плохо обусловленных, блочных, с разреженными матрицами и т.д.

Целью курсовой работы являются приобретение навыков автоматизации инженерных расчетов в табличном процессоре MS Excel.

Задачами курсовой работы являются:

1. Решить систему алгебраического уравнения итерационным и матричным методами.

2. Использовать MS Excel в решении системы.

 

 

Описание численных методов решения СЛАУ

Матричный метод

Пусть дана система линейных уравнений:

Рассмотрим матрицу, составленную из коэффициентов при неизвестных:

Свободные члены и неизвестные можно записать в виде матрицы столбцов:

Тогда, используя правило умножение матриц, эту систему уравнений можно записать так:

или

A·x = b. (1)

Равенство (1) называется матричным уравнением или системой уравнений в матричном виде.

Матрица А коэффициентов при неизвестных называется главной матрицей системы.

Иногда рассматривают также расширенную матрицу системы, т. е. главную матрицу системы, дополненную столбцом свободных членов, которую записывают в следующем виде:

Любую линейную систему уравнений можно записать в матричном виде. Например, пусть дана система:

Эта система из двух уравнений с тремя неизвестными – x, y,. В высшей математике можно рассматривать системы из очень большого числа уравнений с большим количеством неизвестных и поэтому неизвестные принято обозначать только буквой х, но с индексами:

Запишем эту систему в матричном виде:

Здесь главная матрица системы:

Расширенная матрица будет иметь вид:

Решения матричных уравнений.

Матричные уравнения решаются при помощи обратных матриц. Уравнение решается следующим образом. Пусть матрица А – невырожденная (D ≠ 0), тогда существует обратная матрица А-1. Умножив на нее обе части матричного уравнения, имеем А-1(АХ) = А-1В. Используя сочетательный закон умножения, перепишем это равенство в виде

(А-1А) Х = А-1В.

Поскольку А-1 А = Е и ЕХ = Х, находим:

Х = А-1В.

Таким образом, чтобы решить матричное уравнение, нужно:

1. Найти обратную матрицу А-1.

2. Найти произведение обратной матрицы А-1 на матрицу столбец свободных членов В, т. е А-1В.

Пользуясь определением равных матриц, записать ответ.

При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений.

К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над расширенной матрицей системы. А в методе Крамера – с определителями системы, образованными по специальному правилу.

Метод простой итерации

 

Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы, подобно тому, как это делается для одного уравнения.

Для определенности ограничимся системой из четырех уравнений с четырьмя неизвестными (система четвертого порядка), которую запишем в виде:

 

Разрешим первое уравнение системы относительно х₁:

х₁ = (-a₁₂/a₁₁)х₂-a₁₃/a₁₁х₃-a₁₄/a₁₁х₄-a₁₅/a₁₁.

Затем разрешим второе уравнение относительно х₂ и т. д. Тогда систему можно переписать в виде:

где α = -a_ik/a_ii, i = 1, 2, 3, 4; k = 1, 2, 3, 4, 5.

Система является частным случаем записи вида:

При этом линейная функция L₁ фактически не зависит от х₁.

Зададим какие-либо начальные значения неизвестных (нулевые приближения):

х₁⁽⁰⁾, х₂⁽⁰⁾, х₃⁽⁰⁾, х₄⁽⁰⁾.

Подставляя эти значения в правые части системы (*), получим первые приближения:

Полученные первые приближения могут быть так же использованы для получения вторых, третьих и т. д. приближений. Т. е. можно записать:

Условия сходимости итерационного процесса.

 

Установим условия, выполнение которых обеспечит сходимость получающихся приближений к истинному (точному) решению системы х₁, х₂, х₃, х₄.

Не вдаваясь в подробности, скажем, что для того чтобы итерационный процесс сходился к точному решению, достаточно, чтобы все коэффициенты системы были малы по сравнению с диагональными.

Это условие можно сформулировать и более точно:

Для сходимости процесса итераций достаточно, чтобы в каждом столбце сумма отношений коэффициентов системы к диагональным элементам, взятым из той же строки, была строго меньше единицы:

 

 

ЗАПУСК ПРОГРАММЫ EXCEL

Запустить программу для создания, просмотра и работы в электронной таблице можно несколькими способами. Стандартным запуском можно считать следующие действия:

1. Щелкните на кнопке Пуск в левом нижнем углу панели задач.

2. Раскройте меню Программы.

3. В раскрывшемся меню выберите пункт Microsoft Excel.

 

Если пользователь часто обращается к Microsoft Excel, то он, обычно, выносит его в виде ярлыка на Рабочий стол. Тогда запуск, электронной таблицы на выполнение, сводится только к установке курсора на этот ярлык, щелкнув на нем левой клавишей мышки.

 

 

РАБОТА С ФОРМУЛАМИ

 

ОБЩИЕ ПОЛОЖЕНИЯ

 

Числовая обработка внесенных данных в электронную таблицу (ЭТ)¾ одна из главных задач Excel. ЭТ позволяет находить сумму рада чисел, производить вычитание, нахождение процента от общей суммы, строить различного вида графики и т.д.. Однако Excel позволяет производить вычисления по 320-ти функциям. Так, например, по названию товара, из прейскуранта, автоматически возвращается его стоимость и пересылается в указанную ячейку.

При создании, прежде всего, своих формул необходимо помнить ряд правил:

¨ Формулы начинаются со знака равенства (=).

¨ В формулу может входить до 1024-х символов (вряд ли Вам, когда либо, придется руководствоваться этим правилом, но надо помнить о нем!).

¨ Результат вычисления отображается в указанной ячейке, а формула, по которой производилось вычисление, в строке формул.

Как Вы уже успели заметить, необходимо при составлении формул знать фактически не три, а два правила. При необходимости внесения в формулу ссылки на некоторую ячейку легче и, главное, надежнее вводить ее имя не с клавиатуры (возможны ошибки!), а установить курсор мышки на необходимую ячейку и нажать левую клавишу мышки ¾ имя ячейки автоматически введется в формулу.

 

КОПИРОВАНИЕ ФОРМУЛ

 

Вы, наверное, при составлении формул уже убедились в том, что их составление достаточно трудоемкий процесс, даже при использовании мышки, при добавлении в нее ссылок на ячейки. А если таких формул, в процессе вычислений, потребуется несколько? Затраты времени, на их создание, будут возрастать пропорционально их числу. Где же выход? Копирование ¾ вот эффективный выход из создавшегося положения.

Для копирования формулы методом Автозаполнения можно использовать маркер заполнения (этот метод был описан в первой главе). При этом автоматически осуществляется последовательность создания, под вычисляемые строки (столбцы), формул. При копировании формул необходимо учитывать понятия относительных и абсолютных адресов ячеек. При необходимости копирования формулы в другую ячейку или группу ячеек (в этом случае Автозаполнение не годится), можно воспользоваться буфером обмена.

Относительные адреса ячеек появляются при копировании формул с автоматическим преобразованием ссылок на вычисление столбцов или строк таблицы. Так, например, в ячейке F7 записывается сумма строки «Покупка» (ячейки – В7 и С7), а при копировании этой формулы в ячейку F9, строка «Продажа», автоматически вычисляется сумма ячеек В9 и С9 с последующей записью результата в ячейку F9. То есть, имена ячеек В7 и С7, в написанной ранее формуле, автоматически заменились на В9 и С9

Но, иногда, необходимо зафиксировать один из адресов ячейки, тогда запись исходной формулы принимает вид, например:

=СУММ(А1:А4)*$А$5

Здесь, $А$5 – фиксированное имя ячейки, так, при переходе на колонку с именем В, формула автоматически преобразуется в:

=СУММ(В1:В4)*$А$5

При такой записи имени ячейки, с использованием знака «доллар» ($), называется ¾ абсолютным адресом ячейки.

 

Функция – это уже готовая сложная формула, по которой проводятся операции вычисления над группой данных определенного типа. Функции задаются с помощью формул, которые выполняют вычисления по заданным величинам, называемым аргументами, и в указанном порядке, называемом синтаксисом. Например, функция СУММ складывает значения или группы ячеек, а функция ППЛАТ вычисляет величину выплаты за один период годовой ренты на основе постоянных выплат и постоянной процентной ставки. Функцию можно вводить в ячейку самостоятельно или при помощи Мастера функций.

• Мастер функций позволяет использовать весь набор функций Excel, даже если вы точно не знаете их названия. Все функции организованы в группы (или категории), такие как Financial (Финансовые), Statistical (Статистические) и др. Мастер функций выводит краткое описание каждой функции, благодаря которому вы сможете выбрать нужную функцию. Кроме того, мастер функций помогает вводить аргументы функции и поясняет, для чего они нужны. При использовании мастера функций практически исключаются ошибки при записи формул в ячейки, кроме того, так удобнее вводить сложные функции с несколькими аргументами.

Для того, чтобы воспользоваться мастером функций необходимо:

1. Выделите ячейку, в которую нужно поместить функцию, и нажмите кнопку Вставка функции на стандартной панели инструментов.

2. В списке Категории функций открывшегося окна диалога укажите нужную категорию функции.

3. Выберите нужную вам функцию в списке Имя функции. В нижней части окна диалога появится описание выбранной функции. Прочитайте его и убедитесь, что функция выбрана правильно. Щелкните на кнопке ОК.

4. Под строкой формул появится окно — так называемая палитра формул. Введите аргументы в соответствующие поля. Вы можете вводить значения или адреса ячеек вручную, а можете щелкать на нужных ячейках или выделять нужные диапазоны.

5. Щелкните на кнопке ОК, чтобы завершить ввод функции. Результат вычисления функции появится в ячейке.

ФАКТР(число)

Число - это неотрицательное число, факториал которого вычисляется. Если число не целое, то производится отбрасывание дробной части.

МОПРЕД - возвращает определитель матрицы (матрица хранится в массиве).

МОПРЕД(массив)

Массив - это числовой массив с равным количеством строк и столбцов.

Массив может быть задан как интервал ячеек, например, A1:C3 или как массив констант, например {1;2;3:4;5;6:7;8;9}.

КОРЕНЬ - возвращает положительное значение квадратного корня.

КОРЕНЬ(число)

Число - это число, для которого вычисляется квадратный корень. Если число отрицательно, то функция КОРЕНЬ возвращает значение ошибки #ЧИСЛО!.

ABS - возвращает модуль (абсолютную величину) числа. Абсолютная величина числа - это число без знака.

ABS(число)

Число - это действительное число, абсолютную величину которого требуется найти.

ПИ - возвращает число 3,14159265358979, математическую константу p с точностью до 15 цифр

Автоматизация решения СЛАУ

Постановка задачи

Решить систему линейных алгебраических уравнений 2-мя способами: матричным методом и методом простой итерации с точностью e=0,01

 

 

Я итерация

 

Требуемая точность не достигнута

 

Я итерация

Требуемая точность достигнута

Таким образом,

 

 

Заключение

Ещё совсем недавно основными инструментами инженера были калькулятор и чертёжная доска. Расчёты занимали немало рабочего времени. Например, большинство инженерных расчётов проводятся в нескольких приближениях, т.е. один и тот же алгоритм вычислений повторяется несколько раз, но каждый раз с новыми, уточнёнными данными. Инженер вынужден был повторять на калькуляторе вычислительные операции каждого приближения снова и снова. Выполнение чертежей также было нелегким занятием. За кульманом (большая чертёжная доска с закреплённой на ней рейсшиной) как правило, работали стоя, что приводило к возникновению профессиональных болезней. Так как чертежи выполнялись при помощи карандашей различной твёрдости или туши, то неосторожное движение рукой приводило к появлению на чертежах грязных разводов и смазанных линий. В современных условиях рыночной экономики, такой подход, несомненно, не позволит предприятию быть конкурентоспособным и получать прибыль. При размещении заказа на выполнение проектных работ одним из основных критериев является минимальное время выполнения проекта. Автоматизация инженерной работы (расчётов, выполнения чертежей и текстовых документов) позволяет сократить время выполнения проекта в несколько раз. Для этого требуется оборудовать место работы инженера персональным компьютером и установить на него соответствующее программное обеспечение.

 

 

 

СПИСОК ЛИТЕРАТУРЫ

 

 

1. А.В. Голышева, В.Н. Корнеев. Excel 2007 "без воды". Все, что нужно для уверенной работы. -СПб.: Наука и Техника, 2008. -192 с.: ил.

2. Ю. В. Васильков, Н. М. Василькова. Компьютерные технологии вычислений: Учеб. Пособие. – М.: Финансы и статистика, 2007. – 256с.: ил.

3. В. В. Трофимова. Информатика. Издательства «Юрайт», «ИД Юрайт», 2011. – 911с.: ил.

4. Н. А. Лизунова, С. П. Шкроба. Матрицы и системы линейных уравнений. 2007. – 352с.: ил.

5. Е. А. Веденеева. Функции и формулы Excel 2007. Библиотека пользователя. – СПб.: Питер, 2008. – 384с.: ил. – (Серия «Библиотека пользователя»).

6. А. Г. Днепров. Видеосамоучитель Excel 2007 (+ CD) - СПб. [и др.]: Питер, 2007. - 202 с.; 24 см. + 1 электрон. опт. диск. - (Очевидное обучение) (Видеосамоучитель).

7. И. Киреев, А. В. Пантелеев. Численные методы в примерах и задачах.: Учеб. Пособие – 3-е изд. стер. – М.: Высш. шк., 2008. – 480с.: ил.

8. Симонович С.В. и др. Информатика Базовый курс: Учеб, для технических вузов. СПБ: Изд. «Питер», 2007.–640с

9. Могилев А.В., Пак Н.И., Хеннер Е.К. "Практикум по информатике" - М.: Изд. центр "Академия", 2009.

10. Могилев А.В., Пак Н.И., Хеннер Е.К. "Информатика. Учебное пособие" - М.: Изд. центр "Академия", 2008.

11. Могилев А.В., Пак Н.И., Хеннер Е.К. "Информатика. Учебное пособие для студентов педагогических вузов" - М.: Изд. центр "Академия", 2008.

12. Могилев А.В., Хеннер Е.К., Пак Н.И. Информатика. М.: Изд. центр "Академия", 2008

13. Степанов А.Н. Информатика для студентов гуманитарных специальностей. - СПб.: Питер, 2009

14. Турецкий В.Я. Математика и информатика М.: Инфра-М, 2008

15. Жолков С.Ю. Математика и информатика для гуманитариев: Учеб. для вузов. - М.: Гардарики, 2009.

 

Министерство сельского хозяйства РФ

ФГБОУ ВПО «Великолукская ГСХА»