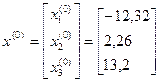Решение СЛАУ с помощью MS Excel

 

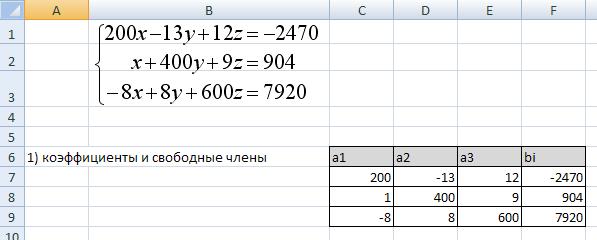
1. Переименуйте Лист1 в Матричный метод.

Запишите коэффициенты при неизвестных (а1, а2, а3) и свободные члены b_i, т.е. сформируйте матрицу систему.

 

 

 

2. Найдите обратную матрицу с помощью функции МОБР().

а) Поместите курсор в ячейку С12:E14.

б) Перейдите на вкладку Формулы. В группе Библиотека функций из списка Математические выберите функцию МОБР().

МОБР (массив) - возвращает обратную матрицу для матрицы, хранящейся в массиве.

Массив — обязательный аргумент. Числовой массив с равным количеством строк и столбцов.

в) В окне Аргументы функции в поле Массив введите диапазон ячеек, содержащий коэффициенты – С7:E9.

г) Нажмите комбинацию клавиш Ctrl+Shift+Enter.

д) Результат выполненных операций

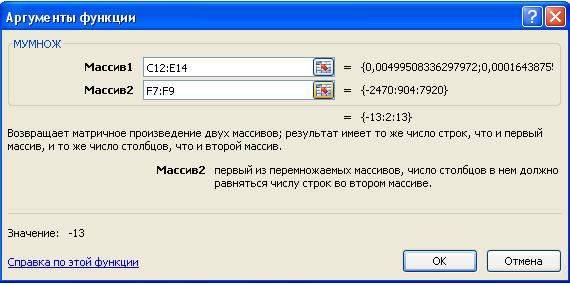
3. Для нахождения неизвестных необходимо умножить обратную матрицу на вектор свободных членов b_i. Умножение матриц можно выполнить с помощью функции МУМНОЖ().

а) Выделите диапазон ячеек С17:С19.

б) Перейдите на вкладку Формулы. В группе Библиотека функций из списка Математические выберите функцию МУМНОЖ().

в) В окне Аргументы функции в поле Массив1 введите диапазон ячеек, содержащий коэффициенты – С12:E14, в поле Массив2 – вектор свободных членов b_i – F7:F9.

г) Нажмите комбинацию клавиш Ctrl+Shift+Enter.

д) Результат выполненных операций

 

 

Вычисления СЛАУ методом простой итерации.

Традиционный способ решения СЛАУ

1. Проверьте условие сходимости

2. Приведите систему к нормальному виду, т.е. из первого уравнения выразите x₁, из второго x₂, из третьего x₃.

 

3. Разделите первое уравнение на 200, второе на 400, третье на 600.

 

4. Выберите начальное приближение

 

5. Итерационный процесс

Я итерация

 

Требуемая точность не достигнута

 

Я итерация

Требуемая точность достигнута

Таким образом,

 

 

Решение СЛАУ с помощью MS Excel

 

1. Переименуйте Лист2 в метод простых итераций.

2. Запишите коэффициенты при неизвестных (а1, а2, а3) и свободные члены b_i, т.е. сформируйте матрицу систему.

3. В ячейки G2:G4 введите точное решение уравнений, используя ссылки на ячейки С17:С19 листа Матричный метод.

4. В ячейку E1 введите точность e, равной 0,01.

 

Результаты выполненных действий

 

 

5. Проверьте условие сходимости с помощью функции ЕСЛИ

Результат вычислений

6.. Введите в ячейки C19:E19 формулы, вычисляющие начальные приближения

к точному значению x1, x2 x3, в ячейки C20:E20 – итерационные формулы, вычисляющие последовательные приближения к точному значению x1, x2, x3.

 

Результат вычислений

 

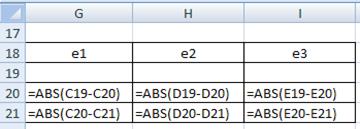
7. В ячейки G20:I20 введите формулы, вычислите критерии

окончания итерационного процесса для x1, x2 и x3.

 

8. В ячейку K20 введите условие окончания итерационного процесса с

помощью функции ЕСЛИ.

Результаты вычислений

9. Копируйте формулы итерационного процесса, критериев и условия

окончания итерационного процесса до тех пор, пока критерии e1, e2 и e3 не достигнут значения, меньше заданного (e=0,01).

Результаты вычислений

 

 

Заключение

Ещё совсем недавно основными инструментами инженера были калькулятор и чертёжная доска. Расчёты занимали немало рабочего времени. Например, большинство инженерных расчётов проводятся в нескольких приближениях, т.е. один и тот же алгоритм вычислений повторяется несколько раз, но каждый раз с новыми, уточнёнными данными. Инженер вынужден был повторять на калькуляторе вычислительные операции каждого приближения снова и снова. Выполнение чертежей также было нелегким занятием. За кульманом (большая чертёжная доска с закреплённой на ней рейсшиной) как правило, работали стоя, что приводило к возникновению профессиональных болезней. Так как чертежи выполнялись при помощи карандашей различной твёрдости или туши, то неосторожное движение рукой приводило к появлению на чертежах грязных разводов и смазанных линий. В современных условиях рыночной экономики, такой подход, несомненно, не позволит предприятию быть конкурентоспособным и получать прибыль. При размещении заказа на выполнение проектных работ одним из основных критериев является минимальное время выполнения проекта. Автоматизация инженерной работы (расчётов, выполнения чертежей и текстовых документов) позволяет сократить время выполнения проекта в несколько раз. Для этого требуется оборудовать место работы инженера персональным компьютером и установить на него соответствующее программное обеспечение.

 

 

 

СПИСОК ЛИТЕРАТУРЫ

 

 

1. А.В. Голышева, В.Н. Корнеев. Excel 2007 "без воды". Все, что нужно для уверенной работы. -СПб.: Наука и Техника, 2008. -192 с.: ил.

2. Ю. В. Васильков, Н. М. Василькова. Компьютерные технологии вычислений: Учеб. Пособие. – М.: Финансы и статистика, 2007. – 256с.: ил.

3. В. В. Трофимова. Информатика. Издательства «Юрайт», «ИД Юрайт», 2011. – 911с.: ил.

4. Н. А. Лизунова, С. П. Шкроба. Матрицы и системы линейных уравнений. 2007. – 352с.: ил.

5. Е. А. Веденеева. Функции и формулы Excel 2007. Библиотека пользователя. – СПб.: Питер, 2008. – 384с.: ил. – (Серия «Библиотека пользователя»).

6. А. Г. Днепров. Видеосамоучитель Excel 2007 (+ CD) - СПб. [и др.]: Питер, 2007. - 202 с.; 24 см. + 1 электрон. опт. диск. - (Очевидное обучение) (Видеосамоучитель).

7. И. Киреев, А. В. Пантелеев. Численные методы в примерах и задачах.: Учеб. Пособие – 3-е изд. стер. – М.: Высш. шк., 2008. – 480с.: ил.

8. Симонович С.В. и др. Информатика Базовый курс: Учеб, для технических вузов. СПБ: Изд. «Питер», 2007.–640с

9. Могилев А.В., Пак Н.И., Хеннер Е.К. "Практикум по информатике" - М.: Изд. центр "Академия", 2009.

10. Могилев А.В., Пак Н.И., Хеннер Е.К. "Информатика. Учебное пособие" - М.: Изд. центр "Академия", 2008.

11. Могилев А.В., Пак Н.И., Хеннер Е.К. "Информатика. Учебное пособие для студентов педагогических вузов" - М.: Изд. центр "Академия", 2008.

12. Могилев А.В., Хеннер Е.К., Пак Н.И. Информатика. М.: Изд. центр "Академия", 2008

13. Степанов А.Н. Информатика для студентов гуманитарных специальностей. - СПб.: Питер, 2009

14. Турецкий В.Я. Математика и информатика М.: Инфра-М, 2008

15. Жолков С.Ю. Математика и информатика для гуманитариев: Учеб. для вузов. - М.: Гардарики, 2009.