Типичные примитивные объекты

· Линии и ломаные линии.

· Многоугольники.

· Окружности и эллипсы.

· Кривые Безье.

· Безигоны.

· Текст (в компьютерных шрифтах, таких как TrueType, каждая буква создаётся из кривых Безье).

Этот список неполон. Есть разные типы кривых (Catmull-Rom сплайны, NURBS и т. д.), которые используются в различных приложениях.

Также возможно рассматривать растровое изображение как примитивный объект, ведущий себя как прямоугольник.

 

 

Кривая Безье.

Кривая Безье:

В качестве формулы, которая была бы достаточно простой (с точки зрения математика), универсальной (с точки зрения программиста) и геометрически наглядной (с точки зрения пользователя — художника или дизайнера), чаще всего используется упомянутая кривая Безье. На самом деле, это целое семейство кривых, из которых используется частный случай с кубической степенью, т. е. кривая третьего порядка, описываемая следующим параметрическим уравнением:

 

R(t) = Po(l-t)3 + P1t(l-t)2 + P2t2(l-t) + Р3t3, где 0 < t < 1.

 

Такую кривую можно построить, если известны координаты четырех точек, называемых контрольными.

Из четырех контрольных точек кривая проходит только через две, поэтому эти точки называются опорными — anchor points (иначе они называются узлами (nodes), поскольку "связывают" элементарные кривые друг с другом, чтобы образовать единый сложный контур).

Две другие контрольные точки не лежат на кривой, но их расположение определяет кривизну кривой, поэтому эти точки иначе называются управляющими точками, а линии, соединяющие управляющую и опорную точки, управляющей линией (в просторечии именуемых "рычагами").

Кривая Безье является гладкой кривой, т. е. она не имеет разрывов и непрерывно заполняет отрезок между начальной и конечной точками.

Кривая начинается в первой опорной точке, касаясь отрезка своей управляющей линии, и заканчивается в последней опорной точке, также касаясь отрезка своей управляющей линии. Это позволяет гладко соединять две кривые Безье друг с другом: управляющие линии располагаются вдоль одной прямой, которая является касательной к получившейся кривой (рис. 4.2).

Кривая лежит в выпуклой оболочке, создаваемой управляющими линиями (рис. 4.3). Это свидетельствует о стабильности ("благонравном поведении") кривой.

Кривая Безье симметрична, т. е. она сохраняет свою форму, если изменить направление вектора кривой на противоположный ("поменять местами" начальную и конечную опорные точки). Это свойство находит свое применение при создании составных контуров. Смотрите об этом в главе 7.

Кривая Безье, используя математический язык, "аффинно инвариантна", т. е. она сохраняет свою форму при масштабировании (рис. 4.4). Это свойство является фундаментом свободы манипулирования объектами векторной графики.

Если существует только две контрольных точки (опорных точки) или управляющие линии коллинеарны (лежат на одной прямой), кривая превращается в прямой отрезок

Изменение положения хотя бы одной из контрольных точек ведет к изменению формы всей кривой Безье. Это свойство — источник бесконечного разнообразия форм векторных объектов.

Из множества таких элементарных кривых составляется контур произвольной формы и произвольной сложности (ограничения появляются в конкретных приложениях и конкретных технических системах).

 

8. Типы компьютерной графики.

Компьютерную графику можно классифицировать по нескольким критериям:

1) в зависимости от способа формирования изображений:

 растровая

 векторная

 фрактальная.

 

2) в зависимости от координат измерения (в этом типе компьютерной графики могут сочетаться векторный и растровый способы формирования изображений):

 плоская, двухмерная

 объемная, трехмерная (или 3D-графика).

 

3) в зависимости от специализации в отдельных областях (в этом типе компьютерной графики могут сочетаться векторный и растровый способы формирования изображений):

 инженерная графика

 научная графика

 Web-графика

 компьютерная полиграфия и т.д.

Понятие фрактал.

Фрактал - объект, обладающий бесконечной сложностью, позволяющий рассмотреть столько же своих деталей вблизи, как и издалека. Земля - классический пример фрактального объекта. Из космоса она выглядит как шар. Если приближаться к ней, мы обнаружим океаны, континенты, побережья и цепи гор. Будем рассматривать горы ближе - станут, видны еще более мелкие детали: кусочек земли на поверхности горы в своем масштабе столь же сложный и неровный, как сама гора. И даже еще более сильное увеличение покажет крошечные частички грунта, каждая из которых сама является фрактальным объектом.

. Фрактальная графика

Фрактальная графика, как и векторная — вычисляемая, но отличается от нее тем, что никакие объекты в памяти компьютера не хранятся. Изображение строится по уравнению (или по системе уравнений), поэтому ничего, кроме формулы, хранить не надо. Изменив коэффициенты в уравнении, можно получить совершенно другую картину. Простейшим фрактальным объектом является фрактальный треугольник. Постройте обычный равносторонний треугольник со стороной а. Разделите каждую из его сторон на три отрезка. На среднем отрезке стороны постройте равносторонний треугольник со стороной, равной 1/3 стороны исходного треугольника, а на других отрезках постройте равносторонние треугольники со стороной, равной 1/9а. С полученными треугольниками повторите те же операции. Вскоре вы увидите, что треугольники последующих поколений наследуют свойства своих родительских структур. Так рождается фрактальная фигура. Процесс наследования можно продолжать до бесконечности. Взяв такой бесконечный фрактальный объект и рассмотрев его в лупу или микроскоп, можно найти в нем все новые и новые детали, повторяющие свойства исходной структуры.

 

 

9. Сжатие графических данных.

Сжатие без потерь (англ. Lossless data compression) — метод сжатия данных: видео, аудио, графики, документов представленных в цифровом виде, при использовании которого закодированные данные могут быть восстановлены с точностью до бита. При этом оригинальные данные полностью восстанавливаются из сжатого состояния. Этот тип сжатия принципиально отличается от сжатия данных с потерями. Для каждого из типов цифровой информации, как правило, существуют свои оптимальные алгоритмы сжатия без потерь.

Сжатие данных без потерь используется во многих приложениях. Например, оно используется во всех файловых архиваторах. Оно также используется как компонент в сжатии с потерями.

Сжатие без потерь используется, когда важна идентичность сжатых данных оригиналу. Обычный пример — исполняемые файлы и исходный код. Некоторые графические файловые форматы, такие как PNG, используют только сжатие без потерь; тогда как другие (TIFF, MNG) или GIF могут использовать сжатие как с потерями, так и без.

АРХИВАЦИЯ И КОМПРЕССИЯ

Как правило, все методы сжатия графических изображений разделяют на две категории: архивацию и компрессию. Под архивацией понимают сжатие информации с возможностью ее дальнейшего восстановления. Компрессия же означает потерю некоторого количества информации об изображении, что естественно приводит к ухудшению качества, но уменьшает объем сохраненных данных. Архивировать можно как растровую, так и векторную графику. Принцип архивации состоит в том, что программа анализирует наличие в сжимаемых данных одинаковых последовательностей и исключает их, записывая вместо повторяющегося фрагмента ссылку на предыдущий и аналогичный ему для того, чтобы была возможность восстановления. Хорошим примером графического объекта с большим количеством одинаковых последовательностей может стать фотография или рисунок с голубым небом в изображении или со сплошной однотонной заливкой. При таком подходе можно восстанавливать нужную информацию без потерь. Компрессия же не гарантирует полного восстановления исходных данных, поэтому ее основная задача - не "убить" что-нибудь очень ценное в погоне за уменьшением объема. Обычно информация, подвергнутая компрессии, занимает значительно меньше объема, чем сохраненная методами архивации. Именно это обстоятельство и оставляет этому методу место под солнцем. Регулирование степени сжатия дает право на выбор: размер выходного файла или сохранение его качества. Рассмотрим несколько алгоритмов сжатия данных, которые не вносят изменений в исходные файлы и гарантируют полное восстановление данных.

В зависимости от того, в каком объекте размещены данные, подлежащие сжатию различают:

Сжатие (архивация) файлов: используется для уменьшения размеров файлов при подготовке их к передаче каналами связи или к транспортированию на внешних носителях маленькой емкости;

Сжатие (архивация) папок: используется как средство уменьшения объема папок перед долгим хранением, например, при резервном копировании;

Сжатие (уплотнение) дисков: используется для повышения эффективности использования дискового просторную путем сжатия данных при записи их на носителе информации (как правило, средствами операционной системы).

 

 

Закон Ципфа

Закон Ципфа (Зипфа) — эмпирическая закономерность распределения частоты слов естественного языка: если все слова языка (или просто достаточно длинного текста) упорядочить по убыванию частоты их использования, то частота n-го слова в таком списке окажется приблизительно обратно пропорциональной его порядковому номеру n (так называемому рангу этого слова, см. шкала порядка). Например второе по используемости слово встречается примерно в два раза реже, чем первое, третье — в три раза реже, чем первое, и т. д.

Закон носит имя своего первооткрывателя — американского лингвиста Джорджа Ципфа (George Kingsley Zipf) из Гарвардского университета.

 

Простейшие алгоритмы сжатия.

 Преобразование Барроуза — Уилера (также известен как англ. BWT) — предварительная обработка данных для улучшения сжатия без потерь

 Преобразование Шиндлера (англ. ST) — модификация преобразования Барроуза — Уилера

 Алгоритм DEFLATE — популярный свободный алгоритм сжатия (используется в библиотеке zlib)

 Дельта-кодирование — эффективно для сжатия данных, в которых последовательности часто повторяются

 Инкрементное кодирование — дельта-кодирование применяемое к последовательности строк

 Семейство алгоритмов словарного сжатия Лемпеля — Зива:

10. Сжатие графических данных.

Сжатие без потерь (англ. Lossless data compression) — метод сжатия данных: видео, аудио, графики, документов представленных в цифровом виде, при использовании которого закодированные данные могут быть восстановлены с точностью до бита. При этом оригинальные данные полностью восстанавливаются из сжатого состояния. Этот тип сжатия принципиально отличается от сжатия данных с потерями. Для каждого из типов цифровой информации, как правило, существуют свои оптимальные алгоритмы сжатия без потерь.

Сжатие данных без потерь используется во многих приложениях. Например, оно используется во всех файловых архиваторах. Оно также используется как компонент в сжатии с потерями.

Сжатие без потерь используется, когда важна идентичность сжатых данных оригиналу. Обычный пример — исполняемые файлы и исходный код. Некоторые графические файловые форматы, такие как PNG, используют только сжатие без потерь; тогда как другие (TIFF, MNG) или GIF могут использовать сжатие как с потерями, так и без.

АРХИВАЦИЯ И КОМПРЕССИЯ

Как правило, все методы сжатия графических изображений разделяют на две категории: архивацию и компрессию. Под архивацией понимают сжатие информации с возможностью ее дальнейшего восстановления. Компрессия же означает потерю некоторого количества информации об изображении, что естественно приводит к ухудшению качества, но уменьшает объем сохраненных данных. Архивировать можно как растровую, так и векторную графику. Принцип архивации состоит в том, что программа анализирует наличие в сжимаемых данных одинаковых последовательностей и исключает их, записывая вместо повторяющегося фрагмента ссылку на предыдущий и аналогичный ему для того, чтобы была возможность восстановления. Хорошим примером графического объекта с большим количеством одинаковых последовательностей может стать фотография или рисунок с голубым небом в изображении или со сплошной однотонной заливкой. При таком подходе можно восстанавливать нужную информацию без потерь. Компрессия же не гарантирует полного восстановления исходных данных, поэтому ее основная задача - не "убить" что-нибудь очень ценное в погоне за уменьшением объема. Обычно информация, подвергнутая компрессии, занимает значительно меньше объема, чем сохраненная методами архивации. Именно это обстоятельство и оставляет этому методу место под солнцем. Регулирование степени сжатия дает право на выбор: размер выходного файла или сохранение его качества. Рассмотрим несколько алгоритмов сжатия данных, которые не вносят изменений в исходные файлы и гарантируют полное восстановление данных.

В зависимости от того, в каком объекте размещены данные, подлежащие сжатию различают:

1. Сжатие (архивация) файлов: используется для уменьшения размеров файлов при подготовке их к передаче каналами связи или к транспортированию на внешних носителях маленькой емкости;

2. Сжатие (архивация) папок: используется как средство уменьшения объема папок перед долгим хранением, например, при резервном копировании;

3. Сжатие (уплотнение) дисков: используется для повышения эффективности использования дискового просторную путем сжатия данных при записи их на носителе информации (как правило, средствами операционной системы).

 

Алгоритм Хаффмана.

Алгоритм Хаффмана — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.

В отличие от алгоритма Шеннона — Фано, алгоритм Хаффмана остаётся всегда оптимальным и для вторичных алфавитов m₂ с более чем двумя символами.

Кодирование Хаффмана

Один из первых алгоритмов эффективного кодирования информации был предложен Д. А. Хаффманом в 1952 году. Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (т.е. ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.

Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево). ^[1]

1. Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.

2. Выбираются два свободных узла дерева с наименьшими весами.

3. Создается их родитель с весом, равным их суммарному весу.

4. Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.

5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0.

6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.

Допустим, у нас есть следующая таблица частот:

А	Б	В	Г	Д

Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n₀ потомков — символы из предыдущего шага и т. д.

Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от листа дерева, соответствующего этому символу, до корня дерева, накапливая биты при перемещении по ветвям дерева. Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.

Для данной таблицы символов коды Хаффмана будут выглядеть следующим образом.

А	Б	В	Г	Д

Поскольку ни один из полученных кодов не является префиксом другого, они могут быть однозначно декодированы при чтении их из потока. Кроме того, наиболее частый символ сообщения А закодирован наименьшим количеством бит, а наиболее редкий символ Д — наибольшим.

При этом общая длина сообщения, состоящего из приведённых в таблице символов, составит 87 бит (в среднем 2,2308 бита на символ). При использовании равномерного кодирования общая длина сообщения составила бы 117 бит (ровно 3 бита на символ). Заметим, что энтропия источника, независимым образом порождающего символы с указанными частотами составляет ~2,1858 бита на символ, т.е. избыточность построенного для такого источника кода Хаффмана, понимаемая, как отличие среднего числа бит на символ от энтропии, составляет менее 0,05 бит на символ.

Классический алгоритм Хаффмана имеет ряд существенных недостатков. Во-первых, для восстановления содержимого сжатого сообщения декодер должен знать таблицу частот, которой пользовался кодер. Следовательно, длина сжатого сообщения увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию сообщения. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по сообщению: одного для построения модели сообщения (таблицы частот и Н-дерева), другого для собственно кодирования. Во-вторых, избыточность кодирования обращается в ноль лишь в тех случаях, когда вероятности кодируемых символов являются обратными степенями числа 2. В-третьих, для источника с энтропией, не превышающей 1 (например, для двоичного источника), непосредственное применение кода Хаффмана бессмысленно.

Адаптивное сжатие

Адаптивное сжатие позволяет не передавать модель сообщения вместе с ним самим и ограничиться одним проходом по сообщению как при кодировании, так и при декодировании.

В создании алгоритма адаптивного кодирования Хаффмана наибольшие сложности возникают при разработке процедуры обновления модели очередным символом. Теоретически можно было бы просто вставить внутрь этой процедуры полное построение дерева кодирования Хаффмана, однако, такой алгоритм сжатия имел бы неприемлемо низкое быстродействие, так как построение Н-дерева — это слишком большая работа и производить её при обработке каждого символа неразумно. К счастью, существует способ модифицировать уже существующее Н-дерево так, чтобы отобразить обработку нового символа.

Обновление дерева при считывании очередного символа сообщения состоит из двух операций.

Первая — увеличение веса узлов дерева. Вначале увеличиваем вес листа, соответствующего считанному символу, на единицу. Затем увеличиваем вес родителя, чтобы привести его в соответствие с новыми значениями веса потомков. Этот процесс продолжается до тех пор, пока мы не доберемся до корня дерева. Среднее число операций увеличения веса равно среднему количеству битов, необходимых для того, чтобы закодировать символ.

Вторая операция — перестановка узлов дерева — требуется тогда, когда увеличение веса узла приводит к нарушению свойства упорядоченности, то есть тогда, когда увеличенный вес узла стал больше, чем вес следующего по порядку узла. Если и дальше продолжать обрабатывать увеличение веса, двигаясь к корню дерева, то дерево перестанет быть деревом Хаффмана.

Чтобы сохранить упорядоченность дерева кодирования, алгоритм работает следующим образом. Пусть новый увеличенный вес узла равен W+1. Тогда начинаем двигаться по списку в сторону увеличения веса, пока не найдем последний узел с весом W. Переставим текущий и найденный узлы между собой в списке, восстанавливая таким образом порядок в дереве (при этом родители каждого из узлов тоже изменятся). На этом операция перестановки заканчивается.

После перестановки операция увеличения веса узлов продолжается дальше. Следующий узел, вес которого будет увеличен алгоритмом, — это новый родитель узла, увеличение веса которого вызвало перестановку.

Переполнение

В процессе работы алгоритма сжатия вес узлов в дереве кодирования Хаффмана неуклонно растет. Первая проблема возникает тогда, когда вес корня дерева начинает превосходить вместимость ячейки, в которой он хранится. Как правило, это 16-битовое значение и, следовательно, не может быть больше, чем 65535. Вторая проблема, заслуживающая ещё большего внимания, может возникнуть значительно раньше, когда размер самого длинного кода Хаффмана превосходит вместимость ячейки, которая используется для того, чтобы передать его в выходной поток. Декодеру все равно, какой длины код он декодирует, поскольку он движется сверху вниз по дереву кодирования, выбирая из входного потока по одному биту. Кодер же должен начинать от листа дерева и двигаться вверх к корню, собирая биты, которые нужно передать. Обычно это происходит с переменной типа «целое», и, когда длина кода Хаффмана превосходит размер типа «целое» в битах, наступает переполнение.

Можно доказать, что максимальную длину код Хаффмана для сообщений с одним и тем же входным алфавитом будет иметь, если частоты символов образует последовательность Фибоначчи. Сообщение с частотами символов, равными числам Фибоначчи до Fib (18), — это отличный способ протестировать работу программы сжатия по Хаффману.

 

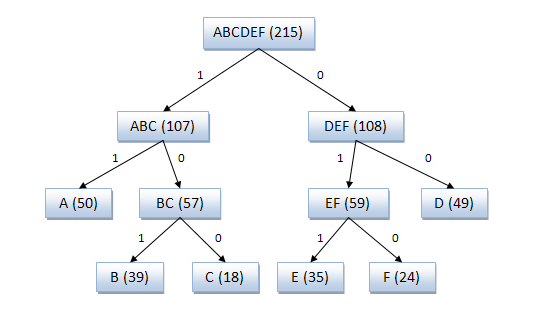
Алгоритм Шеннона-Фано.

Алгоритм Шеннона — Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано (англ. Fano). Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм использует коды переменной длины: часто встречающийся символ кодируется кодом меньшей длины, редко встречающийся — кодом большей длины. Коды Шеннона — Фано префиксные, то есть никакое кодовое слово не является префиксом любого другого. Это свойство позволяет однозначно декодировать любую последовательность кодовых слов.

Кодирование Шеннона — Фано (англ. Shannon-Fano coding) — алгоритм префиксного неоднородного кодирования. Относится к вероятностным методам сжатия (точнее, методам контекстного моделирования нулевого порядка). Подобно алгоритму Хаффмана, алгоритм Шеннона — Фано использует избыточность сообщения, заключённую в неоднородном распределении частот символов его (первичного) алфавита, то есть заменяет коды более частых символов короткими двоичными последовательностями, а коды более редких символов — более длинными двоичными последовательностями.

Алгоритм был независимо друг от друга разработан Шенноном (публикация «Математическая теория связи», 1948 год) и, позже, Фано (опубликовано как технический отчёт).

Основные этапы

1. Символы первичного алфавита m₁ выписывают в порядке убывания вероятностей.

2. Символы полученного алфавита делят на две части, суммарные вероятности символов которых максимально близки друг другу.

3. В префиксном коде для первой части алфавита присваивается двоичная цифра «0», второй части — «1».

4. Полученные части рекурсивно делятся и их частям назначаются соответствующие двоичные цифры в префиксном коде.

Когда размер подалфавита становится равен нулю или единице, то дальнейшего удлинения префиксного кода для соответствующих ему символов первичного алфавита не происходит, таким образом, алгоритм присваивает различным символам префиксные коды разной длины. На шаге деления алфавита существует неоднозначность, так как разность суммарных вероятностей p ₀ − p ₁ может быть одинакова для двух вариантов разделения (учитывая, что все символы первичного алфавита имеют вероятность больше нуля).

[править] Алгоритм вычисления кодов Шеннона — Фано

Код Шеннона — Фано строится с помощью дерева. Построение этого дерева начинается от корня. Всё множество кодируемых элементов соответствует корню дерева (вершине первого уровня). Оно разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Эти подмножества соответствуют двум вершинам второго уровня, которые соединяются с корнем. Далее каждое из этих подмножеств разбивается на два подмножества с примерно одинаковыми суммарными вероятностями. Им соответствуют вершины третьего уровня. Если подмножество содержит единственный элемент, то ему соответствует концевая вершина кодового дерева; такое подмножество разбиению не подлежит. Подобным образом поступаем до тех пор, пока не получим все концевые вершины. Ветви кодового дерева размечаем символами 1 и 0, как в случае кода Хаффмана.

При построении кода Шеннона — Фано разбиение множества элементов может быть произведено, вообще говоря, несколькими способами. Выбор разбиения на уровне n может ухудшить варианты разбиения на следующем уровне (n + 1) и привести к неоптимальности кода в целом. Другими словами, оптимальное поведение на каждом шаге пути ещё не гарантирует оптимальности всей совокупности действий. Поэтому код Шеннона — Фано не является оптимальным в общем смысле, хотя и дает оптимальные результаты при некоторых распределениях вероятностей. Для одного и того же распределения вероятностей можно построить, вообще говоря, несколько кодов Шеннона — Фано, и все они могут дать различные результаты. Если построить все возможные коды Шеннона — Фано для данного распределения вероятностей, то среди них будут находиться и все коды Хаффмана, то есть оптимальные коды.

[править] Пример кодового дерева

Исходные символы:

· A (частота встречаемости 50)

· B (частота встречаемости 39)

· C (частота встречаемости 18)

· D (частота встречаемости 49)

· E (частота встречаемости 35)

· F (частота встречаемости 24)

Кодовое дерево

Полученный код: A — 11, B — 101, C — 100, D — 00, E — 011, F — 010.

Кодирование Шеннона — Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина последовательности, сжатой по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях могут сформироваться неоптимальные коды Шеннона — Фано, поэтому более эффективным считается сжатие методом Хаффмана.

 

11. Сжатие графических данных.

Сжатие без потерь (англ. Lossless data compression) — метод сжатия данных: видео, аудио, графики, документов представленных в цифровом виде, при использовании которого закодированные данные могут быть восстановлены с точностью до бита. При этом оригинальные данные полностью восстанавливаются из сжатого состояния. Этот тип сжатия принципиально отличается от сжатия данных с потерями. Для каждого из типов цифровой информации, как правило, существуют свои оптимальные алгоритмы сжатия без потерь.

Сжатие данных без потерь используется во многих приложениях. Например, оно используется во всех файловых архиваторах. Оно также используется как компонент в сжатии с потерями.

Сжатие без потерь используется, когда важна идентичность сжатых данных оригиналу. Обычный пример — исполняемые файлы и исходный код. Некоторые графические файловые форматы, такие как PNG, используют только сжатие без потерь; тогда как другие (TIFF, MNG) или GIF могут использовать сжатие как с потерями, так и без.

АРХИВАЦИЯ И КОМПРЕССИЯ

Как правило, все методы сжатия графических изображений разделяют на две категории: архивацию и компрессию. Под архивацией понимают сжатие информации с возможностью ее дальнейшего восстановления. Компрессия же означает потерю некоторого количества информации об изображении, что естественно приводит к ухудшению качества, но уменьшает объем сохраненных данных. Архивировать можно как растровую, так и векторную графику. Принцип архивации состоит в том, что программа анализирует наличие в сжимаемых данных одинаковых последовательностей и исключает их, записывая вместо повторяющегося фрагмента ссылку на предыдущий и аналогичный ему для того, чтобы была возможность восстановления. Хорошим примером графического объекта с большим количеством одинаковых последовательностей может стать фотография или рисунок с голубым небом в изображении или со сплошной однотонной заливкой. При таком подходе можно восстанавливать нужную информацию без потерь. Компрессия же не гарантирует полного восстановления исходных данных, поэтому ее основная задача - не "убить" что-нибудь очень ценное в погоне за уменьшением объема. Обычно информация, подвергнутая компрессии, занимает значительно меньше объема, чем сохраненная методами архивации. Именно это обстоятельство и оставляет этому методу место под солнцем. Регулирование степени сжатия дает право на выбор: размер выходного файла или сохранение его качества. Рассмотрим несколько алгоритмов сжатия данных, которые не вносят изменений в исходные файлы и гарантируют полное восстановление данных.

В зависимости от того, в каком объекте размещены данные, подлежащие сжатию различают:

1. Сжатие (архивация) файлов: используется для уменьшения размеров файлов при подготовке их к передаче каналами связи или к транспортированию на внешних носителях маленькой емкости;

2. Сжатие (архивация) папок: используется как средство уменьшения объема папок перед долгим хранением, например, при резервном копировании;

3. Сжатие (уплотнение) дисков: используется для повышения эффективности использования дискового просторную путем сжатия данных при записи их на носителе информации (как правило, средствами операционной системы).

 

Алгоритм RLE.

Алгоритм RLE.
Кодирование длин серий (англ. Run-length encoding, RLE) или Кодирование повторов — простой алгоритм сжатия данных, который оперирует сериями данных, то есть последовательностями, в которых один и тот же символ встречается несколько раз подряд. При кодировании строка одинаковых символов, составляющих серию, заменяется строкой, которая содержит сам повторяющийся символ и количество его повторов.
Очевидно, что такое кодирование эффективно для данных, содержащих большое количество серий, например, для простых графических изображений, таких как иконки и графические рисунки. Однако это кодирование плохо подходит для изображений с плавным переходом тонов, таких как фотографии.

Алгоритм LZW.

Алгоритм LZW.
Алгори́тм Ле́мпеля — Зи́ва — Ве́лча (Lempel-Ziv-Welch, LZW) — это универсальный алгоритм сжатия данных без потерь, созданный Абрахамом Лемпелем (англ. Abraham Lempel), Якобом Зивом (англ. Jacob Ziv) и Терри Велчем (англ. Terry Welch). Он был опубликован Велчем в 1984 году, в качестве улучшенной реализации алгоритма LZ78, опубликованного Лемпелем и Зивом в1978 году. Алгоритм разработан так, чтобы его можно было быстро реализовать, но он не обязательно оптимален, поскольку он не проводит никакого анализа входных данных.

1. Инициализация словаря всеми возможными односимвольными фразами. Инициализация входной фразы w первым символом сообщения.
2. Найти в словаре строку W наибольшей длины, которая совпадает с последними принятыми символами.
3. Считать очередной символ K из кодируемого сообщения.
4. Если КОНЕЦ_СООБЩЕНИЯ, то выдать код для W, иначе
5. Если фраза WK уже есть в словаре, присвоить входной фразе W значение WK и перейти к Шагу 3, иначе выдать код W, добавить WK в словарь, присвоить входной фразе W значение K и перейти к Шагу 3.
6. Конец
На момент своего появления алгоритм LZW давал лучший коэффициент сжатия, для большинства приложений, чем любой другой хорошо известный метод того времени. Он стал первым широко используемым на компьютерах методом сжатия данных.
Алгоритм был реализован в программе compress, которая стала более или менее стандартной утилитой Unix-систем приблизительно в 1986 году. Несколько других популярных утилит-архиваторов также используют этот метод или близкие к нему.
В 1987 году алгоритм стал частью стандарта на формат изображений GIF. Он также может (опционально) использоваться в форматеTIFF.
В настоящее время, алгоритм содержится в стандарте PDF.

 

12. Форматы графических файлов. Растровые форматы.

Форматы графических файлов

GIF - Compuserve Graphics Interchange Format

TIFF - Aldus & Microsoft Tag Image File Format

РСХ - ZSoft РС Paintbrush format

RLE - Compuserve & Teletext Run Length Encoded

ВМР - Microsoft Windows BitMaP

LBM - Deluxe Paint format

PIC - Pictor/PC Paint forma

МАС - MacPaint format

IMG - Gem Paint format

CUT - Dr. Halo Cut files

TGA - Targa format

JPEG - Joint Photographic Experts Group

MEPG - Moving Pictures Experts Group

FLC - AutodeskAnimator

 

растровые (TIFF, GIF, BMP, JPEG);

GIF формат разработан в CompuServe Incorporation для хранения и транспортировки растровых изображений. Поддерживаемая цветовая модель - индексированные цветные изображения. Использует метод кодирования LZW (Lempel, Ziv & Welch), дающий высокий коэффициент сжатия. Позволяет содержать в одном файле несколько изображений, не связанных между собой. Поддерживается многими разработчиками графических систем.

TIFF разработан фирмами Aldus и Microsoft главным образом для настольных издательских систем. Распространенность этого формата обусловлена его гибкостью в части поддерживаемых способов кодирования и цветовых моделей изображения. TIFF поддерживает двух-уровневые (bi-level), монохромные (gray-scale), индексированные цветные (paletted color), и полные цветные (full RGB) изображения. Для кодирования различных изображений или его частей могут применяться различные методы, в частности LZW. Кроме того, TIFF содержит метрические характеристики изображения - размер, плотность и пр. Предусмотрена возможность записи в один файл нескольких изображений и/или копий одного изображения с различными метрическими характеристиками.

BMP (от англ. Bitmap Picture) — формат хранения растровых изображений.

С форматом BMP работает огромное количество программ, так как его поддержка интегрирована в операционные системы Windows и OS/2. Файлы формата BMP могут иметь расширения.bmp,.dib и.rle. Кроме того, данные этого формата включаются в двоичные файлы ресурсов RES и в PE-файлы.

Глубина цвета в данном формате может быть 1, 2, 4, 8, 16, 24, 32, 48 бит на пиксел, максимальные размеры изображения 65535×65535 пикселов. Однако, глубина 2 бит официально не поддерживается.

В формате BMP есть поддержка сжатия по алгоритму RLE, однако теперь существуют форматы с более сильным сжатием, и из-за большого объёма BMP редко используется в Интернете, где для сжатия без потерь используются PNG и более старый GIF.

 

JPEG - стандарт ISO, ориентированный на цифровое описание (сжатие и кодирование) фотоизображений. Он предусматривает возможность частичной потери информации без визуального ухудшения качества изображения.

 

13. Форматы графических файлов. Векторные форматы.

Форматы графических файлов

GIF - Compuserve Graphics Interchange Format

TIFF - Aldus & Microsoft Tag Image File Format

РСХ - ZSoft РС Paintbrush format

RLE - Compuserve & Teletext Run Length Encoded

ВМР - Microsoft Windows BitMaP

LBM - Deluxe Paint format

PIC - Pictor/PC Paint forma

МАС - MacPaint format

IMG - Gem Paint format