Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Радиусы кривизны земного эллипсоидаСодержание книги
Поиск на нашем сайте Плоскости секущие эллипсоид вращения по различным направлениям, образуют в пересечении с его поверхностью или окружности или эллипсы. Основными сечениями эллипсоида являются (рис. 1.5): - сечение плоскостью, проходящей через малую ось; - сечение плоскостью, перпендикулярной малой оси; - нормальное сечение. Сечение плоскостью, проходящей через малую ось РР¢ эллипсоида, образует на его поверхности меридианный эллипс или истинный меридиан «PQP¢Q¢». Кривизна его – переменная величина (радиус кривизны М – тоже). Радиус М уменьшается с уменьшением географической широты (j) и вычисляется по формуле:
где а – большая полуось; е – эксцентриситет Приняв, что
Рис.1.5. Радиусы кривизны земного эллипсоида
Экваториальный радиус кривизны меридиана при j = 0°: М0 = 6 335 552,6 м. Сечение эллипсоида плоскостью перпендикулярной его малой оси РР¢ дает на его поверхности малый круг qq¢ – параллель. Радиус параллели r вычисляется по формуле:
При j = 0° радиус параллели равен большой полуоси а эллипсоида, и эта параллель – земной экватор. Нормальное сечение – сечение эллипсоида плоскостью, проходящей через нормаль к его поверхности. Из бесчисленного множества возможных нормальных сечений выделяют два главных нормальных сечения – меридианное и перпендикулярное ему – сечение первого вертикала. Для сечения первого вертикала радиус кривизны эллипса N, вычисляется по формуле:
на полюсе M = N, M < N; на экваторе N0 = a. Экваториальный радиус кривизны первого вертикала при j = 0°: N0 = a = 6 378 245 м. Радиус кривизны нормального сечения, составляющего с меридианом в заданной точке угол А, вычисляется по формуле:
где М и N – величины, определяемые в зависимости от широты j по формулам (1.4) и (1.7). Радиусом средней кривизны эллипсоида в данной точке с широтой j называют среднее геометрическое из радиуса М и N. Радиус средней кривизны эллипсоида вычисляется по формуле:
Значения М, N, R даны в картографических таблицах УГС через каждые 30¢ j. Произведение любого радиуса кривизны на «arс 1 ¢» равно длине дуги в 1 ¢ данного сечения. Учтя приведенные выше формулы, получим выражение для определения длин дуг: 1) – одной минуты параллели:
или без учета сжатия Земли (е = 0)
2) – одной минуты первого вертикала:
или приближенно:
3) – одной минуты меридиана:
или приближенно:
Таким образом, поверхность земного эллипсоида имеет кривизну, изменяющуюся от точки к точке по широте и от направления в данной точке. Выводы 1. Для решения задач судовождения Земной шар принимается за эллипсоид вращения с элементами референц-эллипсоида Красовского. 2. Положение точки на земной поверхности определяется географическими координатами: - географической широтой (j); - географической долготой (l). 3. Величинами, характеризующими изменение географических координат при переходе судна от одной точки к другой, являются: - разность широт (D j, РШ) и - разность долгот (D l, РД). 4. Форма и размеры земного эллипсоида характеризуются радиусами кривизны его основных сечений (М, r, N, rA, R).
Примечание: Самоконтроль знаний по теме проводится по тестовым заданиям к главе на базе приложения «Компьютерная система тестирования знаний «OPENTEST»». ГЛАВА 2. ОПРЕДЕЛЕНИЕ НАПРАВЛЕНИЙ В МОРЕ Основные линии и плоскости наблюдателя Как нанести по координатам (j, l) точку на карту; как снять с карты координаты (j, l); как рассчитать разность широт (D j) и разность долгот (D l) между пунктами отхода и прихода – все эти вопросы мы уже рассмотрели. Но судно, находясь в море, не стоит на месте а, большей частью, находится в постоянном движении. Для того, чтобы знать направление этого движения, а также направления с судна на различные предметы (навигационные ориентиры, соседние суда и т.д.) нужно выбрать такие линии и плоскости, принимаемые за исходные, от которых можно было бы вести отсчет этих направлений.
Рис. 2.1. Основные линии и плоскости наблюдателя
Построим (рис. 2.1) земной эллипсоид (земную сферу) и предположим, что наблюдатель находится на Гринвичском (начальном) меридиане в верхней части сферы (т. А). Отметим на земной сфере: - т. О – центр сферы; - линия PNPS – ось Земли, а точки PN и PS – северный и южный географические полюсы. Через место наблюдателя (т. А) и центр Земли (т. О) проведем прямую – отвесную линию (ZAOn), тогда: - отвесная линия, проходящая через точку наблюдателя, показывает направления: а) – над головой наблюдателя – на точку Z – зенит наблюдателя; б) – в противоположную сторону – на точку n – надир наблюдателя. Через место наблюдателя (т. А) перпендикулярно отвесной линии (ZAOn) проведем плоскость Н-Н¢, тогда: Ø горизонтальная плоскость, перпендикулярная направлению отвесной линии и проходящая через место (глаз) наблюдателя называется плоскостью истинного горизонта наблюдателя. Надгоризонтная часть – все, что находится над истинным горизонтом и «видимо» для наблюдателя. Подгоризонтная часть – все, что находится под истинным горизонтом и «скрыто» от наблюдателя. Построим плоскость М-М¢, проходящую через место наблюдателя и полюсы Земли (PN и PS), тогда: Ø вертикальная плоскость, проходящая через отвесную линию, место наблюдателя и полюсы Земли, называется плоскостью истинного меридиана наблюдателя. Плоскость истинного меридиана наблюдателя (ИМН) пересекает плоскость истинного горизонта наблюдателя (ИГН) по прямой линии (N-S), называемой линией истинного меридиана наблюдателя (ИМН) или полуденной линией (рис. 2.1 линия NAS). Часть линии ИМН – линия А-N – северная часть ИМН; другая ее часть – линия А-S – южная часть ИМН. Линия ИМН соответствует направлению (от наблюдателя) на северный (PN) и южный (PS) полюсы. На этом основании точка истинного горизонта наблюдателя, определяющая направление на северный полюс (PN), обозначается как N («норд»), а противоположная ей как S («зюйд»). Проведем теперь вертикальную плоскость (О-О¢), которая пройдет через отвесную линию (ZOn) перпендикулярно плоскости ИМН (М-М¢), тогда: вертикальная плоскость, проходящая через отвесную линию и перпендикулярная плоскости ИМН, называется плоскостью I-го вертикала наблюдателя. Плоскость I-го вертикала наблюдателя (О-О¢) пересекает плоскость истинного горизонта наблюдателя (Н-Н¢) по линии, указывающей направление на восток – т. Е («ист») и запад – т. W («вест»). Направления N («норд»), S («зюйд»), Е («ист»), W («вест») называются главными направлениями («главными румбами»). Для каждой точки земной поверхности главные направления занимают вполне определенное положение (рис. 2.2).
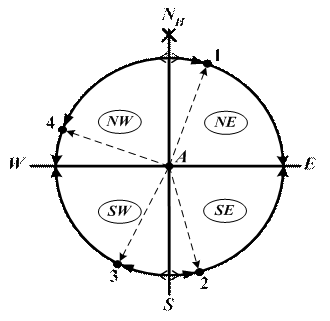
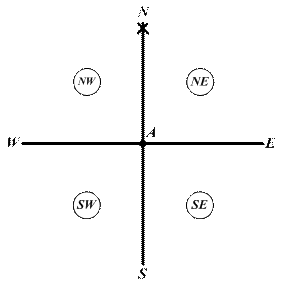
Рис. 2.2. Главные направления Главные направления делят плоскость ИГН на 4 равные четверти: NE, SE, SW, NW. Любое направление на поверхности Земли может быть измерено наблюдателем углом в плоскости ИГН от линии N-S меридиана. Для определения направлений в плоскости ИГН используются три системы деления горизонта, три системы счета направлений (круговая, полукруговая, четвертная). Рассмотрим эти системы.
Системы счета направлений Круговая система счета Круговая система счета направлений является основной системой счета. В этой системе горизонт делится на 360° (рис. 2.3) и счет направлений ведется от 0° до 360° от северной части истинного меридиана наблюдателя NИ вправо по ходу часовой стрелки.
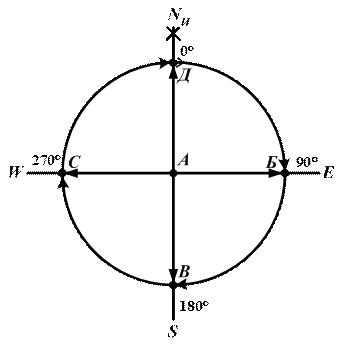
Рис. 2.3. Круговая система счета направлений
Наблюдатель (т. А) – в центре. Тогда направления: - на т. Б – 90°; - на т. В – 180°; - на т. С – 270°; - на т. Д – 360° или 0°. Если при расчете направлений получится значение более 360° (390°), то от результата следует вычесть 360° (т.е. один оборот 390° – 360° = 30°). Круговая система счета направлений применяется в судовождении для определения направления движения судна (курс) и определения направления с судна на береговые ориентиры, соседние суда и пр. (пеленг).
Полукруговая система счета
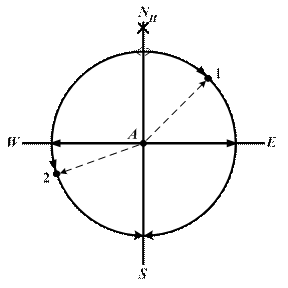
Рис. 2.4. Полукруговая система счета направлений
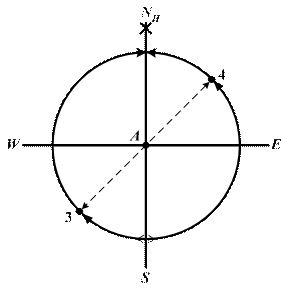
В полукруговой системе счета (рис. 2.4) счет направлений ведется от северной или южной части истинного меридиана наблюдателя в сторону востока Е или запада W в пределах от 0° до 180°. Для исключения многозначности в полукруговой системе счета числовому значению направления дается наименование. Например: т.1 N 45° E; т.2 N 105° W (рис. 2.4 а). т.3 S 45° W; т.4 S 135° E (рис. 2.4 б). Первая буква наименования – от какой части ИМН (N или S) идет счет. Вторая буква наименования – в каком направлении идет счет (к Е или к W). Полукруговая система счета обычно применяется в мореходной астрономии. Правила перехода от полукруговой с в мореходной астрономии.овому значению направления дается наименование. стока Е или запада ияесли при расчеьеесЕсли при расчетеистемы счета направлений в круговую:
Четвертная система счета
Рис. 2.5. Четвертая система счета направлений В четвертной системе счета направлений (рис. 2.5) счет направлений ведется от северной (N) и южной (S) части ИМН в сторону востока (Е) и в сторону запада (W) в пределах от 0° до 90°. В данной системе счета числовому значению направления дается наименование, соответствующее наименованию четверти. Например: т.1 10° NE; т.2 10° SE; т.3 30° SW; т.4 70° NW. Четвертная система счета направлений также будет нам встречаться при решении задач мореходной астрономии. Переход от четвертной системы счета к круговой аналогичен изложенному в п. Б, т.е.:
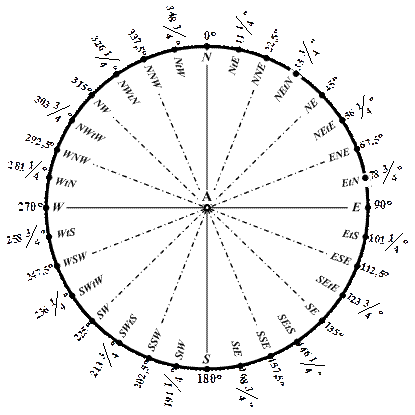
2.2.4. Румбовая система счета (рис. 2.6) Была основной системой счета направлений во времена парусного флота. Всего 32 румба -направления. 1 румб = 11¼° (11¼° ´ 32 = 360°).
Румбы в градусной мере (т. 41 «МТ-75», т. 5.13 «МТ-2000») Таблица 2.1
Главные румбы: N (0°), E (90°), S (180°), W (270°). Четвертные румбы: NЕ (45°), SE (135°), SW (225°), NW (315°). Вторые румбы: N NЕ (22,5°), S SE (157,5°), S SW (202,5°), N NW (337,5°). Шестые румбы: E NЕ (67,5°), E SE (112,5°), W SW (247,5°), W NW (292,5°). Нечетные румбы: NtE (11¼°), NEtE (56¼°) и т.д. Подробно см. табл. 41 «МТ-75» с. 311 или табл. 5.13 «МТ-2000» с. 435 (табл.2.1).
Рис. 2.6. Румбовая система счета направлений
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1913; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

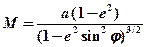 (1.4)
(1.4)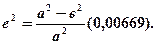
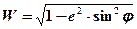 , то
, то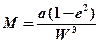 (1.5)
(1.5)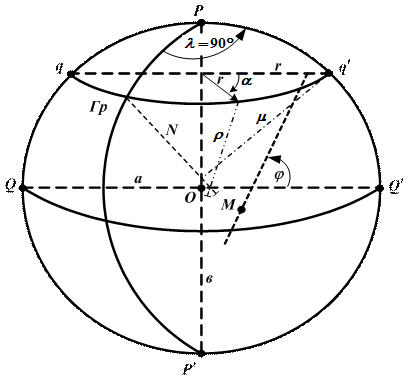
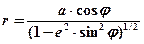 или
или 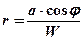 или
или 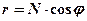 . (1.6)
. (1.6)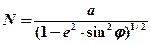 или
или 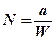 (1.7)
(1.7)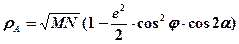 (1.8)
(1.8)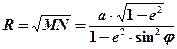 (1.9)
(1.9)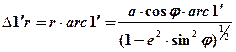 (1.10)
(1.10)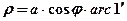 (1.11)
(1.11)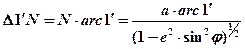 (1.12)
(1.12)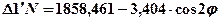 (1.13)
(1.13)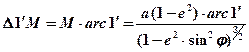 (1.14)
(1.14)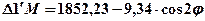 . (1.15)
. (1.15)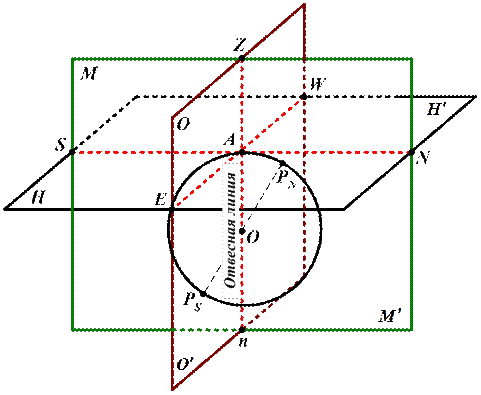
 а)
а)
 б)
б)