Система адмиралтейских номеров морских навигационных карт

 

Принцип построения проекции Меркатора

Картографические проекции и их классификация

Карта ® плоское, искаженное изображение земной поверхности, на котором искажения подчинены определенному математическому закону.

Положение любой точки на плоскости может быть определено пересечением двух координатных линий, которые однозначно соответствовали бы координатным линиям на Земле (j, l). Отсюда следует, что для получения плоского изображения земной поверхности нужно сначала нанести на плоскость систему координатных линий, которая соответствовала бы таким же линиям на сфере. Имея нанесенную на плоскость систему меридианов и параллелей, можно теперь нанести на эту сетку любые точки Земли.

Картографическая сетка ® условное изображение географической сетки земных меридианов и параллелей на карте в виде прямых или кривых линий.

Картографическая проекция ® способ построения картографической сетки на плоскости и изображение на ней сферической поверхности Земли, подчиненный определенному математическому закону.

Картографические проекции по характеру искажений делятся на:

1. Равноугольные (конформные) ® проекции, не искажающие углов. Сохраняется подобие фигур. Масштаб изменяется с изменением j и l. Отношение площадей не сохраняется (о. Гренландия» Африке, S_{Афр .} » 13,8 S_{о.Гренландия}).

2. Равновеликие (эквивалентные) ® проекции, на которых масштаб площадей везде одинаков и площади на картах пропорциональны соответствующим площадям в натуре. Равенства углов и подобия фигур не сохраняются. Масштаб длин в каждой точке не сохраняется по разным направлениям.

3. Произвольные ® проекции, заданные несколькими условиями, но не обладающие ни свойствами равноугольности, ни свойствами равновеликости. Ортодромическая проекция ® дуга большого круга изображается прямой линией.

Картографические проекции по способу построения картографической сетки делятся на:

1. Цилиндрические ® проекции, на которых картографическая сетка меридианов и параллелей получается путем проецирования земных координатных линий на поверхность цилиндра, касающегося условного глобуса (или секущего его), с последующей разверткой этого цилиндра на плоскость.

§ Прямая цилиндрическая проекция ® ось цилиндра совпадает с осью Земли;

§ Поперечная цилиндрическая проекция ® ось цилиндра перпендикулярна оси Земли;

§ Косая цилиндрическая проекция ® ось цилиндра расположена к оси Земли под углом отличным от 0° и 90°.

2. Конические ® проекции, на которых картографическая сетка меридианов и параллелей получается путем проецирования земных координатных линий на поверхность конуса, касающегося условного глобуса (или секущего его), с последующей разверткой этого конуса на плоскость. В зависимости от положения конуса относительно оси Земли различают:

§ Прямую коническую проекцию ® ось конуса совпадает с осью Земли;

§ Поперечную коническую проекцию ® ось конуса перпендикулярна оси Земли;

§ Косую коническую проекцию ® ось конуса расположена к оси Земли под углом отличным от 0° и 90°.

3. Азимутальные ® проекции, в которых меридианы – радиальные прямые, исходящие из одной точки (центральной), под углами равными соответствующим углам в натуре, а параллели ® концентрические окружности, проведенные из точки схождения меридианов (ортографические, внешние, стереографические, центральные, полярные, экваториальные, горизонтные).

 

Меркаторская проекция

Предложенная Меркатором проекция относится к разряду нормальных цилиндрических равноугольных проекций.

Карты, построенные в этой проекции, называются меркаторскими, а проекция ® проекция Меркатора или меркаторская проекция.

В меркаторской проекции все меридианы и параллели прямые и взаимноперпендикулярные линии, а линейная величина каждого градуса широты постепенно увеличивается с возрастанием широты, соответственно растягиванию параллелей, которые все в этой проекции по длине равны экватору.

Проекция Меркатора по характеру искажений относится к классу равноугольных.

Для получения морской навигационной карты в проекции Меркатора условный глобус помещают внутрь касательного цилиндра таким образом, чтобы их оси совпали.

Затем проецируют из центра глобуса меридианы на внутренние стенки цилиндра. При этом все меридианы изобразятся прямыми, параллельными между собой и перпендикулярными экватору линиями. Расстояния между ними равны расстояниям между теми же меридианами по экватору глобуса. Все параллели растянутся до величины экватора. При этом параллели, ближайшие к экватору, растянутся на меньшую величину и по мере удаления от экватора и приближения к полюсу величина их растяжения увеличивается.

Закон растяжения параллелей (рис. 6.1).

 

а)

б)

в)

 

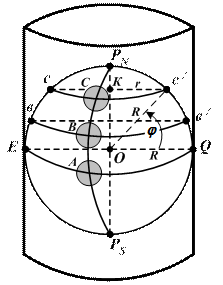
Рис. 6.1. Закон растяжения параллелей

 

R и r – радиус Земли и произвольной параллели (СС ¢).

j – широта произвольной параллели (СС ¢).

Из прямоугольного треугольника ОС ¢ К получим:

(6.4)

Обе части равенства умножим на 2 p, получим:

(6.5)

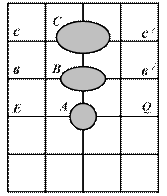
где 2 p × R – длина экватора;

2 p × r – длина параллели в широте j.

Следовательно, длина экватора равна длине соответствующей параллели, умноженной на секанс широты этой параллели. Все параллели, удлиняясь до длины экватора, растягиваются пропорционально sec j.

Разрезав цилиндр по одной из образующих, и развернув его на плоскость, получим сетку взаимно перпендикулярных меридианов и параллелей (рис. 6.1 б).

Эта сетка не удовлетворяет требованию равноугольности, т.к. изменились расстояния между меридианами по параллели, ибо каждая параллель растянулась и стала равной длине экватора. В результате фигуры с поверхности Земли перенесутся на сетку в искаженном виде. Углы в природе не будут соответствовать углам на сетке.

Очевидно, для того, чтобы не было искажений, т.е. чтобы сохранить на карте подобие фигур, а следовательно, и равенство углов, необходимо все меридианы в каждой точке растянуть на столько, на сколько растянулись в данной точке параллели, т.е. пропорционально sec j. При этом эллипс на проекции вытянется в направлении малой полуоси и станет кругом, подобным острову круглой формы на поверхности Земли. Радиус круга станет равным большой полуоси эллипса, т.е. будет в sec j раз больше круга на поверхности Земли (рис. 6.1 в).

Полученная таким образом картографическая сетка и проекция будут полностью удовлетворять требованиям, предъявленным к морским навигационным картам, т.е. проекцией Меркатора.