
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Числа, кодування і арифметична інформація.Содержание книги
Поиск на нашем сайте
Двійкові числа. Цифрові обчислювальні машини працюють з двійковими числами. Двійкова система зчислення або система з основою 2 використовує тільки цифри 0 і 1. Ці двійкові числа називаються бітами (від bi nary digi t). З фізичної точки зору в цифрових електронних системах біт 0 представлений напругою LOW (низьким), а біт 1 – напругою HIGH (високим). Людська діяльність припускає використання десяткової системи зчислення. Десяткова система, або система із основою 10, містить 10 цифр (від 0 до 9). Двійковій системі притаманна властивість врівноважування. Двійковому числу 10012 (читається: один, нуль, нуль, один) еквівалент 910 в десятковій. Біт одиниці двійкового числа називається молодшим бітом (МБ), біт вісімки – старшим бітом (СБ). Як перетворити двійкове число 1011 0110 (тобто: один, нуль, один, один, нуль, один, один, нуль) в його десятковий еквівалент? Процедура перетворення виконується у відповідності з табл.1.1. Десяткові значення кожної позиції записані під кожним бітом, потім десяткові числа підсумовуються (128+32+16+4+2=182), що дає 182. Таблиця 1.1 – Двійково-десяткові перетворення.
Зазвичай основа системи зчислення вказується індексами. Таким чином, число 1011 01102 є двійковим (тому що основа 2), а число 18210 – десятковим: 1011011012 = 18210. Як перетворити десяткове 155 в його двійковий еквівалент? Процедура перетворення приведена на рисунку 1.1.
Шістнадцяткові числа. Комірка пам’яті мікро – ЕОМ може містити двійкове число 10011110. Такий довгий ланцюжок нулів і одиниць складний для запам’ятовування і незручний для введення з клавіатури. Число 1001 1110 могло б бути перетворене в десяткове, що дало б 15810, але процес перетворення зайняв би багато часу. Більша частина систем мікроінформатики використовують шістнадцяткову форму запису, щоб спростити запам’ятовування і використання таких двійкових чисел, як 1001 1110. Шістнадцяткова система зчислення (hexadecimal), або система із основою 16, використовує 16 символів від 0 до 9 і А, B, C, D, E, F. Потрібно зауважити, що кожний шістнадцятковий символ може бути представлений єдиним сполученням чотирьох бітів. Таким чином, представленням двійкового числа 1001 1110 в шістнадцятковому коді є число 9Е. Це значить, що частина 1001 двійкового числа дорівнює 9, а друга частина 1110 дорівнює Е (звичайно, в шістнадцятковому коді). Звідси, 1001 11102 = 9Е16. (не слід забувати, що індекси означають основу системи зчислення). Як перетворити двійкове число 0111010 в шістнадцяткове? Потрібно розпочати з МБ і розділити двійкове число на групи із 4 бітів. Потім потрібно замінити кожну групу із 4 бітів еквівалентною шістнадцятковою цифрою: 10102 = А, 00112 = 3, звідси, 1110102 = 3 А16. Як перетворити шістнадцяткове число 7F в двійкове? В цьому випадку кожна шістнадцяткова цифра повинна бути замінена своїм двійковим еквівалентом з 4 біт. В прикладі двійкове число 0111 замінене шістнадцятковою цифрою 7, а 11112 замінене F16, звідки 7F16 = 011111112. Перетворимо шістнадцяткове число 2С6Е в десяткове. Процедурі дій перетворення відповідає табл. 1.2. Значення позицій перших чотирьох шістнадцяткових цифр є, відповідно, зліва направо 4096, 256, 16 і 1. Десяткове число містить 14 (Е16) одиниць, 6 чисел 16, 12 (С16) чисел 256 і 2 числа 4096. Кожна цифра множиться на відповідну її вагу, одержуємо суму, яка і дає нам десяткове число 11374. Таблиця 1.2 — Перетворення шістнадцяткового числа в десяткове
Перетворимо десяткове число 15797 в шістнадцяткове. На рис. 1.2. показна процедура дій. В першому рядку 1579710 розділено на 16, що дає часткове 98710 і залишок 510 який потім перетвориться в свій шістнадцяткових еквівалент (510=516) і стає цифрою молодшого розряду (МР) шістнадцяткового числа. Перше часткове (987) ділиться в другому рядку і знову ділиться на 16, що дає часткове і залишок 1110 або шістнадцяткове В. В третьому рядку 61 ділиться на 16, дає часткове 3 і залишок 1310 або D16 , а в четвертому рядку ділиться 3 на 16, дає часткове 0 і залишок 310 або 316. Коли часткове рівне 0, як в четвертому рядку, перетворення закінчується. 316 стає цифрою старшого розряду (СР) результату, тобто, 3DB516. Двійково-десяткові числа З метою зручності перетворення чисті двійкові числа представляються десятковими або шістнадцятковими. Однак, двійково-десяткове перетворення – операція не проста. В калькуляторах, магістралях і числових приладах, коли на доступних користувачу виходах і входах широко розповсюджені десяткові числа, для їх представлення використовують спеціальний двійково-десятковий код (ДДК). В табл. 1.3 наведено декілька десяткових чисел і відповідних їм двійково-десяткових еквівалентів (система 8421). Цим визначаються ваги позицій кожного з чотирьох бітів ДДК (використовують інші ДДК, наприклад 5421 і плюс 3).
Таблиця 1.3 – Двійково-десятковий код
Запишемо десяткове число 3691 в ДДК 8421. Кожна десяткова цифра перетворюється прямо в свій двійково-десятковий еквівалент із 4 бітів, і перетворення дають 369110=0011 0110 1001 0001ДДК. Перетворимо тепер двійково-десяткове число 1000000001110010 в його десятковий еквівалент. Кожна група із 4 бітів прямо перетворюється в її десятковий еквівалент, і тоді отримуємо 1000 0000 0111 0010ДДК = 807210: Мікропроцесори складають чисті двійкові числа, але вони мають, однак, команди для перетворення результату своїх складань в двійково-десяткове записування. Отримані двійково-десяткові числа легко потім представити в десятковому записі, використовуючи прості процедури, що були описані вище. Двійкова арифметика Додавання, віднімання або множення двійкових чисел виконується так само, як і в арифметиці двійкових чисел. Більшість мікропроцесорів мають команди додавання і віднімання двійкових чисел, однак деякі, менш багаточисельні виконують команди множення і ділення (наприклад, мікропроцесори INTEL 8086 і INTEL 8088). На рис.1.3, а запропоновані прості правила двійкового додавання. Два перших (зліва) правила очевидні, третє показує, що 1+1=10, тобто, найбільш значуща 1 переноситься в ближчий старший розряд. Четверте правило, на кінець, показує, що 1+1+1=11. В цьому випадку перший, другий доданки і запам’ятовувальне в результаті додавання в молодшому розряді число – все 1.
а – правило; б – приклад Рисунок 1.3 – Двійкове додавання Додамо двійкові числа 0011 1011 і 0010 1010 (операція показана на рис.1.4,б). Для великої ясності дії з десятковими еквівалентами, числа що оброблюються, показані на рисунку справа. Сумою двох чисел 0011 1011і 0010 1010 буде 0110 01012. На рис.1.4, а наведені правила двійкового віднімання. Перші три аналогічні десятковому розрахуванню. Останнє потребує займу з більш значущого попереднього розряду (в цьому випадку вага 2). Зменшувальним є двійкове число 10, від¢ємником 1, різницею – 1.
Віднімаємо двійкове число 0011 1001 від 0101 0101. Цей приклад наведений на рис.1.4, б. Розряди ваг 1, 2 і 4 цього двійкового обчислення прості для виконання і відносяться до перших трьох правил на рис.1.5, а. В колонці ваги 8 має місце віднімання 1 з 0. Тоді 1 запозичується із колонки ваги 16. Одиниця віднімається із 102, що дає різницю 1 згідно з четвертим правилом на рис. 1.5, а. Після цього запозичення в колонці ваги 16 має місце віднімання 1 з 0. Згідно з четвертим правилом 1 повинна бути запозичена із наступної, більш значущої позиції (колонка ваги 32), але в колонці 32 маємо 0; тому колонка 32 повинна запозичити з колонки ваги 64, що і зроблено. На кінець колонка 16 стає 102, від¢ємник 1, різниця 1. В колонці 32 маємо 1-1=0, в колонці 64 – 0-0=0, в колонці 128 – 0-0=0. таким часом, рис. 1.5,б ілюструє операцію обчислення 0011 10012 із 0101 01012 (справа ця задача вирішена в десятковому записі). Наведемо правила десяткового множення:
Два перших правила не потребують пояснення. В двох наступних множником є 1: коли множником є 1 при двійковому множенні, множене стає результатом і представляє собою добуток. Коли множник 0, добуток завжди 0. Виконаємо множення 1101 на 101. Як і у випадку множення десяткових чисел, множене спочатку множиться на число, що стоїть в молодшому розряді (у випадку, що розглядається – біт в колонці ваги 1). Оскільки біт множника в розряді ваги 1 є 1, множене копіюється і складає перший частковий добуток. Другим бітом множника є 0, тоді другий частковий добуток дорівнює 0000 (він зсунутий на одну позицію вліво). Бітом розряду ваги 4-го множника є 1, тоді для отримання третього часткового добутку знову слідує копіювання множеного (копіювання завершується новим зсувом на одну позицію вліво). Після цього виконуємо додавання трьох часткових добутків, що дає результат 11012´1012=10000012 відповідає добутку десяткових чисел 1310´510=6510.
Додатковий код. Сама ЕОМ оброблює інформацію, зазвичай, в двійковому коді. Однак, якщо потрібно використовувати цифри із знаком, використовують спеціальний додатковий код, що спрощує апаратні засоби ЕОМ. Звичайний регістр МП представляють простором із 8 бітів даних. Позиції бітів пронумеровані від 7 до 0, а ваги двійкових позицій вказані в основі регістра, біт 7 має вагу 128, біт 8 – 64 і так далі. В обох випадках біт 7 є знаковим. Він показує, чи є число додатним (+) або від’ємним (–). При 0 в знаковому біті число додатне, при 1 – від'ємне. Якщо число додатне, ті комірки пам’яті (6-0), що зосталися, містять двійкове 7–розрядне число. Наприклад, якщо регістр містить 0100 0001, це відповідає числу +6510 (64+1, знаковий біт додатний). Якщо в нього записано 0111 1111, буде містити +12710 (знаковий біт додатний: 0+64+32+16+8+4+2+1), що є найбільшим додатним числом, яке може містити 7-розрядний регістр. В табл. 1.4 наведений запис в додатковому коді додатних та від'ємних чисел. Всі додатні числа мають 0 в старшому біті, інші біти складають двійкове число. Всі від’ємні числа мають 1 в старшому розряді. Розглянемо рядок +0 в табл. 1.4: запис в додатковому коді +0 буде 0000 0000. В найближчому нижньому рядку бачимо, що запис в додатковому коді – 1 такий: 1111 1111. Розглянемо покрокове переміщення в зворотному напрямку від 0000 0000 до 1111 1111. Таблиця 1.4 — Десяткові числа із знаками і їх представлення в додатковому коді
Який буде запис в додатковому коді числа –9? Розглянемо етапи перетворення. Вони наведені в таблиці 1.5. Одержаний результат є додатковим кодом додатного десяткового числа. В наведеному прикладі додатковим кодом числа 9 є 1111 0111. Потрібно замітити, що знаковий біт 1, це означає, що дане число (1111 0111) від’ємне. Яким буде десятковий еквівалент числа 1111 0000, що записаний у формі додаткового коду? Процедура в цьому випадку наведена в таблиці 1.6. Таблиця 1.5 — Запис в додатковому коді числа мінус 9
Таблиця 1.6 — Десятковий еквівалент числа 1111 0000
Таким чином, формування зворотного коду і додавання 1 є тими ж процедурами, які ми проводили при перетворенні двійкового числа в додатковий код. Однак, слід відзначити, що хоча ми отримали двійкове число 0001 0000 = 1610, вихідний запис додаткового коду 1111 0000 = -16, тобто, маємо від’ємне число, оскільки старший біт в додатковому коді є 1.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 175; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.176.238 (0.008 с.) |






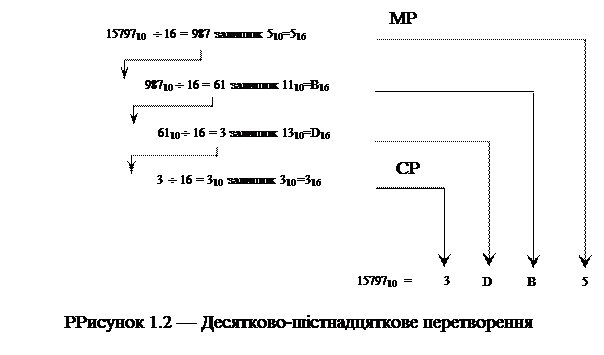

 1111 0111
1111 0111
 Двійкове число
Двійкове число



