
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Дослідження логічних елементів, логічні та арифметичні операції в двійковій системіСодержание книги
Поиск на нашем сайте Пішенін В.О., Нікітіна Н.В. Лабораторний практикум. У лабораторному практикумі розглянуто питання вивчення під час лабораторних робіт конструкції елементної бази електроніки, що використовується в технологічному обладнанні машинобудівних галузей промисловості. Наведені основні параметри та характеристики електронних приладів на основі напівпровідникових матеріалів. Зміст посібника відповідає програмі дисципліни "Електроніка і мікропроцесорна техніка", для студентів машинобудівних спеціальностей з питань використання електронної техніки у технологічному обладнанні та виробах машинобудівних галузей промисловості і застосування набутих знань у вивченні курсів дисциплін "Приводи верстатів та роботів" і "Приводи автоматизованого устаткування".
ЗМІСТ Лабораторна робота №1. 6 1.1 Тема: Дослідження логічних елементів, логічні та арифметичні операції в двійковій системі 6 1.2 Теоретичні відомості 6 Числа, кодування і арифметична інформація. 6 Шістнадцяткові числа. 7 Двійково-десяткові числа. 8 Двійкова арифметика. 10 Додатковий код. 12 1.3 Послідовність виконання роботи та зміст звіту. 14 1.4 Варіанти завдань. 15 ЛАБОРАТОРНА РОБОТА №2. 16 2.1 Тема: Дослідження та синтез комбінаційних схем управління. 16 2.2 Теоретичні відомості 16 Цифрові електронні і мікроелектронні пристрої 16 Дешифратори. 21 Шифратори. 22 Перетворювачі кодів. 22 Мультиплексор. 22 2.3 Хід роботи. 24 2.4 Зміст звіту. 24 2.5 Задача. 26 2.6 Варіанти завдань до задачі 27 ЛАБОРАТОРНА РОБОТА №3. 28 3.1 Тема: Синтез схеми управління технологічним обладнанням. 28 3.2 Теоретичні відомості 28 3.3 Хід роботи. 30 3.4 Зміст звіту. 31 3.4 Варіанти завдань. 32 ЛАБОРАТОРНА РОБОТА №4. 37 4.1 Тема: Вивчення апаратної частини мікро-ЕОМ.. 37 4.2 Порядок виконання роботи. 37 4.3 Методичні вказівки. 37 4.4 Варіанти завдань. 43 4.5 Зміст звіту. 44 ЛАБОРАТОРНА РОБОТА №5. 45 5.1 Тема: Програмування мікро – ЕОМ.. 45 5.2 Порядок виконання роботи. 45 5.3 Методичні вказівки. 45 Зміст звіту: 51 ЛАБОРАТОРНА РОБОТА №6. 52 6.1 Тема: Налагодження програми керування. 52 6.2 Порядок виконання роботи. 52 6.3 Методичні вказівки. 52 Складання програм для реалізації алгоритмів керування. 52 Демонстрація роботи програм викладачеві 57 Зміст звіту: 57 ЛАБОРАТОРНА РОБОТА №7. 58 7.1 Тема: Дослідження характеристик діода. 58 7.2 Теоретичні відомості 58 Напівпровідникові діоди. 58 Вольт-амперна характеристика діода. 58 7.3 Хід роботи. 64 Зміст звіту. 64 ЛАБОРАТОРНА РОБОТА №8. 65 8.1 Тема: Дослідження перехідних характеристик біполярного транзистора 65 8.2 Теоретичні відомості 65 Транзистори. 65 Основні процеси в транзисторі 66 8.3 Хід роботи. 69 Зміст звіту. 69 ЛІТЕРАТУРА.. 70
Даний лабораторний практикум призначений для методичного забезпечення дисципліни "Електроніка та мікропроцесорна техніка", що викладається студентам машинобудівних спеціальностей. Основним результатом успішного виконання запропонованих лабораторних робіт у першій частині практикуму є: закріплення теоретичного матеріалу відповідних розділів; набуття практичних навичок роботи з електронним обладнанням та обчислення основних характеристик електронних приладів та схем з їх застосуванням. На перших лекційних заняттях студенти отримують перелік тем лабораторних занять та список рекомендованої літератури. На першому лабораторному занятті студенти знайомляться з вимогами техніки безпеки та правилами протипожежної безпеки під час роботи з обладнанням лабораторій інституту і зобов'язаннями не порушувати встановлені правила, що підтверджується підписами у журналі з інструктажу відповідних лабораторій. Студент допускається до виконання лабораторної роботи при знанні мети, змісту роботи та методики її виконання. Якщо студент недостатньо підготовлений до виконання лабораторної роботи, то він повинен протягом 10... 15 хвилин підготуватися безпосередньо в класі, отримуючи вказівки від викладача. Захист лабораторної роботи відбувається протягом 15 хвилин групами по декілька студентів шляхом пред'явлення звіту з лабораторної роботи та відповідей на питання викладача безпосередньо на робочих місцях (за комп'ютерами) або поза робочих місць за рішенням викладача. Звіти з лабораторних робіт попередньо оформлюються в електронному варіанті, а потім за рішенням викладача роздруковуються для набуття навичок у оформленні документації з використанням комп'ютерних технологій (там, де це потрібно). Звіт з лабораторної роботи виконується на аркушах формату А4 (210´297мм) на одному боці аркуша з дотриманням вимог стандарту ДСТУ 3008–95. При оформленні звіту необхідно дотримуватися такої послідовності викладення: ¾ назва лабораторної роботи; ¾ мета лабораторної роботи; ¾ завдання роботи; ¾ теоретична частина; ¾ описання ходу виконання та отриманих результатів при цьому; ¾ висновки. Лабораторна робота №1 Тема: Дослідження логічних елементів, логічні та арифметичні операції в двійковій системі Мета роботи: знайомство з одно- та двомісними функціями, придбання практичних навичок з синтезу комбінаційних схем, засвоєння форм представлення цифрової інформації та операції з її перетворення. Обладнання: комплект логічних елементів, блок живлення, логічний пробник. Теоретичні відомості Шістнадцяткові числа. Комірка пам’яті мікро – ЕОМ може містити двійкове число 10011110. Такий довгий ланцюжок нулів і одиниць складний для запам’ятовування і незручний для введення з клавіатури. Число 1001 1110 могло б бути перетворене в десяткове, що дало б 15810, але процес перетворення зайняв би багато часу. Більша частина систем мікроінформатики використовують шістнадцяткову форму запису, щоб спростити запам’ятовування і використання таких двійкових чисел, як 1001 1110. Шістнадцяткова система зчислення (hexadecimal), або система із основою 16, використовує 16 символів від 0 до 9 і А, B, C, D, E, F. Потрібно зауважити, що кожний шістнадцятковий символ може бути представлений єдиним сполученням чотирьох бітів. Таким чином, представленням двійкового числа 1001 1110 в шістнадцятковому коді є число 9Е. Це значить, що частина 1001 двійкового числа дорівнює 9, а друга частина 1110 дорівнює Е (звичайно, в шістнадцятковому коді). Звідси, 1001 11102 = 9Е16. (не слід забувати, що індекси означають основу системи зчислення). Як перетворити двійкове число 0111010 в шістнадцяткове? Потрібно розпочати з МБ і розділити двійкове число на групи із 4 бітів. Потім потрібно замінити кожну групу із 4 бітів еквівалентною шістнадцятковою цифрою: 10102 = А, 00112 = 3, звідси, 1110102 = 3 А16. Як перетворити шістнадцяткове число 7F в двійкове? В цьому випадку кожна шістнадцяткова цифра повинна бути замінена своїм двійковим еквівалентом з 4 біт. В прикладі двійкове число 0111 замінене шістнадцятковою цифрою 7, а 11112 замінене F16, звідки 7F16 = 011111112. Перетворимо шістнадцяткове число 2С6Е в десяткове. Процедурі дій перетворення відповідає табл. 1.2. Значення позицій перших чотирьох шістнадцяткових цифр є, відповідно, зліва направо 4096, 256, 16 і 1. Десяткове число містить 14 (Е16) одиниць, 6 чисел 16, 12 (С16) чисел 256 і 2 числа 4096. Кожна цифра множиться на відповідну її вагу, одержуємо суму, яка і дає нам десяткове число 11374. Таблиця 1.2 — Перетворення шістнадцяткового числа в десяткове
Перетворимо десяткове число 15797 в шістнадцяткове. На рис. 1.2. показна процедура дій. В першому рядку 1579710 розділено на 16, що дає часткове 98710 і залишок 510 який потім перетвориться в свій шістнадцяткових еквівалент (510=516) і стає цифрою молодшого розряду (МР) шістнадцяткового числа. Перше часткове (987) ділиться в другому рядку і знову ділиться на 16, що дає часткове і залишок 1110 або шістнадцяткове В. В третьому рядку 61 ділиться на 16, дає часткове 3 і залишок 1310 або D16 , а в четвертому рядку ділиться 3 на 16, дає часткове 0 і залишок 310 або 316. Коли часткове рівне 0, як в четвертому рядку, перетворення закінчується. 316 стає цифрою старшого розряду (СР) результату, тобто, 3DB516. Двійково-десяткові числа З метою зручності перетворення чисті двійкові числа представляються десятковими або шістнадцятковими. Однак, двійково-десяткове перетворення – операція не проста. В калькуляторах, магістралях і числових приладах, коли на доступних користувачу виходах і входах широко розповсюджені десяткові числа, для їх представлення використовують спеціальний двійково-десятковий код (ДДК). В табл. 1.3 наведено декілька десяткових чисел і відповідних їм двійково-десяткових еквівалентів (система 8421). Цим визначаються ваги позицій кожного з чотирьох бітів ДДК (використовують інші ДДК, наприклад 5421 і плюс 3).
Таблиця 1.3 – Двійково-десятковий код
Запишемо десяткове число 3691 в ДДК 8421. Кожна десяткова цифра перетворюється прямо в свій двійково-десятковий еквівалент із 4 бітів, і перетворення дають 369110=0011 0110 1001 0001ДДК. Перетворимо тепер двійково-десяткове число 1000000001110010 в його десятковий еквівалент. Кожна група із 4 бітів прямо перетворюється в її десятковий еквівалент, і тоді отримуємо 1000 0000 0111 0010ДДК = 807210: Мікропроцесори складають чисті двійкові числа, але вони мають, однак, команди для перетворення результату своїх складань в двійково-десяткове записування. Отримані двійково-десяткові числа легко потім представити в десятковому записі, використовуючи прості процедури, що були описані вище. Двійкова арифметика Додавання, віднімання або множення двійкових чисел виконується так само, як і в арифметиці двійкових чисел. Більшість мікропроцесорів мають команди додавання і віднімання двійкових чисел, однак деякі, менш багаточисельні виконують команди множення і ділення (наприклад, мікропроцесори INTEL 8086 і INTEL 8088). На рис.1.3, а запропоновані прості правила двійкового додавання. Два перших (зліва) правила очевидні, третє показує, що 1+1=10, тобто, найбільш значуща 1 переноситься в ближчий старший розряд. Четверте правило, на кінець, показує, що 1+1+1=11. В цьому випадку перший, другий доданки і запам’ятовувальне в результаті додавання в молодшому розряді число – все 1.
а – правило; б – приклад Рисунок 1.3 – Двійкове додавання Додамо двійкові числа 0011 1011 і 0010 1010 (операція показана на рис.1.4,б). Для великої ясності дії з десятковими еквівалентами, числа що оброблюються, показані на рисунку справа. Сумою двох чисел 0011 1011і 0010 1010 буде 0110 01012. На рис.1.4, а наведені правила двійкового віднімання. Перші три аналогічні десятковому розрахуванню. Останнє потребує займу з більш значущого попереднього розряду (в цьому випадку вага 2). Зменшувальним є двійкове число 10, від¢ємником 1, різницею – 1.
Віднімаємо двійкове число 0011 1001 від 0101 0101. Цей приклад наведений на рис.1.4, б. Розряди ваг 1, 2 і 4 цього двійкового обчислення прості для виконання і відносяться до перших трьох правил на рис.1.5, а. В колонці ваги 8 має місце віднімання 1 з 0. Тоді 1 запозичується із колонки ваги 16. Одиниця віднімається із 102, що дає різницю 1 згідно з четвертим правилом на рис. 1.5, а. Після цього запозичення в колонці ваги 16 має місце віднімання 1 з 0. Згідно з четвертим правилом 1 повинна бути запозичена із наступної, більш значущої позиції (колонка ваги 32), але в колонці 32 маємо 0; тому колонка 32 повинна запозичити з колонки ваги 64, що і зроблено. На кінець колонка 16 стає 102, від¢ємник 1, різниця 1. В колонці 32 маємо 1-1=0, в колонці 64 – 0-0=0, в колонці 128 – 0-0=0. таким часом, рис. 1.5,б ілюструє операцію обчислення 0011 10012 із 0101 01012 (справа ця задача вирішена в десятковому записі). Наведемо правила десяткового множення:
Два перших правила не потребують пояснення. В двох наступних множником є 1: коли множником є 1 при двійковому множенні, множене стає результатом і представляє собою добуток. Коли множник 0, добуток завжди 0. Виконаємо множення 1101 на 101. Як і у випадку множення десяткових чисел, множене спочатку множиться на число, що стоїть в молодшому розряді (у випадку, що розглядається – біт в колонці ваги 1). Оскільки біт множника в розряді ваги 1 є 1, множене копіюється і складає перший частковий добуток. Другим бітом множника є 0, тоді другий частковий добуток дорівнює 0000 (він зсунутий на одну позицію вліво). Бітом розряду ваги 4-го множника є 1, тоді для отримання третього часткового добутку знову слідує копіювання множеного (копіювання завершується новим зсувом на одну позицію вліво). Після цього виконуємо додавання трьох часткових добутків, що дає результат 11012´1012=10000012 відповідає добутку десяткових чисел 1310´510=6510.
Додатковий код. Сама ЕОМ оброблює інформацію, зазвичай, в двійковому коді. Однак, якщо потрібно використовувати цифри із знаком, використовують спеціальний додатковий код, що спрощує апаратні засоби ЕОМ. Звичайний регістр МП представляють простором із 8 бітів даних. Позиції бітів пронумеровані від 7 до 0, а ваги двійкових позицій вказані в основі регістра, біт 7 має вагу 128, біт 8 – 64 і так далі. В обох випадках біт 7 є знаковим. Він показує, чи є число додатним (+) або від’ємним (–). При 0 в знаковому біті число додатне, при 1 – від'ємне. Якщо число додатне, ті комірки пам’яті (6-0), що зосталися, містять двійкове 7–розрядне число. Наприклад, якщо регістр містить 0100 0001, це відповідає числу +6510 (64+1, знаковий біт додатний). Якщо в нього записано 0111 1111, буде містити +12710 (знаковий біт додатний: 0+64+32+16+8+4+2+1), що є найбільшим додатним числом, яке може містити 7-розрядний регістр. В табл. 1.4 наведений запис в додатковому коді додатних та від'ємних чисел. Всі додатні числа мають 0 в старшому біті, інші біти складають двійкове число. Всі від’ємні числа мають 1 в старшому розряді. Розглянемо рядок +0 в табл. 1.4: запис в додатковому коді +0 буде 0000 0000. В найближчому нижньому рядку бачимо, що запис в додатковому коді – 1 такий: 1111 1111. Розглянемо покрокове переміщення в зворотному напрямку від 0000 0000 до 1111 1111. Таблиця 1.4 — Десяткові числа із знаками і їх представлення в додатковому коді
Який буде запис в додатковому коді числа –9? Розглянемо етапи перетворення. Вони наведені в таблиці 1.5. Одержаний результат є додатковим кодом додатного десяткового числа. В наведеному прикладі додатковим кодом числа 9 є 1111 0111. Потрібно замітити, що знаковий біт 1, це означає, що дане число (1111 0111) від’ємне. Яким буде десятковий еквівалент числа 1111 0000, що записаний у формі додаткового коду? Процедура в цьому випадку наведена в таблиці 1.6. Таблиця 1.5 — Запис в додатковому коді числа мінус 9
Таблиця 1.6 — Десятковий еквівалент числа 1111 0000
Таким чином, формування зворотного коду і додавання 1 є тими ж процедурами, які ми проводили при перетворенні двійкового числа в додатковий код. Однак, слід відзначити, що хоча ми отримали двійкове число 0001 0000 = 1610, вихідний запис додаткового коду 1111 0000 = -16, тобто, маємо від’ємне число, оскільки старший біт в додатковому коді є 1. Варіанти завдань
ЛАБОРАТОРНА РОБОТА №2 Теоретичні відомості Дешифратори Це перетворювачі кодів, що виконують перетворення двійкового і двійково-десяткового кодів в унітарний код. Унітарний код двійкового n-розрядного числа представляється 2n розрядами, один із розрядів якого рівний 1. Дешифратори можуть бути повними і неповними. Повним дешифратором називається комбінаційна схема, що має n входів і 2n виходів і що реалізує на кожному виході функцію, яка представляє собою конституенту одиниці (мінтерм). Він описується системою із 2n логічних рівнянь, права частина кожного із яких записується у вигляді конституенти одиниці. Наприклад, для двовхідного дешифратора:
Схема, що реалізує цю функцію, показана на рисунку 2.5, а, а її умовне позначення – на рисунку 2.5, б. На лівому полі показані ваги вхідних сигналів х0 і х1, комбінації значень яких розглядаються в якості двійкових чисел. Кожному вхідному двійковому числу відповідає сигнал, рівний 1 тільки на виході, номер якого, вказаний на правому полі, збігається з двійковим числом. Неповний дешифратор реалізує m<2n конституент одиниці. Такі дешифратори використовуються, наприклад, для перетворення двійково-десяткового числа в код, призначений для керування десятковим індикатором (дешифратор 4´10). Приклад такого дешифратора (мікросхеми 155ИДІ та 564ИДІ) показані на рисунку 2.5, в. Як і для повного дешифратора, можна записати рівняння, що описує роботу неповного дешифратора, і за ним отримати логічну схему.
Найбільш розповсюджені мікросхеми дешифраторів К155ИД1, 3, 4, 10; К555, 6, 7, 10; К531ИЛД14. Шифратори Виконують функцію, зворотну дешифраторам, тобто, перетворюють унітарний код в двійковий, двійково-десятковий або будь-який інший. Робота шифратора, як будь-якої двійкової системи, може бути задана у вигляді таблиці відповідностей, за якою досить просто побудувати схему. Із мікросхем шифраторів відомі, наприклад, К555ИВ3, КМ555ИАІ. Перетворювачі кодів Вони використовують спільну роботу дешифратора і шифратора. Дешифратор перетворює двійковий або двійково-десятковий код в унітарний, а шифратор – отриманий унітарний код в потрібний. Типовим прикладом використання такого перетворювача є схема перетворення коду в код керування семисегментним індикатором. Мультиплексор Це схема, що має n + 2 n входів і один вихід, де n – число адресних, а 2n – число інформаційних входів. Призначення мультиплексорів (від англ. multiplex – багатократний) – комутувати в бажаному порядку інформацію, що надходить з декількох вхідних шин на одну вихідну. За допомогою мультиплексора здійснюється тимчасове розділення інформації, що надходить по різних каналах. Його можна уподібнити безконтактному багатопозиційному перемикачу. Мультиплексори мають дві групи входів або один, частіше два, що взаємодоповнюються (інверсні) виходи. Одні входи інформаційні, а інші служать для керування. До них відносяться адресні і розв'язувальні. Адреса представляється в двійковому коді, причому кожній адресі відповідає інформаційний вхід, сигнал з якого (0 або 1) при даній адресі приходить на вихід. Таким чином, в мультиплексорі здійснюється 2n вхідних сигналів на один вихід. Розв'язувальний вхід керує одночасно всіма інформаційними входами незалежно від стану адресних входів. Заперечувальний сигнал на цьому вході блокує дію всього пристрою. Наявність розв'язувального входу розширює функціональні можливості мультиплексора, дозволяє синхронізувати його роботу з роботою інших вузлів. Цей вхід використовується також для нарощування розрядності мультиплексорів. У мультиплексорі, що виготовляється у вигляді окремих мікросхем, число інформаційних входів не перевищує 16. Більша кількість входів забезпечується шляхом нарощування. Нарощування можна виконувати об¢єднанням декількох мультиплексорів в пірамідоподібну (деревовидну) систему або послідовним з¢єднанням розв'язувальних входів і зовнішніх логічних елементів. Другий спосіб застосовується частіше за все, оскільки при пірамідоподібному нарощуванні більші витрати мікросхем і порівняно низька швидкодія через підсумовування затримок при послідовному проходженні сигналів за ступеням піраміди.
Для отримання 64–канального мультиплексора слід використовувати чотири БИС155КП1 і 4–вхідний елемент І–НІ, а керування входами Хід роботи 2.3.1 Від аналітичного завдання комбінаційної ф-ї (n=3) перейти до словесного та табличного, здійснити оптимізацію ф-ї двома методами: а) за допомогою діаграми Вейча-Карно; б) алгебраїчним методом на підставі законів алгебри Буля. Розробити комбінаційні схеми для вихідного та мінімізованого варіантів ф-ї на І, АБО, НІ. 2.3.2 Від матричного задання комбінаційної ф-ї (n=4) перейти до її аналітичного запису, виконати мінімізацію ф-ї, розробити комбінаційну схему в двох варіантах: а) на елементах І-НІ, АБО-НІ; б) на елементах І, АБО, НІ. Вибрати оптимальний варіант за кількістю елементів потрібних для реалізації схем. Реалізувати комбінаційну схему, що розроблена на попередній лабораторній роботі, користуючись універсальною монтажною платою; підключити схему до блока живлення, дослідити її функціонування, скласти таблицю відповідностей. Зміст звіту 2.4.1 Наприклад, задано комбінаційну ф-ю трьох аргументів F=
Х2
n=3 Мінімізація за допомогою діаграми Вейча-Карно F =
Розробляємо комбінаційну схему для мінімізованої ф-ї Варіанти завдань до задачі
ЛАБОРАТОРНА РОБОТА №3 Теоретичні відомості У відповідності з етапами синтезу автомата студент виконує такі формалізаційні процедури. 3.2.1 Розмітка граф-схеми алгоритму (ГСА). Розмітка виконується для моделі автомата Мілі. Відмічаються входи всіх вершин, що слідують за операторними вершинами. При цьому входи в кінцеву вершину і у вершину, що слідує за начальною, відмічаються як вихідний стан автомата (а1). 3.2.2 Отримання автоматного графа.
3.2.3 Кодування станів автомата За числом станів автомата визначають кількість тригерів для його пам¢яті. N = Int (log2M) + 1 Кожному стану автомата ставиться у відповідність певний код, який відображає комбінацію вмикання тригерів пам¢яті. Вихідному стану автомата завжди відповідає загальне скидання тригерів. Наприклад:
3.2.4 Побудова структурної схеми автомата з обраним типом тригерів (тригери з розділювальними входами, з лічильним входом або D-тригери). 3.2.5 Отримання структурних формул для керуючих сигналів У на об¢єкт керування і сигналів збудження пам¢яті. Структурні формули отримуються безпосередньо з автоматного графа. Кількість доданків у формулі по кожному сигналу визначається числом його появ у автоматному графі. Так, з вищенаведеного фрагмента графа: У1=а3Х2 У1= Т1Т2Т1Х2 У2 = а3Х2Vа3Х2 або У2=Т3Т2Т1Х2VТ3Т2Т1Х2 У4=аХ2 У4=Т3Т2Т1Х2 Сигнали збудження пам¢яті залежать від типу тригерів. Так, сигнал S вмикає тригер з розділювальними входами, а сигнал R вимикає його. Тригер з лічильним входом перемикається сигналом S у протилежний стан, а D-тригер вмикається сигналом S на один такт автоматного часу. Сигнали збудження пам¢яті проставляються в автоматному графі біля загострення стрілок поруч з керуючими сигналами. Так, для вищенаведеного фрагмента у випадку тригерів з розділювальними входами:
R2 = a3X2 або R2 = Т3Т2Т1Х2 S3 = а3Х2Vа3Х2 S3 = Т3Т2Т1Х2VТ3Т2Т1Х2 3.2.6 Побудова схеми автомата. Принципова схема цифрового автомата отримується зі структурних формул за конфігурацією його структурної схеми. Схема повинна мати канонічну структуру – чіткі вертикальні ряди однотипних елементів: правий – тригери; лівіший – логічні елементи АБО; ще лівіше – логічні елементи І; ще лівіше – інвертори (при необхідності). 3.2.7 Набір схеми автомата на демонстраційному планшеті проводиться у відповідності до методичних вказівок для роботи з планшетом. Хід роботи 3.3.1 Ознайомитись з блок-схемою алгоритму роботи системи управління; при цьому з’ясувати: кількість сигналів, що генерується схемою; кількість вхідних сигналів; загальний характер алгоритму — лінійний чи розгалужений. 3.3.2 Виконати розмітку блок-схеми з метою подальшої розробки графа переходів. За прийнятою методикою, вершини графа розміщуються на входах умовних операторів і позначаються кружками на відповідних місцях блок-схеми алгоритму. 3.3.3 Виконати розмітку блок-схеми. Попередньо розробити граф переходів. Спочатку зображується те, що входить до основного (лінійного) циклу. Вершини графа розміщуємо так, щоб вони утворили коло (еліпс). Вершини графа з’єднують стрілками, що символізують такти, тобто переходи з попереднього стану в наступний. Біля вістря стрілки пишуть сигнали управління, а біля початку стрілки пишуть сигнали від датчиків. Передбачаємо далі тригери для шифрування кожної вершини (стану), кількість необхідних для цього тригерів визначається за формулою: N=TRUNC(LOG2M)+1, де М-кількість вершин графа. Кожному стану автомата (вершини графа) привласнюється певний код. На графі переходів указують також стрілки, що відповідають основним переходом. 3.3.4 Остаточно оформити граф-переходів, додаючи до вихідних технологічних сигналів, сигнали управління тригерами. 3.3.5 Написати булеві функції для сигналів керування: — технологічним обладнанням; — тригерами пам’яті. Ці функції складаються з графа переходів – диз’юнкція, кон’юнкція при цьому кількість додатків формули визначається числом появ розглядуваного сигналу протягом робочого циклу автомата. 3.3.6 Розробити принципіальну схему керування. При цьому слід дотримуватися канонічного вигляду таких схем: ліворуч розташована шина вхідних сигналів: поруч розміщено кон’юнктори. Далі креслимо диз’юнктори в кількості відповідно до кількості сигналів. Праворуч на схемі зображаються тригери шифрації стану та диз’юнктори керування цими тригерами. Задачі диз’юнкції також слід підключити до кон’юнкторів умов переходу. 3.3.7 Перевірити складену схему за такими параметрами: — правильність підключення кон’юнкторів сигналів переходів до шини вхідних даних; — правильність підключення диз’юнкторів сигналів керування технологічним обладнанням; — правильність підключення диз’юнкторів сигналів керування тригерами пам’яті. 3.3.8 Набрати синтезовану схему управління на універсал
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.255.225 (0.016 с.) |





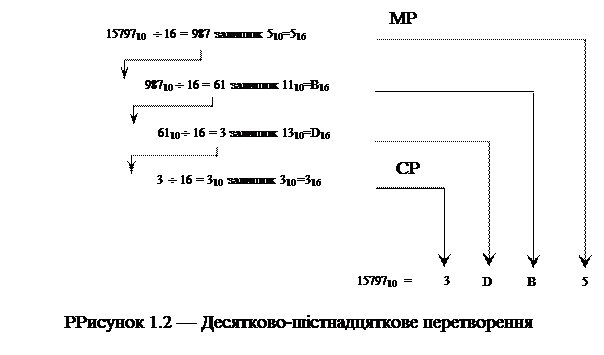

 1111 0111
1111 0111
 Двійкове число
Двійкове число



 необхідно виконувати інверсним чотирирозрядним унітарним кодом.
необхідно виконувати інверсним чотирирозрядним унітарним кодом.



 ;
; ;
;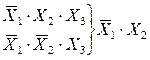 .
.










