
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Цифрові електронні і мікроелектронні пристроїСодержание книги
Поиск на нашем сайте
Комбінаційними логічними пристроями (КЛП) називаються такі пристрої, сигнали на виходах яких в будь-який момент часу однозначно визначаються додаванням сигналів на вході і не залежать від попередніх станів. Прикладами комбінаційних схем можуть служити логічні елементи, електронні ключі а також більш складніші пристрої, що виконують довільні логічні функції, функції шифраторів, дешифраторів, мультиплексорів, демультиплексорів, арифметичних пристроїв і т.п. Довільна комбінаційна логічна функція (КЛФ) може бути достатньо просто описана і синтезована за допомогою відомих методів, серед яких частіше за все використовуються карти Карно. Синтез комбінаційних схем з одним виходом можна розбити на три етапи. На першому етапі, виходячи із таблиць відповідності (істинності), описують роботу синтезованого КЛП, знаходять мінімальну диз’юнктивну (МДНФ) або мінімальну кон’юнктивну (МКНФ) форму функції. На другому етапі отриману МДНФ або МКНФ функції записують в операторній формі, де під оператором розуміють функцію, що реалізується конкретним логічним елементом. За операторною формою достатньо просто скласти схему КЛП. Розглянемо основні операторні форми на прикладі Різні операторні форми легко отримати із МДНФ і МКНФ шляхом елементарних логічних перетворювань. Так, взявши подвійне заперечення від МДНФ функції і використовуючи правило де Моргана, отримаємо для нашого прикладу такі операційні форми:
=
Для отримання інших оперативних форм функцію записують в МКНФ, тобто її інверсне значення:
Виконавши попередні перетворення, отримаємо:
На заключному третьому етапі за операторними уявленнями функції складається комбінаційна схема. Методи синтезу КЛП з декількома виходами основані на використанні однієї функції або її частини для отримання іншої функції. При цьому дублювання логічних елементів практично відсутнє. Найбільш простіше синтез таких КЛП здійснюється за допомогою діаграми Вейча або карти Карно, які для кожної функції будуються окремо, а потім на них відмічаються однойменні набори, на яких всі або декілька функцій приймають однакові значення. Розглянемо методику і приклад синтезу довільної комбінаційної логічної схеми з врахуванням реального базису логічних елементів: а) логічна функція, у відповідності до якої буде працювати розроблювана схема, що задана в словесному чи іншому вигляді, записується в формі, зручній для подальшого синтезу, краще всього у вигляді таблиці відповідностей (істинності). Для наочної ілюстрації скористуємося конкретним прикладом, що заданий в таблиці 2.1. Ця таблиця відповідності чотиримісної функції, де на кожному із номерів 0...15 задано значення функції (знаком Æ позначені невизначені стани). Таблиця 2.1 — Відповідність чотиримісної функції
б) За табл. 2.1. і карті Вейча для чотирьох змінних (рис. 2.1, а) функція наноситься на карту Вейча (рис. 2.1, б)
г) Записується результат покриттів у вигляді диз’юнкції кон’юнкцій:
Отримане рівняння є основою для побудови електричної схеми, що реалізує задану логічну функцію, однак не враховує характеристики реальних логічних елементів, що є в лабораторії. Аналізуючи отриману функцію, необхідно підібрати реальні логічні елементи для її реалізації. Так, в нашому прикладі необхідно один чотиривхідний, два тривхідних, два двовхідних елементи і чотири інвертори на кожну із змінних. В якості логічних елементів зручно використовувати елементи К155ЛА1, К155ЛА4, К155ЛА3, що реалізують функції І–НІ, тому запишемо функцію F(7/1) в системі І-НІ:
Для реалізації цієї функції вибирають: 1) один корпус мікросхеми К155ЛА3 (або один корпус мікросхеми К155ЛН1), елемент DD1 (рис.2.1, в), що дозволяє при об’єднаних входах кожного логічного елемента реалізувати інверсію всіх чотирьох змінних; 2) один корпус мікросхеми К155ЛА4 (елемент DD2), що дозволяє реалізувати дві тривхідні функції І–НІ і на тій мікросхемі, що залишилася вільною, одну двовхідну функцію І–НІ (об’єднавши два її входи); 3) один корпус мікросхеми К155ЛА1 (елемент DD3), що дозволяє реалізувати на одній своїй половині чотиривхідну функцію І–НІ, а на другій – двовхідну функцію І–НІ, об¢єднавши попарно їх входи; д) у відповідності з формулою логічної функції (2.1) і вибраними елементами DD1, DD2 і DD3 будується принципіальна схема (рис. 2.1, в), на якій жирною лінією показана загальна шина, номери вхідних сигналів якої позначають числами зліва, а вихідних – справа. Наприклад, якщо сигнал х1позначений індексом 3 (рисунок 2.1, в), то із рисунку видно, що він поступає на входи 2, 9 і 10 елемента DD2. Аналогічно позначають і інші сигнали. Застосування такого позначення суттєво спрощує зображення і читання схем. Спеціальні КЛП призначені для реалізації конкретних логічних функцій: підсумовування, шифрування, дешифрування, перетворення кодів та інші операції. В той же час вони можуть бути реалізовані і на універсальних логічних елементах. Розглянемо основні види цих схем і особливості їх реалізації. Суматори. Це пристрої, що здійснюють основну арифметичну операцію — підсумовування чисел в двійковому коді. Найпростіший випадок — підсумовування двох однорозрядних чисел: 0 + 0 = 0, 1 + 0 =1, 1 + 1 = 10. В останньому випадку вихідне число 10 (в десятковому записі це 2) виявилося двійковим дворозрядним. Одиниця, що з¢явилася в старшому розряді суми, називається одиницею переносу. На рис. 2.2, а, б показані схема і таблиця для підсумовування двох однорозрядних чисел. Схема складається із елементів нерівнозначності (що виключають АБО) і елементів І і має два вихідних проводи: суми S i і переносу Р і. Така схема називається півсуматором.
Повний суматор повинен додатково мати вхід для прийому сигналу переносу Рі-1 попереднього розряду. Схема повного суматора двох однорозрядних чисел на двох півсуматорах і його таблиця відповідностей показана на рисунку 2.3, а, б.
а)
б) Рисунок 2.3 — Схема повного суматора Повні суматори багаторозрядних чисел складаються із однорозрядних. Чотирирозрядний паралельний суматор показаний на рисунку 2.4. Тут порозрядно (по паралелі) підсумовуються два чотирирозрядні слова. Ці пристрої можна зробити довільної довжини, однак підсумовування буде закінчене лише тоді, коли закінчиться час розповсюдження сигналів переносу Рі через весь ланцюг однорозрядних суматорів.
Дешифратори Це перетворювачі кодів, що виконують перетворення двійкового і двійково-десяткового кодів в унітарний код. Унітарний код двійкового n-розрядного числа представляється 2n розрядами, один із розрядів якого рівний 1. Дешифратори можуть бути повними і неповними. Повним дешифратором називається комбінаційна схема, що має n входів і 2n виходів і що реалізує на кожному виході функцію, яка представляє собою конституенту одиниці (мінтерм). Він описується системою із 2n логічних рівнянь, права частина кожного із яких записується у вигляді конституенти одиниці. Наприклад, для двовхідного дешифратора:
Схема, що реалізує цю функцію, показана на рисунку 2.5, а, а її умовне позначення – на рисунку 2.5, б. На лівому полі показані ваги вхідних сигналів х0 і х1, комбінації значень яких розглядаються в якості двійкових чисел. Кожному вхідному двійковому числу відповідає сигнал, рівний 1 тільки на виході, номер якого, вказаний на правому полі, збігається з двійковим числом. Неповний дешифратор реалізує m<2n конституент одиниці. Такі дешифратори використовуються, наприклад, для перетворення двійково-десяткового числа в код, призначений для керування десятковим індикатором (дешифратор 4´10). Приклад такого дешифратора (мікросхеми 155ИДІ та 564ИДІ) показані на рисунку 2.5, в. Як і для повного дешифратора, можна записати рівняння, що описує роботу неповного дешифратора, і за ним отримати логічну схему.
Найбільш розповсюджені мікросхеми дешифраторів К155ИД1, 3, 4, 10; К555, 6, 7, 10; К531ИЛД14. Шифратори Виконують функцію, зворотну дешифраторам, тобто, перетворюють унітарний код в двійковий, двійково-десятковий або будь-який інший. Робота шифратора, як будь-якої двійкової системи, може бути задана у вигляді таблиці відповідностей, за якою досить просто побудувати схему. Із мікросхем шифраторів відомі, наприклад, К555ИВ3, КМ555ИАІ. Перетворювачі кодів Вони використовують спільну роботу дешифратора і шифратора. Дешифратор перетворює двійковий або двійково-десятковий код в унітарний, а шифратор – отриманий унітарний код в потрібний. Типовим прикладом використання такого перетворювача є схема перетворення коду в код керування семисегментним індикатором. Мультиплексор Це схема, що має n + 2 n входів і один вихід, де n – число адресних, а 2n – число інформаційних входів. Призначення мультиплексорів (від англ. multiplex – багатократний) – комутувати в бажаному порядку інформацію, що надходить з декількох вхідних шин на одну вихідну. За допомогою мультиплексора здійснюється тимчасове розділення інформації, що надходить по різних каналах. Його можна уподібнити безконтактному багатопозиційному перемикачу. Мультиплексори мають дві групи входів або один, частіше два, що взаємодоповнюються (інверсні) виходи. Одні входи інформаційні, а інші служать для керування. До них відносяться адресні і розв'язувальні. Адреса представляється в двійковому коді, причому кожній адресі відповідає інформаційний вхід, сигнал з якого (0 або 1) при даній адресі приходить на вихід. Таким чином, в мультиплексорі здійснюється 2n вхідних сигналів на один вихід. Розв'язувальний вхід керує одночасно всіма інформаційними входами незалежно від стану адресних входів. Заперечувальний сигнал на цьому вході блокує дію всього пристрою. Наявність розв'язувального входу розширює функціональні можливості мультиплексора, дозволяє синхронізувати його роботу з роботою інших вузлів. Цей вхід використовується також для нарощування розрядності мультиплексорів. У мультиплексорі, що виготовляється у вигляді окремих мікросхем, число інформаційних входів не перевищує 16. Більша кількість входів забезпечується шляхом нарощування. Нарощування можна виконувати об¢єднанням декількох мультиплексорів в пірамідоподібну (деревовидну) систему або послідовним з¢єднанням розв'язувальних входів і зовнішніх логічних елементів. Другий спосіб застосовується частіше за все, оскільки при пірамідоподібному нарощуванні більші витрати мікросхем і порівняно низька швидкодія через підсумовування затримок при послідовному проходженні сигналів за ступеням піраміди.
Для отримання 64–канального мультиплексора слід використовувати чотири БИС155КП1 і 4–вхідний елемент І–НІ, а керування входами Хід роботи 2.3.1 Від аналітичного завдання комбінаційної ф-ї (n=3) перейти до словесного та табличного, здійснити оптимізацію ф-ї двома методами: а) за допомогою діаграми Вейча-Карно; б) алгебраїчним методом на підставі законів алгебри Буля. Розробити комбінаційні схеми для вихідного та мінімізованого варіантів ф-ї на І, АБО, НІ. 2.3.2 Від матричного задання комбінаційної ф-ї (n=4) перейти до її аналітичного запису, виконати мінімізацію ф-ї, розробити комбінаційну схему в двох варіантах: а) на елементах І-НІ, АБО-НІ; б) на елементах І, АБО, НІ. Вибрати оптимальний варіант за кількістю елементів потрібних для реалізації схем. Реалізувати комбінаційну схему, що розроблена на попередній лабораторній роботі, користуючись універсальною монтажною платою; підключити схему до блока живлення, дослідити її функціонування, скласти таблицю відповідностей. Зміст звіту 2.4.1 Наприклад, задано комбінаційну ф-ю трьох аргументів F=
Х2
n=3 Мінімізація за допомогою діаграми Вейча-Карно F =
Розробляємо комбінаційну схему для мінімізованої ф-ї
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 151; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.78.203 (0.012 с.) |

 Ці форми відрізняються способом вказування зовнішніх і внутрішніх функцій розкладання. Наприклад, в ДНФ внутрішньою функцією (операцією, що виконується в першу чергу) є функція І, а зовнішньою – АБО, тобто, ДНФ є формою І – АБО.
Ці форми відрізняються способом вказування зовнішніх і внутрішніх функцій розкладання. Наприклад, в ДНФ внутрішньою функцією (операцією, що виконується в першу чергу) є функція І, а зовнішньою – АБО, тобто, ДНФ є формою І – АБО. –– форма І /АБО
–– форма І /АБО

 = –– форма І – НІ / І – НІ
= –– форма І – НІ / І – НІ –– форма АБО / І –НІ
–– форма АБО / І –НІ –– форма АБО – НІ/АБО
–– форма АБО – НІ/АБО .
.
 –– форма І / АБО –– НІ
–– форма І / АБО –– НІ –– форма І – НІ / І
–– форма І – НІ / І –– форма АБО / І
–– форма АБО / І


 –– форма АБО – НІ / АБО – НІ
–– форма АБО – НІ / АБО – НІ
 (2.1)
(2.1)






 необхідно виконувати інверсним чотирирозрядним унітарним кодом.
необхідно виконувати інверсним чотирирозрядним унітарним кодом.



 ;
; ;
;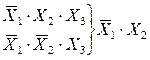 .
.



