

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Решение систем линейных уравнений. Прямые и итерационные методы.
Постановка задачи: Дана система линейных уравнений
A11*x1+A12*x2+A13*x3+A14*x4=B1
A21*x1+A22*x2+A23*x3+A24*x4=B2
A31*x1+A32*x2+A33*x3+A34*x4=B3
A41*x1+A42*x2+A43*x3+A44*x4=B4
· найти точное решение методом Гаусса
· найти приближённое решение методом простой итерации с точностью ε
· найти приближённое решение методом Зейделя с точностью ε
| Название метода
| Начальное приближение
| Итерационная формула
| Остановка процесса вычисления
| | Метод Гаусса
| Определитель матрицы не равен нулю
| Прямой ход – приведение матрицы к треугольному виду
Обратный ход – вычисление неизвестных, начиная с последнего уравнения
| Получение значений всех неизвестных
| | Метод простой итерации
| Проверка условия сходимости
|A11|>|A12|+|A13|+|A14|
|A22|>|A21|+|A23|+|A24|
|A33|>|A31|+|A32|+|A34|
|A44|>|A41|+|A42|+|A43|
Выбор начального приближения
x10=0 x20=0 x30=0 x40=0
| x1i+1=(B1-(A12*x2i+A13*x3i+A14*x4i))/ A11
x2i+1=(B2-(A21*x1i+A23*x3i+A24*x4i))/ A22
x3i+1=(B3-(A31*x1i+A32*x2i+A34*x4i))/ A33
x4i+1=(B4-(A41*x1i+A42*x2i+A43*x3i))/ A44
| |x1i+1-x1i|<ε
|x2i+1-x2i|<ε
|x3i+1-x3i|<ε
|x4i+1-x4i|<ε
| | Метод Зейделя
| Проверка условия сходимости
|A11|>|A12|+|A13|+|A14|
|A22|>|A21|+|A23|+|A24|
|A33|>|A31|+|A32|+|A34|
|A44|>|A41|+|A42|+|A43|
Выбор начального приближения
x10=0 x20=0 x30=0 x40=0
| x1i+1=(B1-(A12*x2i+A13*x3i+A14*x4i))/ A11
x2i+1=(B2-(A21*x1i+1+A23*x3i+A24*x4i))/ A22
x3i+1=(B3-(A31*x1i+1+A32*x2i+1+A34*x4i))/ A33
x4i+1=(B4-(A41*x1i+1+A42*x2i+1+A43*x3i+1))/ A44
| |x1i+1-x1i|<ε
|x2i+1-x2i|<ε
|x3i+1-x3i|<ε
|x4i+1-x4i|<ε
|
Метод Гаусса
Постановка задачи: Дана система линейных уравнений
A11*x1+A12*x2+A13*x3+A14*x4=B1
A21*x1+A22*x2+A23*x3+A24*x4=B2
A31*x1+A32*x2+A33*x3+A34*x4=B3
A41*x1+A42*x2+A43*x3+A44*x4=B4
найти точное решение методом Гаусса.
Запись системы линейных уравнений в матричном виде
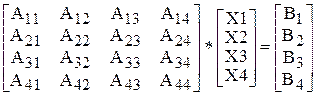

| Программа на языке CИ
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int main()
{ double a[4][4]={{5,1,1,1},{1,7,1,1},{1,1,6,1},{1,1,1,4}};
double b[4]={8,10,9,7};
double x[4];
int n,k,i,j;
n=4;
double c,s;
for(k=0;k<n-1;k++)
for(i=k+1;i<n;i++)
{
c=a[i][k]/a[k][k];
a[i][k]=0;
for(j=k+1;j<n;j++)
a[i][j]=a[i][j]-c*a[k][j];
b[i]=b[i]-c*b[k];
}
x[n-1]=b[n-1]/a[n-1][n-1];
for (i=n-1;i>=0;i--)
{
s=0;
for(j=i+1;j<n;j++)
{s=s+a[i][j]*x[j];
x[i]=(b[i]-s)/a[i][i];
}
}
cout<<"reshenie"<<endl;
for (i=0;i<n;i++)
cout<<x[i];
return 0;}
|

| Метод простой итерации.
Постановка задачи: Дана система линейных уравнений. Найти приближённое решение с точностью е.
Программа на языке CИ
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int main()
{ double
A[4][4]={{5,1,1,1},{1,7,1,1},{1,1,6,1},{1,1,1,4}};
double B[4]={8,10,9,7};
double X0[4],X1[4];
double eps,tochnost,max_tochnost,s;
int k,kmax,i,j;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout<<"Vvedite max chislo iter"<<endl;
cin>>kmax;
cout.precision(5);
cout.setf(ios::left);
for(i=0;i<4;i++) X0[i]=0;
k=0;
while(fabs(max_tochnost)>eps)
{
if(k>=kmax) break;
k=k+1;
cout<<setw(5)<<k;
max_tochnost=-100;
for(i=0;i<4;i++)
{s=0;
for(j=0;j<4;j++)
if(i!=j) s=s+A[i][j]*X0[j];
X1[i]=(B[i]-s)/A[i][i];
cout<<setw(10)<<X1[i];
tochnost=fabs(X1[i]-X0[i]);
if(tochnost>max_tochnost)
max_tochnost=tochnost;
}
cout<<endl;
for(i=0;i<4;i++) X0[i]=X1[i];
}
cout<<endl;
cout<<"Otvet"<<endl;
for(i=0;i<4;i++)
cout<<setw(10)<<X1[i];
cout<<endl;
cout<<"Chislo iter="<<k;
return 0;}
| 
| Метод Зейделя.
Постановка задачи: Дана система линейных уравнений. Найти приближённое решение с точностью е.
Программа на языке CИ
#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
int main()
{ double A[4][4]={{5,1,1,1},{1,7,1,1},{1,1,6,1},{1,1,1,4}};
double B[4]={8,10,9,7};
double X0[4],X1[4];
double eps,tochnost,max_tochnost,s;
int k,kmax,i,j;
cout<<"Vvedite tochnost"<<endl;
cin>>eps;
cout<<"Vvedite max chislo iter"<<endl;
cin>>kmax;
cout.precision(5);
cout.setf(ios::left);
for(i=0;i<4;i++) X0[i]=0;
k=0;
while(fabs(max_tochnost)>eps)
{
if(k>=kmax) break;
k=k+1;
cout<<setw(5)<<k;
max_tochnost=-100;
for(i=0;i<4;i++)
{s=0;
for(j=0;j<4;j++)
if(i!=j) s=s+A[i][j]*X0[j];
X1[i]=(B[i]-s)/A[i][i];
cout<<setw(10)<<X1[i];
tochnost=fabs(X1[i]-X0[i]);
if(tochnost>max_tochnost)
max_tochnost=tochnost;
X0[i]=X1[i];
}
cout<<endl;
}
cout<<endl;
cout<<"Otvet"<<endl;
for(i=0;i<4;i++)
cout<<setw(10)<<X1[i];
cout<<endl;
cout<<"Chislo iter="<<k;
return 0;}
| | | | | | |
Лабораторная работа №3
Аппроксимация и Интерполяции.
Постановка задачи: Дана таблица координат точек {xi,yi}
| x
| x0
| x1
| x2
| x3
| x4
| | y
| y0
| y1
| y2
| y3
| y4
| - Аппроксимировать точки полиномом 1 и 2 степени
- Интерполировать точки полиномом 1 и 2 степени
Метод наименьших квадратов
| Название метода
| Система для нахождения коэффициентов полинома
| Ответ
| | Метод наименьших квадратов
(аппроксимация)
| полином 1 степени
 полином 2 степени
полином 2 степени

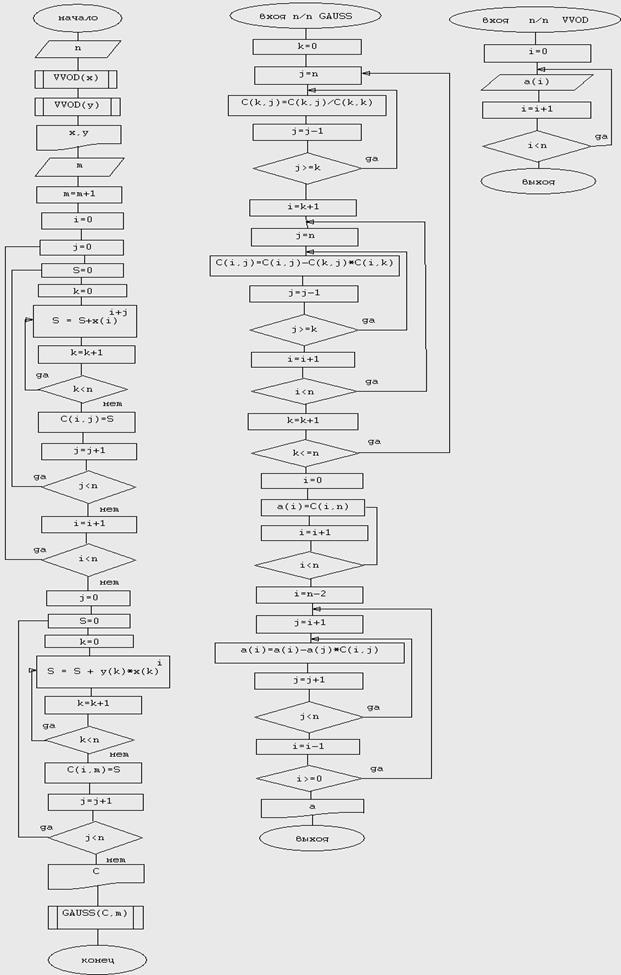
| P1(x)=a0+a1*x
P2(x)=a0+a1*x+a2*x2
| 
Программа на языке СИ
| #include <iostream.h>
#include <iomanip.h>
#include <math.h>
void gauss(double **c, int n)
{
int i,j;
cout.precision(3);
int k;
for (k=0; k<n; k++){
for (j=n; j>=k; j--)
c[k][j]/=c[k][k];
for (i=k+1; i<n; i++)
for (j=n; j>=k; j--)
c[i][j]-=c[k][j]*c[i][k];
}
double *a;
a=new double[n*sizeof(double)];
//Обратный ход
for (i=0; i<n; i++)
a[i]=c[i][n];
for (i=n-2; i>=0; i--)
for (j=i+1; j<n; j++)
a[i]-=a[j]*(c[i][j]);
//Печать результата
cout<<"Koeff\n";
for (j=0; j<n; j++)
cout<<"a"<<j<<"="<<a[j]<<endl;
delete[] a;
}
void vvod(double *a, int n)
{
for(int i=0;i<n;i++)
cin>>a[i];
}
int main()
{
int n,i,j;
cout<<"kol-vo tochek"<<endl;
cin>>n;
double **c;
double *x, *y;
x= new double[n];
cout<<"vvod x"<<endl;
vvod(x,n);
y= new double[n];
cout<<"vvod y"<<endl;
vvod(y,n);
| cout<<endl<<"prover'te koord tochek"<<endl;
for(i=0;i<n;i++)
cout<<"("<<x[i]<<","<<y[i]<<")"<<endl;
int m;
cout<<"stepen polinoma m"<<endl;
cin>>m;
m=m+1; //esli m=1, to yr-ya 2
c= new double *[m];
for(i=0;i<m;i++)
c[i]=new double[m];
int k;
double s;
for(i=0;i<m;i++)
for(j=0;j<m;j++){
s=0;
for(k=0;k<n;k++)
{
s=s+pow(x[k],(i+j));}
c[i][j]=s;}
for(i=0;i<m;i++){s=0;
for(k=0;k<n;k++)
{
s=s+y[k]*pow(x[k],i);}
c[i][m]=s;}
cout<<"Matritsa C+Y"<<endl;
for(i=0;i<m;i++)
{for(j=0;j<m+1;j++)
cout<<setw(5)<<c[i][j]<<" ";
cout<<endl;
}
cout<<endl;
gauss(c,m);
delete[] x;
delete[] y;
// for(i=0;i<n;i++)
// delete c[i];
delete[] c;
cin.get();
cin.get();
return 0;}
|
|



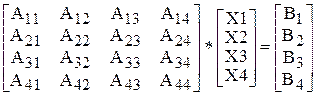



 полином 2 степени
полином 2 степени





