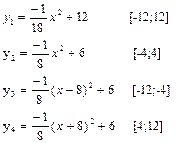Тема: «Решение уравнений графическим способом»

Задание 1. Составить таблицу для вычислений значений функций для всех х на интервале [-2;2] с шагом 0,2, при k=10. Построить совмещенные графики функций.

у₁=(х²-1) y₂=(х²-1)

	A	B	C	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V
	х	-2	-1,8	-1,6	-1,4	-1,2	-1	-0,8	-0,6	-0,4	-0,2		0,2	0,4	0,6	0,8		1,2	1,4	1,6	1,8
	у1
	у2
	у3

 

Задание 2. Найти корни нелинейного уравнения 0,5^х+1=(х-2)² графически на интервале [-4;4] с шагом 1 и уточнить один из методов проб с точностью до 0,01.

Для решения этой задачи данное уравнение преобразуем в систему уравнений. Для этого левую и правую часть уравнения приравниваем к нулю. Система будет иметь вид:

Для решения полученной системы уравнений графическим способом чертим графики обоих уравнений и абсцисса точки пересечения является корнем системы уравнений и следовательно данного нелинейного уравнения. Разберем все шаги:

1. Необходимо составить таблицу значений данной функции. Для заполнения ячеек значениями х введите первые два значения, выделите обе ячейки и протяните маркер заполнения вправо. Для заполнения ячеек значениями у введите формулу в первую ячейку и заполните маркером заполнения вправо. Таблица должна принять вид:

 

х	-4	-3	-2	-1
у						1,5	1,25	1,13	1,06
у1

 

2. Выделяем всю таблицу, в меню Вставка выбираем Диаграмма. Полученный график будет иметь вид:

 

 

3. Из графика видно, что первый корень находится в промежутке [0;1], второй - [3;4].

4. Уточним первый корень (диапазон [0;1]). Для этого в таблице меняем значения х таким образом: вместо значения х=-4 записываем 0, а вместо -3 записываем 0,1. Выделяем обе ячейки и проводим маркером заполнения вправо. Таблица примет вид:

 

х		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8
у		1,93	1,87	1,81	1,76	1,71	1,66	1,62	1,57
у1		3,61	3,24	2,89	2,56	2,25	1,96	1,69	1,44

 

При этом график автоматически примет вид:

Из нового графика видно, что корень находится в интервале [0,7; 0,8]. Уточняем корень таким же образом до сотых. Таблица примет вид:

 

х	0,7	0,71	0,72	0,73	0,74	0,75	0,76	0,77	0,78
у	1,62	1,61	1,61	1,60	1,60	1,59	1,59	1,59	1,58
у1	1,69	1,66	1,64	1,61	1,59	1,56	1,54	1,51	1,49

 

При этом график автоматически примет вид:

 

 

Получим ответ х=0,735

Таким же образом уточняем корень второго промежутка и находим х=3,06

Задание 3. Найти корни нелинейного уравнения х²+3=5-х² графически на интервале [-5;5] с шагом 0,5. Примечание: присвоить у₁=х²+3 и у₂=5-х², составить таблицу для вычислений значений, построить совмещенный график и найти точки пересечения двух графиков. Уточнить один из корней уравнения (точек пересечения) методом проб с точностью до 0,001.

 

Задание 4. Найти корень уравнения х³-6х²+9х+0,2=0 на интервале [-1;1] с шагом 0,2. Примечание: присвоить у=х³-6х²+9х+0,2, составить таблицу ля вычислений значений, построить график и найти точки пересечения графика с осью ОХ. Уточнить один из корней уравнения (точек пересечения) методом проб с точностью до 0,001.

 

Задание 5. Найти корень уравнения sinx+2cos²x-1=0 на интервале [3;4] с шагом 0,1. Уточнить один из корней уравнения (точек пересечения) методом проб с точностью до 0,001.

 

Задание 6. Составить таблицу для вычислений значений функций на интервале [-12;12] с шагом 1. Построить график следующих функций на одной координатной плоскости:

 

Задание 7. В одной координатной плоскости построить совмещенные графики функций с шагом 0,1.

у₁=е^х хÎ[-1;1] =ЕХР(х)

у₂=lg x хÎ[-0,1;1] =LOG10(x)

у₃=lg x+e^x хÎ[-0,1;1] =у₁+у₂

 

Задание 8. В одной координатной плоскости построить совмещенные графики функций для
хÎ[-4;4] с шагом 0,5.