
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение прямой по точке и вектору нормалиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой, заданной уравнением Ах + Ву + С = 0. Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0. Уравнение прямой, проходящей через две точки Пусть в пространстве заданы две точки M 1 (x 1, y 1, z 1) и M2 (x 2, y 2, z 2), тогда уравнение прямой, проходящей через эти точки:
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:
если х 1 ≠ х2 и х = х 1, если х 1 = х2. Дробь Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4). Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить Уравнение прямой по точке и направляющему вектору По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой. Определение. Каждый ненулевой вектор Ах + Ву + С = 0. Пример. Найти уравнение прямой с направляющим вектором Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям: 1 * A + (-1) * B = 0, т.е. А = В. Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0. при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение: х + у - 3 = 0 Уравнение прямой в отрезках Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим:
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу. Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1,
11.Угол между прямыми, расстояние от точки до прямой. Расстоянием от точки до прямой называется длина перпендикуляра, опущенного из точки на прямую. Если точка M0∈l, то ρ(M0,l)=0 (расстояние от точки M0 до прямой l) Для всякой точки M2/=M1 M0M2>M0M1
Oi→j→− прямоугольная система координат; M0(x0,y0);M1(x1,y1);
−−−−−−−→M0M1∣∣−→n, тогда −−−−−−−→M0M1·−→n=∣∣−−−−−−−→M0M11∣∣·∣−→n∣(±1)
−−−−−−−→M0M1(x1−x0,y1−y0);−→n(A,B);
−−−−−−−→M0M1·−→n=A(x1−x0)+B(y1−y0)=−(С+Ax0+By0)
Длина вектора −−→∣n∣=√A2+B2 Подставим все в выражение (1): −(С+Ax0+By0)=±ρ(M0,l)√A2+B2 Угол между двумя прямыми
Пусть даны 2 прямые d1,d2, причем они не параллельны и пересекаются в некоторой точке d1⋂d2=A.
0</(d1,d2)≤2π
Случай 1 Пусть даны 2 направляющих вектора для прямых d1,d2: a→(a1,a2)∣∣d1 и b→(b1,b2)∣∣d2, найдем tg(φ)=tg(/(d1,d2)) -? 1) d1⊥d2 тогда и только тогда, когда a→⊥b→⇔a→b→=0; a1b1+a2b2=0⇔φ=/(d1,d2)=±2π
tg(φ)=tg(/(a→,b→))=∣∣∣∣∣ a1 b1 a2 b2 ∣∣∣∣∣a1b1+a2b2
Случай 2 Пусть d1:A1x+B1y+C1=0
12.плоскость,ее уравнения. Определение. Плоскость - есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки. Общее уравнение плоскости Любую плоскость можно задать уравнением плоскости первой степени вида A x+ B y+ C z+ D= 0 где A, B и C не могут быть одновременно равны нулю.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 745; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.173.197 (0.006 с.) |

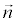 (3, -1).
(3, -1).

 = k называется угловым коэффициентом прямой.
= k называется угловым коэффициентом прямой.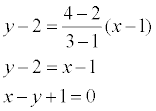

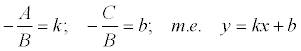 , то полученное уравнение называется уравнением прямой с угловым коэффициентом k.
, то полученное уравнение называется уравнением прямой с угловым коэффициентом k. (α1, α2), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой
(α1, α2), компоненты которого удовлетворяют условию А α1 + В α2 = 0 называется направляющим вектором прямой или
или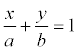 , где
, где
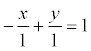 , а = -1, b = 1.
, а = -1, b = 1.


