
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В научной статистике широко используется показатель вариации, называемый дисперсией.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Дисперсия – это средний квадрат отклонений индивидуальных значений признака от средней арифметической.
Для не сгруппированных данных:
Для сгруппированных данных (дискретный ряд):
Для интервального ряда:
На дисперсии основаны практически все методы математической статистики. Дисперсия – наиболее широко применяемые показатели вариации. Объясняется это тем, что она входят в большинство теорем теории вероятности, служащих фундаментом математической статистики. Кроме того, дисперсия может быть разложена на составные элементы, позволяющие оценить влияние различных факторов, обуславливающих вариацию признака. Показатели вариации. Среднее квадратическое отклонение. Коэффициент вариации. Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака. Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Колебания отдельных значений характеризуют показатели вариации. Термин «вариация» произошел от лат. variatio – «изменение, колеблемость, различие». Под вариацией понимают количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую. Основными критериями разнообразия признака в статистической совокупности являются: квадратическое отклонение и коэффициент вариации. Определение перечисленных критериев разнообразия признака прежде всего осуществляется с учетом его значения у отдельных элементов статистической совокупности. Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако два ряда распределения, имеющих одинаковую среднюю арифметическую величину, могут значительно отличаться друг от друга по степени колеблемости (вариации) величины изучаемого признака. Если индивидуальные значения признака ряда мало отличаются друг от друга, то средняя арифметическая будет достаточно показательной характеристикой данной совокупности. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака, то средняя арифметическая будет ненадежной характеристикой этой совокупности и ее практическое применение будет ограничено. Значение показателей вариации заключается в следующем:
Для измерения вариации признака в рядах распределения применяются различные абсолютные и относительные показатели. В статистике чаще всего применяются следующие показатели (меры) вариации: среднее квадратическое отклонение и коэффициент вариации. Рассмотрим подробно каждый из перечисленных показателей вариации. Среднее квадратическое отклонение определяется как корень квадратный из среднего квадратов отклонений индивидуальных значений признака от средней арифметической и рассчитывается по следующим формулам:
для сгруппированных данных:
для интервального ряда:
Возведение индивидуальных отклонений в квадрат и последующее извлечение квадратного корня вызвано, как уже говорилось, тем, что суммирование отклонений в первой степени приводит к нулевому результату. Среднее квадратическое отклонение является общепринятым показателем вариации: при его определении принимаются в расчет все отклонения значений варьирующего признака от среднего. Проиллюстрируем расчет среднего квадратического отклонения для ранжированного и интервального вариационных рядов. Пример. Пусть испытываются шесть лампочек на продолжение горения. Результаты испытания представлены в табл. 6.3 (дискретный вариационный ряд). Таблица 6.3 Результаты испытаний лампочек
Рассчитаем среднюю арифметическую и среднее квадратическое отклонение:
Это означает, что в среднем продолжительность горения лампочки в изучаемой совокупности отклонялась от средней продолжительности в целом по совокупности на 14,3 часа. Пример. Рассчитаем среднее квадратическое отклонение срока обращения облигаций. Исходные данные для расчета и промежуточные вычисления представлены в табл. 6.4 (интервальный вариационный ряд). Рассчитаем среднюю арифметическую величину срока обращения акций и среднее квадратическое отклонение:
Таблица 6.4 Срок обращения облигаций
Среднее квадратическое отклонение – наиболее широко применяемые показатели вариации. Объясняется это тем, что оно входит в большинство теорем теории вероятности, служащих фундаментом математической статистики. Рассмотренные ранее показатели вариации. Так, например, среднее квадратическое отклонение урожайности пшеницы измеряется в центнерах. Так как среднеквадратическое отклонение – число именованное, то оно неудобно для сопоставления вариации различных признаков. Например, вычислив среднее квадратическое отклонение производительности работы и заработной платы рабочих, невозможно определить, вариация какого признака больше, т.к в первом случае она измеряется в единицах продукции (деталях), во втором – в рублях.
Принцип построения коэффициентов вариации таков
Чаще всего на практике употребляется квадратический коэффициент вариации. С помощью коэффициента вариации можно сравнивать размеры одного признака в нескольких совокупностях. Так, например, с помощью коэффициента вариации можно сравнивать вариацию срока службы станков на различных предприятиях, вариацию роста и веса населения в различных регионах страны. Пример. Рассмотрим коэффициенты вариации срока службы электролампочек, выпускаемых на трех заводах. Исходные данные представлены в табл. 6.5. Таблица 6.5 Срок службы электролампочек
Вычислим среднюю арифметическую срока горения лампочек:
Вычислим среднее квадратическое отклонение:
Вычислим коэффициент вариации для каждого завода и занесем данные в таблицу. Наиболее низкий коэффициент вариации у электролампочек, выпускаемых на заводе № 2, что свидетельствует о большой однородности его продукции (в данном случае, однородности качества электролампочек). Наиболее полную характеристику разнообразия признака в статистической совокупности дает среднее квадратическое отклонение В основе среднего квадратического отклонения лежит сопоставление каждой варианты
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.008 с.) |

 Дисперсия вычисляется по следующим формулам.
Дисперсия вычисляется по следующим формулам.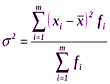
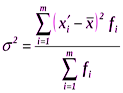
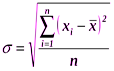 для не сгруппированных данных:
для не сгруппированных данных: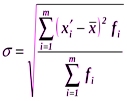

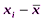
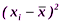
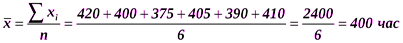
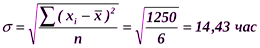
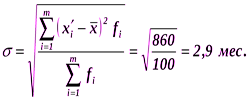
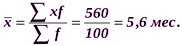 ;
;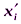
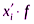
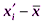
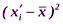
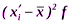
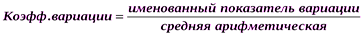 Для сравнения вариации разных признаков наиболее часто применяется показатель относительной колеблемости – коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности статистической совокупности. Статистическая совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному закону).
Для сравнения вариации разных признаков наиболее часто применяется показатель относительной колеблемости – коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности статистической совокупности. Статистическая совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному закону).
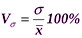
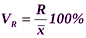
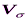 , %
, %
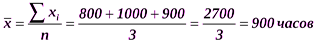 .
. .
.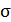 (сигма), которое является общей мерой отклонения вариант от своей средней величины. Среднее квадратическое отклонение часто называют также стандартным отклонением.
(сигма), которое является общей мерой отклонения вариант от своей средней величины. Среднее квадратическое отклонение часто называют также стандартным отклонением.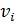 со средней арифметической
со средней арифметической 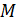 данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений
данной совокупности. Так как в совокупности всегда будут варианты как меньше, так и больше, чем она, то сумма отклонений  , имеющих знак "
, имеющих знак " 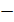 ", будет погашаться суммой отклонений, имеющих знак "
", будет погашаться суммой отклонений, имеющих знак " 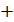 ", т.е. сумма всех отклонений
", т.е. сумма всех отклонений 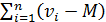 равна нулю. Для того, чтобы избежать влияния знаков разностей берут отклонения вариант от среднего арифметического в квадрате, т.е.
равна нулю. Для того, чтобы избежать влияния знаков разностей берут отклонения вариант от среднего арифметического в квадрате, т.е. 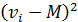 .
.


