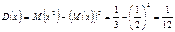Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства плотности распределенияСодержание книги
Поиск на нашем сайте
1) Плотность распределения – неотрицательная функция.
2) Несобственный интеграл от плотности распределения в пределах от - ¥ до ¥ равен единице.
Пример. Случайная величина подчинена закону распределения с плотностью:
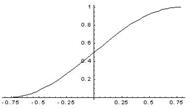
Требуется найти коэффициент а, построить график функции плотности распределения, определить вероятность того, что случайная величина попадет в интервал от 0 до Построим график плотности распределения:
Для нахождения коэффициента а воспользуемся свойством
Находим вероятность попадания случайной величины в заданный интервал.
Пример. Задана непрерывная случайная величина х своей функцией распределения f(x).
Требуется определить коэффициент А, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал Найдем коэффициент А.
Найдем функцию распределения:
1) На участке 2) На участке 3) На участке
Итого:
Построим график плотности распределения: f(x)
Построим график функции распределения: F(x)
Найдем вероятность попадания случайной величины в интервал
Математическое ожидание и дисперсия непрерывной случайной величины. Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно. С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Дисперсия случайной величины́ — мера разброса данной случайной величины, т. е. её отклонения от математического ожидания. Обозначается D[X]. В статистике часто употребляется обозначение
Определение. Пусть Х — случайная величина, определённая на некотором вероятностном пространстве. Тогда Математическое ожидание — понятие среднего значения случайной величины в теории вероятностей. Замечания. В силу линейности математического ожидания справедлива формула:
Дисперсия является вторым центральным моментом случайной величины;Дисперсия может быть бесконечной.
Свойства дисперсии 1.Дисперсия любой случайной величины неотрицательна: 2.Если дисперсия случайной величины конечна, то конечно и её математическое ожидание; 3.Если случайная величина равна константе, то её дисперсия равна нулю: D[a] = 0. Верно и обратное: если D[X] = 0, то X = M[X] п.н. 4.Пусть В частности: 1) 2) 3) 4) Пример Пусть случайная величина имеет стандартное непрерывное равномерное распределение на т. е. её плотность вероятности задана равенством
Тогда Тогда Математическое ожидание алгебраической суммы случайных величин и произведения независимых случайных величин. Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY) = M{X)M(Y). Свойство 4. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых: М (X + У) = М (X) + М (У). 14. Вероятность попадания значений НСВ на промежуток. Зная плотность распределения, можно вычислить вероятность того, что непрерывная случайная величина примет значение, принадлежащее заданному интервалу. Вычисление основано на следующей теореме. Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b: P (a < X < b)= a ∫ b [ f (x) dx ]. Нормальный закон распределения. Кривая плотности распределения, ее график и свойства. Семейство нормальных кривых.
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 320; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.7.53 (0.006 с.) |



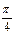 .
.
 .
.
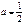
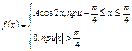
 .
.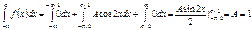
 :
: 
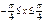 :
: 
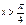 :
: 
 ;
; 

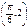 .
.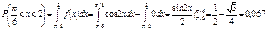 Ту же самую вероятность можно искать и другим способом:
Ту же самую вероятность можно искать и другим способом: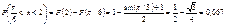
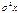 или
или 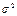 . Квадратный корень из дисперсии
. Квадратный корень из дисперсии  называется среднеквадратичным отклонением, стандартным отклонением или стандартным разбросом.
называется среднеквадратичным отклонением, стандартным отклонением или стандартным разбросом.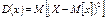 , где символ M обозначает математическое ожидание.
, где символ M обозначает математическое ожидание.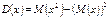

 — случайные величины, а
— случайные величины, а 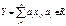 — их произвольная линейная комбинация. Тогда
— их произвольная линейная комбинация. Тогда 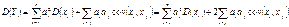 ,где — ковариация случайных величин
,где — ковариация случайных величин  .
. ,если
,если 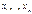 независимы;
независимы;


 .
. , и
, и  .
.