
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Несовместимые и совместимые события, полная группа событий. Алгебра событий: сумма событий, произведение событий, противоположное событие. Диаграмма Венна.Содержание книги
Поиск на нашем сайте
Понятие события в теории вероятностей, вероятность события, достоверное событие, невозможное событие. Классическая формула вычисления вероятности (схема «случаев»), статистическая вероятность, субъективная вероятность. Теория вероятностей – математическая наука, которая служит основой для анализа тех явлений окружающего мира, которым свойственна «изменчивость», и проявление которых не определяется однозначно условиями проводимых наблюдений. Событием в теории вероятностей называется произвольное подмножество множества элементарных исходов. Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные. Достоверным называется событие, которое обязательно произойдет в результате опыта (если будет осуществлена определенная совокупность условий S). Событие называется невозможным, если известно, что в результате опыта оно никогда не может произойти. Событие называется случайным, если в результате опыта оно может/не может произойти. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Если все события, которые могут произойти в результате данного опыта равновозможны и могут войти в одну группу – имеет место схема «случаев». (События наз. равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другие. События назыв. несовместными, если появление одного из них исключает появление другого.) Итак, вероятность события А определяется формулой: Р (А) = m / n, где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания. Наряду с классическим определением вероятности используют и другие определения, в частности статистическое и субъективное определение: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней (Относительной частотой события наз. отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.); субъективная вероятность – оценка наблюдателем, действующим лицом или иным индивидом возможности наступления определенного события на основании повторного опыта. Несовместимые и совместимые события, полная группа событий. Алгебра событий: сумма событий, произведение событий, противоположное событие. Диаграмма Венна. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. В противном случае события называются совместимыми, т.е. которые могут произойти одновременно. Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. (Теорема: Сумма вероятностей событий А1, А2, …, Аn, образующих полную группу, равна единице: Р (А1) + Р (А2) + …+ Р (Аn) = 1) Суммой двух событий А + В наз. событие, состоящее в том, что произошло или событие А или событие В, или они произошли одновременно. Произведением событий наз. событие, состоящее в том, что события А и В произошли одновременно. Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать
Функция распределения. Во всех рассмотренных выше случаях случайная величина определялась путем задания значений самой величины и вероятностей этих значений. Однако, такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, ее значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально. Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов? Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин. Пусть х – действительное число. Вероятность события, состоящего в том, что Х примет значение, меньшее х, т.е. Х < x, обозначим через F(x). Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.
Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения. Для дискретной случайной величины функция распределения имеет вид:
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х. Функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение хi. Плотность распределения Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси. Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема. Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов. После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины. Определение. Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением(может быть, конечного числа точек. Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу. Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b.
Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше. Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=a и x=b. Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:
Свойства дисперсии 1.Дисперсия любой случайной величины неотрицательна: 2.Если дисперсия случайной величины конечна, то конечно и её математическое ожидание; 3.Если случайная величина равна константе, то её дисперсия равна нулю: D[a] = 0. Верно и обратное: если D[X] = 0, то X = M[X] п.н. 4.Пусть В частности: 1) 2) 3) 4) Пример Пусть случайная величина имеет стандартное непрерывное равномерное распределение на т. е. её плотность вероятности задана равенством
Тогда Тогда Равномерное распределение Распределение вероятностей называют равномерным, есливсе значения кот лежат на некот интерв [a,b] и имеют постоянную плотность вероятности на этом отрезке.
Т.О. т.к. S=(b-a)*c=1, то с=1/(b-a) M(x)= M(x2)= D(x)= M(x2) - M2(x)=
D(x) зависит от длинны отрезка. Мода и её свойства. Мода — это просто наиболее часто встречающееся в определенной совокупности наблюдений значение переменной. При сгруппированных данных мода определяется как середина интервала группирования, содержащего наибольшее число значений наблюдаемой переменной. Модой Мо(Х) случайной величины Х называется ее наиболее вероятное значение(для которого вероятность pi или плотность вероятности достигает максимума). Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках,распределение называется полимодльным. Модальный интервал – интервал с наибольшей частотой. Графически моданаходится по гистограмме. достигает максимума). Если вероятность или плотность вероятности достигает максимума не в одной, а в нескольких точках,распределение называется полимодльным. Модальный интервал – интервал с наибольшей частотой. Графически моданаходится по гистограмме.
Статистическая совокупность. Генеральная совокупность. Выборка. Репрезентативность выборки. Таблица случайных чисел. Совокупность, состоящая из однородных элементов, имеющих качественную общность, будем называть статистической совокупностью. Элементы, из которых состоит данная совокупность, называют ее членами. Количество элементов в совокупности называют его объемом. Объем совокупности будем обозначать через N. Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных из генеральной совокупности объектов, отобранных для изучения. Генеральной совокупностью называют совокупность объектов, из которых производится выборка. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n =100.
Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Другими словами, выборка должна правильно представлять пропорции генеральной совокупности. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной). В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку. Ц.П.Т. Ляпунова Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины { Xi } имеют конечный третий момент. Тогда определена последовательность
то
Распределение Стьюдента Пусть Z – нормальная случайная величина, причём M(Z)=0,
Имеет распределение, которое называют t-распределением или распределением Стьюдента(псевдоним английского статистика В.Госсета), с k степенями свободы. Итак, отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределённой по закону «хи квадрат» с k степенями свободы, делённой на k, распределено по закону Стьюдента с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.
Понятие события в теории вероятностей, вероятность события, достоверное событие, невозможное событие. Классическая формула вычисления вероятности (схема «случаев»), статистическая вероятность, субъективная вероятность. Теория вероятностей – математическая наука, которая служит основой для анализа тех явлений окружающего мира, которым свойственна «изменчивость», и проявление которых не определяется однозначно условиями проводимых наблюдений. Событием в теории вероятностей называется произвольное подмножество множества элементарных исходов. Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные. Достоверным называется событие, которое обязательно произойдет в результате опыта (если будет осуществлена определенная совокупность условий S). Событие называется невозможным, если известно, что в результате опыта оно никогда не может произойти. Событие называется случайным, если в результате опыта оно может/не может произойти. Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Если все события, которые могут произойти в результате данного опыта равновозможны и могут войти в одну группу – имеет место схема «случаев». (События наз. равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другие. События назыв. несовместными, если появление одного из них исключает появление другого.) Итак, вероятность события А определяется формулой: Р (А) = m / n, где m – число элементарных исходов, благоприятствующих А; n – число всех возможных элементарных исходов испытания. Наряду с классическим определением вероятности используют и другие определения, в частности статистическое и субъективное определение: в качестве статистической вероятности события принимают относительную частоту или число, близкое к ней (Относительной частотой события наз. отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.); субъективная вероятность – оценка наблюдателем, действующим лицом или иным индивидом возможности наступления определенного события на основании повторного опыта. Несовместимые и совместимые события, полная группа событий. Алгебра событий: сумма событий, произведение событий, противоположное событие. Диаграмма Венна. События называют несовместными, если появление одного из них исключает появление других событий в одном и том же испытании. В противном случае события называются совместимыми, т.е. которые могут произойти одновременно. Несколько событий образуют полную группу, если в результате испытания появится хотя бы одно из них. Другими словами, появление хотя бы одного из событий полной группы есть достоверное событие. В частности, если события, образующие полную группу, попарно несовместны, то в результате испытания появится одно и только одно из этих событий. (Теорема: Сумма вероятностей событий А1, А2, …, Аn, образующих полную группу, равна единице: Р (А1) + Р (А2) + …+ Р (Аn) = 1) Суммой двух событий А + В наз. событие, состоящее в том, что произошло или событие А или событие В, или они произошли одновременно. Произведением событий наз. событие, состоящее в том, что события А и В произошли одновременно. Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать
|
|||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 1218; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.57.239 (0.008 с.) |

 . Диаграмма Венна – общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки и математики: теория множеств, теория вероятностей и др. Собственно «диаграмма Венна» показывает все возможные отношения м/у множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большое число множеств, но он смог это сделать только для четырех множеств, используя эллипсы:
. Диаграмма Венна – общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки и математики: теория множеств, теория вероятностей и др. Собственно «диаграмма Венна» показывает все возможные отношения м/у множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большое число множеств, но он смог это сделать только для четырех множеств, используя эллипсы:






 — случайные величины, а
— случайные величины, а 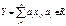 — их произвольная линейная комбинация. Тогда
— их произвольная линейная комбинация. Тогда 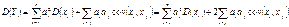 ,где — ковариация случайных величин
,где — ковариация случайных величин  .
. ,если
,если 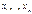 независимы;
независимы;


 .
. , и
, и  .
.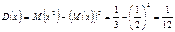

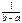
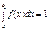 или
или  след.
след. 






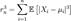 . Если предел
. Если предел (условие Ляпунова),
(условие Ляпунова), по распределению при
по распределению при 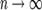 .
. (Z)=1, а V – независимая от Z величина, которая распределена по закону
(Z)=1, а V – независимая от Z величина, которая распределена по закону 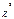 c k степенями свободы. Тогда величина
c k степенями свободы. Тогда величина Т=
Т= 



