
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Распределение выборочных средних. Центральная предельная теорема, стандартная ошибка средней.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Выборочная средняя Xв называют среднее арифметическое значение признака выборочной совокупности. Если все значения Х1, Х2,…,Хn признака выборки объёма n различны, то Xв=(Х1+Х2+…+Хn)/n Если же значения признака Х1, Х2,…, Хk имеют соответственно частоты n1, n2, …,nk, причём, n1 + n2 + … + nk = n,то Xв=(n1*Х1+ n2*Х2+…+ nk * Хn)/n Т.е. выборочная средняя есть средняя взвешенная значений признака с весами, равными соответствующим частотам. Центральная предельная теорема (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения. Классическая формулировка Ц.П.Т. Пусть
Обозначив символом
Ц.П.Т. Ляпунова Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины { Xi } имеют конечный третий момент. Тогда определена последовательность
то
Доверительные интервалы для средней при больших выборках. Поправка на конечность генеральной совокупности. Для построения доверит интервалов для параметров генеральных совокупностей могут быть реализованы два подхода,основанных на значении точного(при данном объеме выборки n) или асимптотического (при n→∞) распределения выборочных характеристик или некоторых функций от них. Первый подход-для построения интервальных оценок параметро для малых выборок, второй-для больших выборок. Теорема. Вероятность того,что отклонение выборочной средней(или доли) от генеральной средней(или доли) не превзойдет число ∆>0 (по абсолютной величине) равна: Доверительные интервалы для средней при малых выборках. t-распределение Стьюдента, степень свободы. Поправка на конечность генеральной совокупности. Задача построения доверительного интервала для генеральной средней может быть решена,если в генеральной совокупности рассматриваемый признак имеет нормальное распределение. Теорема. Если признак(случайная величина) Х имеет нормальный закон распределения с параметрами М(Х)=х0, Распределение Стьюдента Пусть Z – нормальная случайная величина, причём M(Z)=0,
Имеет распределение, которое называют t-распределением или распределением Стьюдента(псевдоним английского статистика В.Госсета), с k степенями свободы. Итак, отношение нормированной нормальной величины к квадратному корню из независимой случайной величины, распределённой по закону «хи квадрат» с k степенями свободы, делённой на k, распределено по закону Стьюдента с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.
|
||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 499; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.52.111 (0.006 с.) |

 есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ и σ2, соответственно. Пусть
есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ и σ2, соответственно. Пусть  . Тогда
. Тогда по распределению при
по распределению при  .
. выборочное среднее первых n величин, то есть
выборочное среднее первых n величин, то есть  , мы можем переписать результат центральной предельной теоремы в следующем виде:
, мы можем переписать результат центральной предельной теоремы в следующем виде: по распределению при
по распределению при  имеет распределение близкое к N (μ,σ2 / n).
имеет распределение близкое к N (μ,σ2 / n).  , получаем
, получаем  , где Φ(x) — функция распределения стандартного нормального распределения.
, где Φ(x) — функция распределения стандартного нормального распределения. 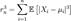 . Если предел
. Если предел (условие Ляпунова),
(условие Ляпунова), по распределению при
по распределению при 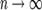 .
. , где
, где  .
.  ,где
,где 
 , т.е.
, т.е.  ,то выборочная средняя х пи любом n(а не только при n→∞) имеет нормальный закон распределения
,то выборочная средняя х пи любом n(а не только при n→∞) имеет нормальный закон распределения  .
. (Z)=1, а V – независимая от Z величина, которая распределена по закону
(Z)=1, а V – независимая от Z величина, которая распределена по закону 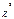 c k степенями свободы. Тогда величина
c k степенями свободы. Тогда величина Т=
Т= 



