
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выборочные числовые характеристики, формулы для их подсчета.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для выборки О: Средним арифметическим выборки Пусть О: Оценка если т.е. Т: Среднее арифметическое М* выборки В качестве оценки математического ожидания генеральной совокупности
Пример 3: Найти параметры распределения случайной величины Плотность вероятности для нормального закона распределения
неизвестные параметры — Так как
Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероятности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение. ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ Непрерывная случайная величина X, функция плотности которой задается выражением
называется случайной величиной, имеющей показательное, или экспоненциальное, распределение. Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению.
Графическое представление экспериментальных данных Дли повышения наглядности эмпирических распределений, используется их графическое представление. Наиболее распространенными способами графического представления являются гистограмма, полигон частот и полигон накопленных частот (кумулята). Гистограмма Гистограмма используется для графического представления распределений непрерывно варьирующих признаков и состоит из примыкающих друг к другу прямоугольников, как показано на рис. 2.1. Основание каждого прямоугольника равно ширине интервала группировки, а высота его такова, что площадь прямоугольника пропорциональна частоте (или частости) попадания в данный интервал. Если ряд безинтервальный, то ширина всех столбцов выбирается произвольной, но одинаковые. Таким образом, высоты прямоугольников должны быть пропорциональны величинам где ni — частота i -го интервала группировки; hi — ширина i -го интервала группировки. На графике гистограммы основание прямоугольников откладывается по оси абсцисс (x), а высота — по оси ординат (у) прямоугольной системы координат. Однако в тех случаях, когда ширина всех интервалов группировки одинакова, вид гистограммы не изменится, если по оси ординат откладывать не величины рi, а частоты интервалов ni.
Рис. 2.1. Гистограмма распределения результатов в предыдущем примере (когда ширина некоторых интервалов группировки неодинакова). В этом случае чтобы не нарушить принцип построения гистограммы (площади прямоугольников пропорциональны частотам интервалов), по оси ординат уже нельзя откладывать частоты, а надо – высоты прямоугольников (которые должны быть пропорциональны отношениям Полигон частот Другим распространенным способом графического представления является полигон частот. Полигон частот образуется ломаной линией, соединяющей точки, соответствующие срединным значениям интервалов группировки и частотам этих интервалов, срединные значения откладываются по оси х, а частоты – по оси у. Из сравнения двух рассмотренных способов графического представления эмпирических распределений следует, что для получения полигона частот из построенной гистограммы нужно середины вершин прямоугольников, образующих гистограмму, соединить отрезками прямых. Пример полигона частот представлен на рис. 2.2. Рис. 2.2. Полигон частот Полигон частот используется для представления распределений как непрерывных, так и дискретных признаков. В случае непрерывного распределения полигон частот является более предпочтительным способом графического представления, чем гистограмма, если график эмпирического распределения описывается плавной зависимостью. 21. Гипо́теза (др.-греч. ὑπόθεσις — предположение; от ὑπό — снизу, под + θέσις — тезис) — предположение или догадка; утверждение, предполагающее доказательство, в отличие отаксиом , постулатов, не требующих доказательств. Гипотеза считается научной, если она удовлетворяет критерию Поппера, т.е. потенциально может быть проверена критическим экспериментом, а так же если она соответствует другим критериям, отличающим науку от не науки.Статистическая гипотеза – это предположение о свойствах случайных величин или событий, которое мы хотим проверить по имеющимся данным. Примеры статистических гипотез в педагогических исследованиях: Гипотеза 1. Успеваемость класса стохастически (вероятностно) зависит от уровня обучаемости учащихся. Гипотеза 2. Усвоение начального курса математики не имеет существенных различий у учащихся, начавших обучение с 6 или 7 лет. Гипотеза 3. Проблемное обучение в первом классе эффективнее по сравнению с традиционной методикой обучения в отношении общего развития учащихся. Пример 1. Процесс производства некоторого медицинского препарата весьма сложен. Несущественные на первый взгляд отклонения от технологии вызывают появление высокотоксичной побочной примеси. Токсичность этой примеси может оказаться столь высокой, что даже такое ее количество, которое не может быть обнаружено при обычном химическом анализе, может оказаться опасным для человека, принимающего это лекарство. В результате, прежде чем выпускать в продажу вновь произведенную партию, ее подвергают исследованию на токсичность биологическими методами. Малые дозы лекарства вводятся некоторому количеству подопытных животных, например, мышей, и результат регистрируют. Если лекарство токсично, то все или почти все животные гибнут. В противном случае норма выживших велика. Исследование лекарства может привести к одному из возможных способов действия: выпустить партию в продажу (а1), вернуть партию поставщику для доработки или, может быть, для уничтожения (а2). Ошибки двух видов, связанные с действиями а1 и а2 совершенно различны, различна и важность избежания их. Сначала рассмотрим случай, когда применяется действие а1, в то время когда предпочтительнее а2. Лекарство опасно для пациента, в то время как оно признано безопасным. Ошибка этого вида может вызвать смерть пациентов, употребляющих этот препарат. Это ошибка первого рода, так как нам важнее ее избежать. Рассмотрим случай когда предпринимается действие а2, в то время когда а1 является более предпочтительным. Это означает, что вследствие неточностей в проведении эксперимента партия нетоксичного лекарства классифицировалась как опасная. Последствия ошибки могут выражаться в финансовом убытке и в увеличении стоимости лекарства. Однако случайное отвержение совершенно безопасного лекарства, очевидно, менее нежелательно, чем, пусть даже изредка происходящие гибели пациентов. Отвержение нетоксичной партии лекарства – ошибка второго рода. Допустимая вероятность ошибки первого рода (Ркр) может быть равна 5% или 1% (0.05 или 0.01). 22. Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных. Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергается статистическая гипотеза. · 23.классификация гипотез · простая – указано одно обстоятельство, при наличии или отсутствии которого действует юридическая норма; · сложная – наличие в гипотезе одновременно двух или более обстоятельств, в совокупности обусловливающих действие нормы; · альтернативная – указано несколько вариантов обстоятельств (альтернативных), при которых возможно действие нормы. В этом случае при наступлении одного из них норма является действующей;
Параметрической гипотезой называется гипотеза о значениях параметров распределения или о сравнительной величине параметров двух распределений. Примером параметрической статистической гипотезы является гипотеза о равенстве математических ожиданий двух нормальных совокупностей. Непараметрическими гипотезами называются гипотезы о виде распределенияслучайной величины. Нулевой, основной или проверяемой гипотезой называется первоначально выдвинутая гипотеза, которая обозначается Н0.
24. Статистическая гипотеза представляет собой некоторое предположение о законе распределения случайной величины или о параметрах этого закона, формулируемое на основе выборки [3, 5, 11]. Примерами статистических гипотез являются предположения: генеральная совокупность распределена по экспоненциальному закону; математические ожидания двух экспоненциально распределенных выборок равны друг другу. В первой из них высказано предположение о виде закона распределения, а во второй – о параметрах двух распределений. Гипотезы, в основе которых нет никаких допущений о конкретном виде закона распределения, называют непараметрическими, в противном случае – параметрическими. Гипотезу, утверждающую, что различие между сравниваемыми характеристиками отсутствует, а наблюдаемые отклонения объясняются лишь случайными колебаниями в выборках, на основании которых производится сравнение, называют нулевой (основной) гипотезой и обозначают Н 0. Наряду с основной гипотезой рассматривают и альтернативную (конкурирующую, противоречащую) ей гипотезу Н 1. И если нулевая гипотеза будет отвергнута, то будет иметь место альтернативная гипотеза. Различают простые и сложные гипотезы. Гипотезуназывают простой, если она однозначно характеризует параметр распределения случайной величины. Например, если является параметром экспоненциального распределения, то гипотеза Н 0 о равенстве = 10–простая гипотеза. Сложной называют гипотезу, которая состоит из конечного или бесконечного множества простых гипотез. Сложная гипотеза Н 0 о неравенстве > 10 состоит из бесконечного множества простых гипотез Н 0 о равенстве =bi, где bi – любое число, большее 10. Гипотеза Н 0 о том, что математическое ожидание нормального распределения равно двум при неизвестной дисперсии, тоже является сложной. Сложной гипотезой будет предположение о распределении случайной величины Х по нормальному закону, если не фиксируются конкретные значения математического ожидания и дисперсии. Проверка гипотезы основывается на вычислении некоторой случайной величины – критерия, точное или приближенное распределение которого известно. Обозначим эту величину через z, ее значение является функцией от элементов выборки z = z (x1, x2, …, xn). Процедура проверки гипотезы предписывает каждому значению критерия одно из двух решений – принять или отвергнуть гипотезу. Тем самым все выборочное пространство и соответственно множество значений критерия делятся на два непересекающихся подмножества S 0 и S 1. Если значение критерия z попадает в область S 0, то гипотеза принимается, а если в область S 1, – гипотеза отклоняется. Множество S 0называется областью принятия гипотезы или областью допустимых значений, а множество S 1 – областью отклонения гипотезы или критической областью. Выбор одной области однозначно определяет и другую область. Принятие или отклонение гипотезы Н 0 по случайной выборке соответствует истине с некоторой вероятностью и, соответственно, возможны два рода ошибок. Ошибка первого рода возникает с вероятностью тогда, когда отвергается верная гипотеза Н 0 и принимается конкурирующая гипотеза Н 1. Ошибка второго рода возникает с вероятностью в том случае, когда принимается неверная гипотеза Н 0, в то время как справедлива конкурирующая гипотеза Н 1. Доверительная вероятность – это вероятность не совершить ошибку первого рода и принять верную гипотезу Н 0. Вероятность отвергнуть ложную гипотезу Н 0 называется мощностью критерия. Следовательно, при проверке гипотезы возможны четыре варианта исходов, табл. 3.1. Таблица 3.1.
Например, рассмотрим случай, когда некоторая несмещенная оценка параметра вычислена по выборке объема n, и эта оценка имеет плотность распределения f (), рис. 3.1.
Рис. 3.1. Области и отклонения гипотезы Предположим, что истинное значение оцениваемого параметра равно Т. Если рассматривать гипотезу Н 0 о равенстве = Т, то насколько велико должно быть различие между и Т, чтобы эту гипотезу отвергнуть. Ответить на данный вопрос можно в статистическом смысле, рассматривая вероятность достижения некоторой заданной разности между и Т на основе выборочного распределения параметра . Целесообразно полагать одинаковыми значения вероятности выхода параметра за нижний и верхний пределы интервала. Такое допущение во многих случаях позволяет минимизировать доверительный интервал, т.е. повысить мощность критерия проверки. Суммарная вероятность того, что параметр выйдет за пределы интервала с границами 1– /2 и /2, составляет величину . Эту величину следует выбрать настолько малой, чтобы выход за пределы интервала был маловероятен. Если оценка параметра попала в заданный интервал, то в таком случае нет оснований подвергать сомнению проверяемую гипотезу, следовательно, гипотезу равенства = Т можно принять. Но если после получения выборки окажется, что оценка выходит за установленные пределы, то в этом случае есть серьезные основания отвергнуть гипотезу Н 0. Отсюда следует, что вероятность допустить ошибку первого рода равна (равна уровню значимости критерия). Если предположить, например, что истинное значение параметра в действительности равно Т + d, то согласно гипотезе Н 0 о равенстве = Т – вероятность того, что оценка параметра попадет в область принятия гипотезы, составит , рис. 3.2.
При заданном объеме выборки вероятность совершения ошибки первого рода можно уменьшить, снижая уровень значимости . Однако при этом увеличивается вероятность ошибки второго рода (снижается мощность критерия). Аналогичные рассуждения можно провести для случая, когда истинное значение параметра равно Т – d. Единственный способ уменьшить обе вероятности состоит в увеличении объема выборки (плотность распределения оценки параметра при этом становится более "узкой"). При выборе критической области руководствуются правилом Неймана – Пирсона: следует так выбирать критическую область, чтобы вероятность была мала, если гипотеза верна, и велика в противном случае. Однако выбор конкретного значения относительно произволен. Употребительные значения лежат в пределах от 0,001 до 0,2. В целях упрощения ручных расчетов составлены таблицы интервалов с границами 1– /2 и /2 для типовых значений и различных способов построения критерия. При выборе уровня значимости необходимо учитывать мощность критерия при альтернативной гипотезе. Иногда большая мощность критерия оказывается существеннее малого уровня значимости, и его значение выбирают относительно большим, например 0,2. Такой выбор оправдан, если последствия ошибок второго рода более существенны, чем ошибок первого рода. Например, если отвергнуто правильное решение "продолжить работу пользователей с текущими паролями", то ошибка первого рода приведет к некоторой задержке в нормальном функционировании системы, связанной со сменой паролей. Если же принято решения не менять пароли, несмотря на опасность несанкционированного доступа посторонних лиц к информации, то эта ошибка повлечет более серьезные последствия. В зависимости от сущности проверяемой гипотезы и используемых мер расхождения оценки характеристики от ее теоретического значения применяют различные критерии. К числу наиболее часто применяемых критериев для проверки гипотез о законах распределения относят критерии хи-квадрат Пирсона, Колмогорова, Мизеса, Вилкоксона, о значениях параметров – критерии Фишера, Стьюдента. 25. КРИТИЧЕСКАЯ ОБЛАСТЬ - часть выборочного пространства такая, что попадание в нее наблюденного значения случайной величины, с распределением к-рой связана проверяемая гипотеза, влечет отказ от этой гипотезы
Критическими точками (границами) k кр называют точки, отделяющие критическую область от области принятия гипотезы. 26. Случайная погрешность измерения образуется под влиянием большого числа факторов, сопутствующих процессу измерения. В каждой конкретной ситуации работает свой механизм образования погрешности. Поэтому естественно предположить, что каждой ситуации должен соответствовать свой тип распределения погрешности. Однако во многих случаях имеются возможности еще до проведения измерений сделать некоторые предположения о форме функции распределения, так что после проведения измерений остается только определить значения некоторых параметров, входящих в выражение для предполагаемой функции распределения. Случайная погрешность характеризует неопределенность наших знаний об истинном значении измеряемой величины, полученных в результате проведенных наблюдений. Согласно К. Шеннону мерой неопределенности ситуации, описываемой случайной величиной X, является энтропия [4]
Для выявления вида наиболее вероятных распределений рассмотрим несколько наиболее типичных случаев [3]. 1. В классе распределений результатов наблюдений Искомая плотность распределения результатов наблюдений описывается выражением
Значения дифференциальной функции распределения равномерной распределенной случайной погрешности постоянны в интервале [- а; + а ], а вне этого интервала равны нулю (рис.6).
Определим числовые характеристики равномерного распределения. Математическое ожидание случайной погрешности находим по формуле (10):
Дисперсию случайной равномерно распределенной погрешности можно найти по формуле (18):
В силу симметрии распределения относительно математического ожидания коэффициент асимметрии должен равняться нулю:
Для определения эксцесса найдем вначале четвертый момент случайной погрешности:
В заключение найдем веро-ятность попадания случайной погрешности в заданный интервал [
2. В классе распределений результатов наблюдений
Решение этой задачи также находится методом множителей Лагранжа. Искомая плотность распределения результатов наблюдений описывается выражением
Учитывая, что при полном исключении систематических погрешностей
Распределение, описываемое уравнениями (25) и (26), называется нормальным или распределением Гаусса. На рис.8 изображены кривые нормального распределения случайных погрешностей для различных значений среднеквадратического отклонения
Из рисунка видно, что по мере увеличения среднеквадратического отклонения распределение все более и более расплывается, вероятность появления больших значений погрешностей возрастает, а вероятность меньших погрешностей сокращается, т.е. увеличивается рассеивание результатов наблюдений. Вычислим вероятность попадания результата наблюдения в некоторый заданный интервал
Заменим переменные:
Интегралы, стоящие в квадратных скобках, не выражаются в элементарных функциях, поэтому их вычисляют с помощью так называемого нормированного нормального распределения с дифференциальной функцией
Широкое распространение нормального распределения погрешностей в практике измерений объясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем, в разработке которой принимали участие многие крупнейшие математики - Муавр, Лаплас, Гаусс, Чебышев и Ляпунов. Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко в нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных. 3. Предположим, что результаты наблюдений распределены нормально, но их среднеквадратическое отклонение является величиной случайной, изменяющейся от опыта к опыту. Такое предположение более осторожное, чем предположение о неизменности
где Дифференциальная функция распределения случайных погрешностей получается подстановкой
Асимметрия распределения равна нулю, поскольку распределение симметрично относительно нуля, а эксцесс в соответствии с формулой (22) составляет
Таким образом, по сравнению с нормальным распределением (Ех = 0) равномерное распределение является более плосковершинным (Ех = -1.2), а распределение Лапласа - более островершинным (Ех = 3).
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 571; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.85.233 (0.011 с.) |

 СВ
СВ  и для статистического ряда определяются следующие числовые характеристики.
и для статистического ряда определяются следующие числовые характеристики. называется
называется  средним арифметическим статистического ряда (36.1):
средним арифметическим статистического ряда (36.1):  Дисперсией выборки
Дисперсией выборки  называется
называется  дисперсией статистического ряда (36.1) —
дисперсией статистического ряда (36.1) —  Средним квадратическим отклонением называется
Средним квадратическим отклонением называется 
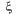 — случайная величина с функцией распределения
— случайная величина с функцией распределения  где
где  — неизвестный параметр распределения, т.е. неизвестная числовая характеристика СВ
— неизвестный параметр распределения, т.е. неизвестная числовая характеристика СВ  Например,
Например,  имеет нормальное распределение с неизвестным параметром
имеет нормальное распределение с неизвестным параметром  Рассмотрим
Рассмотрим  выборок
выборок  этой СВ
этой СВ  Обозначим через
Обозначим через  оценку величины 9, ее можно представить как случайную величину, зависящую от
оценку величины 9, ее можно представить как случайную величину, зависящую от 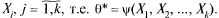 Чтобы выбрать в некотором смысле лучшую оценку
Чтобы выбрать в некотором смысле лучшую оценку  рассматриваются свойства оценок: несмещенность, состоятельность, эффективность.
рассматриваются свойства оценок: несмещенность, состоятельность, эффективность. параметра
параметра  называется несмещенной, если ее математическое ожидание
называется несмещенной, если ее математическое ожидание  состоятельной,
состоятельной, по вероятности сходится к
по вероятности сходится к  при
при 
 Несмещенная оценканазывается
Несмещенная оценканазывается  эффективной, если ее дисперсия
эффективной, если ее дисперсия  — наименьшая среди всех дисперсий, вычисляемых для оценок
— наименьшая среди всех дисперсий, вычисляемых для оценок  по выборкам одинакового объема.
по выборкам одинакового объема. случайной величины
случайной величины  имеющей математическое ожидание
имеющей математическое ожидание  и дисперсию
и дисперсию  является несмещенной и состоятельной оценкой математического ожидания. В случае нормального распределения СВ
является несмещенной и состоятельной оценкой математического ожидания. В случае нормального распределения СВ  эта оценка является эффективной. Доказательство в [7. С. 505].
эта оценка является эффективной. Доказательство в [7. С. 505]. берется среднее арифметическое М* выборки. Выборочная дисперсия D* является смещенной состоятельной оценкой дисперсии, поэтому в качестве несмещенной состоятельной оценки дисперсии генеральной совокупности используется исправленная выборочная дисперсия
берется среднее арифметическое М* выборки. Выборочная дисперсия D* является смещенной состоятельной оценкой дисперсии, поэтому в качестве несмещенной состоятельной оценки дисперсии генеральной совокупности используется исправленная выборочная дисперсия (
( — объем выборки), S— исправленное среднее квадратическое отклонение. Если объем выборки достаточно большой
— объем выборки), S— исправленное среднее квадратическое отклонение. Если объем выборки достаточно большой  то
то  и в качестве оценки генеральной дисперсии берется D*.
и в качестве оценки генеральной дисперсии берется D*. в примере 2 разд. 36.1, если
в примере 2 разд. 36.1, если  имеет нормальный закон распределения.
имеет нормальный закон распределения.


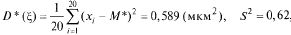


 Равномерное рапределение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [ а, в ], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:
Равномерное рапределение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [ а, в ], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:
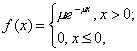

 , (2.6)
, (2.6)
 ).
).


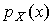 . Можно предположить, что любой процесс измерения формируется таким образом, что неопределенность результата наблюдений оказывается наибольшей в некоторых пределах, определяемых допускаемыми значениями погрешности. Поэтому наиболее вероятными должны быть такие распределения
. Можно предположить, что любой процесс измерения формируется таким образом, что неопределенность результата наблюдений оказывается наибольшей в некоторых пределах, определяемых допускаемыми значениями погрешности. Поэтому наиболее вероятными должны быть такие распределения  при наличии ограничивающих условий:
при наличии ограничивающих условий: ,
,  ,
,  ,
, - математическое ожидание результатов наблюдений. Решение поставленной задачи находится методом множителей Лагранжа.
- математическое ожидание результатов наблюдений. Решение поставленной задачи находится методом множителей Лагранжа.







 ], равный заштрихованной площади на рис.7
], равный заштрихованной площади на рис.7 

 , найдем такое, которое обращает в максимум энтропию
, найдем такое, которое обращает в максимум энтропию  при наличии ограничений:
при наличии ограничений: ,
,  ,
,  .
.
 - математическое ожидание и
- математическое ожидание и  - среднеквадратическое отклонение результатов наблюдений.
- среднеквадратическое отклонение результатов наблюдений. и
и  , для дифференциальной функции распределения случайной погрешности можно записать уравнение
, для дифференциальной функции распределения случайной погрешности можно записать уравнение
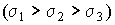 .
.
 :
:




 находят как
находят как


 и
и  в выражение (30):
в выражение (30):




