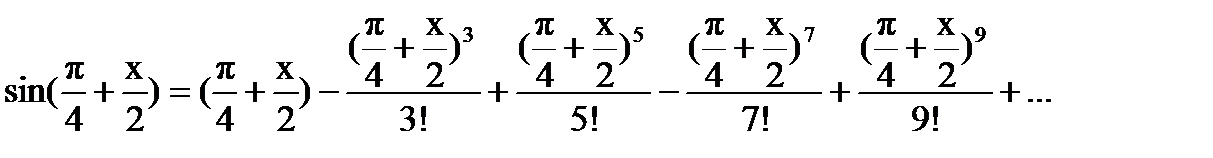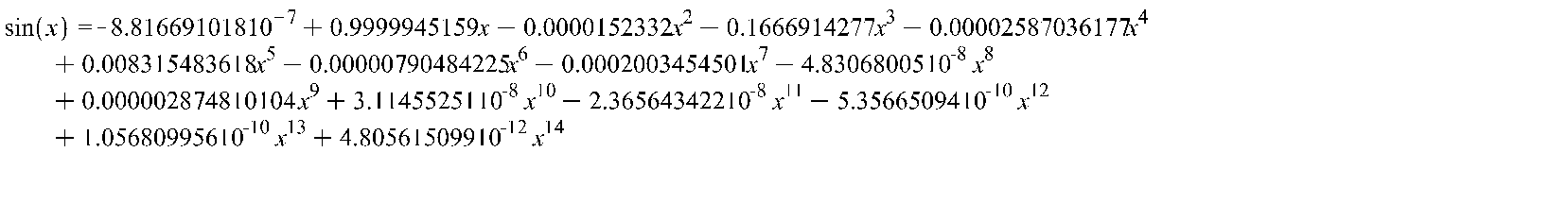Разложение функции синуса в ряд
Похожие статьи вашей тематики
Первое, что необходимо сделать при вычислении какой-либо функции по ее разложению в ряд, это уменьшить, если возможно, диапазон значений аргумента, для которых требуется это вычисление. Это может значительно уменьшить ошибку округления. «Математическое» определение синуса через его разложение в степенной ряд пригодно для всех значений аргумента, но при этом подразумевается, что вычисление синуса необходимо производить с бесконечно большим количеством значащих цифр. На практике при вычислениях с помощью ЭВМ степенной ряд для синуса становится совершенно бесполезным при больших значениях аргументах и дает совершенно бессмысленные результаты.
В случае синуса задача решается весьма просто:
 , ,
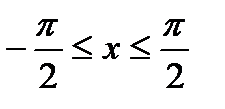
Таким образом, отнимая некоторое число, кратное 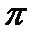 , мы сводим задачу нахождения синуса произвольного угла к задаче нахождения угла, лежащего между - , мы сводим задачу нахождения синуса произвольного угла к задаче нахождения угла, лежащего между - 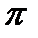 /2 и /2 и 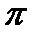 /2. /2.
На практике уменьшение аргумента не производится последовательным вычитанием. Вместо этого первоначальный угол делится на 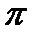 , причем деление организовано так, что частное получается целым. Остаток от деления будет определять собой некоторый угол, заключенный между 0 и , причем деление организовано так, что частное получается целым. Остаток от деления будет определять собой некоторый угол, заключенный между 0 и 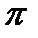 . Если остаток больше . Если остаток больше  /2, то еще одно вычитание дает угол между - /2, то еще одно вычитание дает угол между - 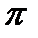 /2 и /2 и 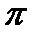 /2. Целое частное от деления исходного угла на /2. Целое частное от деления исходного угла на 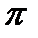 используется для того, чтобы определить, следует ли изменить знак окончательного результата (при нечетном частном). используется для того, чтобы определить, следует ли изменить знак окончательного результата (при нечетном частном).
Практическая часть
Алгоритм расчета функции синуса
В данной работе используется арифметика c фиксированной запятой, следовательно, требуется, чтобы все числа были представлены по абсолютному значению меньше единицы.
Для преставления функции синуса воспользуемся формулами приведения и двойного угла:
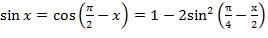 (1) (1)
для случая, когда аргумент лежит в интервале 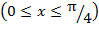 и и
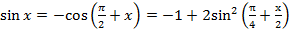 (2) (2)
для случая, когда аргумент лежит в интервале  . .
Рассмотрение двух случаев обусловлено тем, что невозможно использовать лишь одно соотношение (1), так как при расчетах будут возникать числа большие единицы.
В итоговых формулах расчета функции синуса (1) и (2) присутствует умножение на 2, которое будет заменено на сложение величины самой с собой.
Таким образом, число, поступающее на вход нашей машины, не будет превышать единицы по модулю, так как максимально возможный аргумент равен 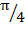 , либо , либо 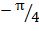 . .
Для представления формул (1) и (2) в виде общего ряда используем стандартный ряд Тейлора для синуса в диапазоне 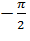 ≤ x ≤ ≤ x ≤  : :
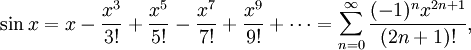
Для аргумента синуса равного 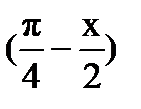 разложение в ряд Тейлора будет иметь следующий вид: разложение в ряд Тейлора будет иметь следующий вид:
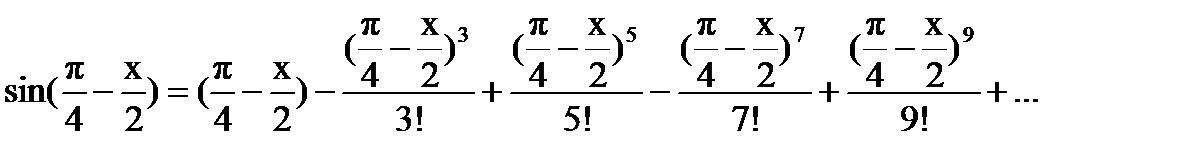
Далее, общий ряд для вычисления функции sin(x) по формуле (1):
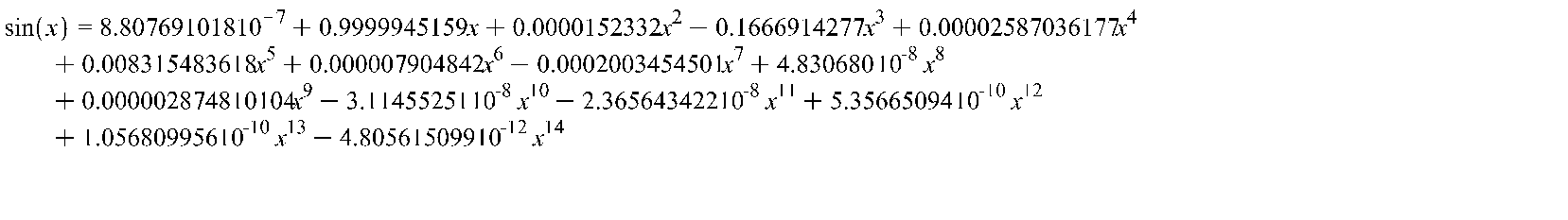
(3)
Разложение в ряд Тейлора для аргумента синуса, равного 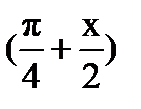 , будет иметь следующий вид: , будет иметь следующий вид:
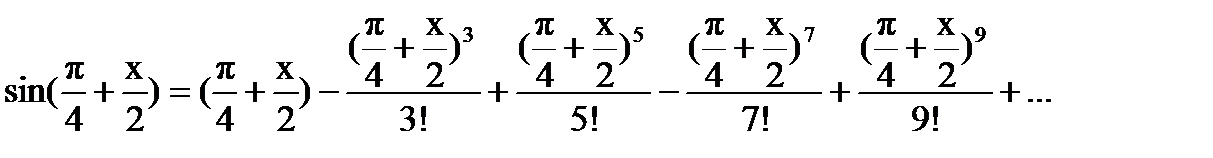
И общий ряд для вычисления sin(x) по формуле (2):
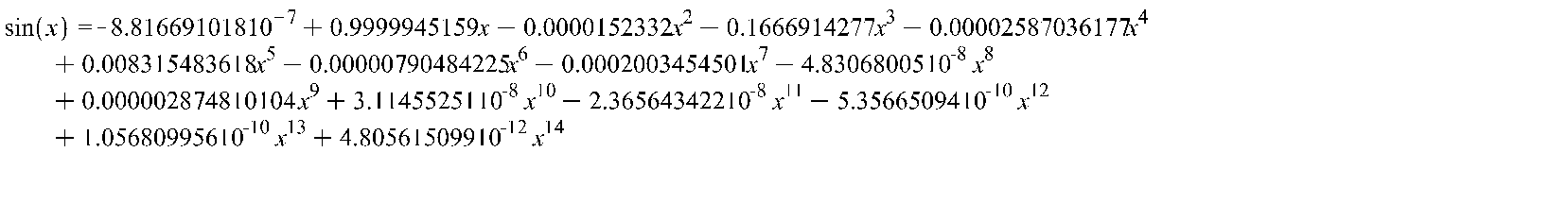
(4)
Будем рассматривать два случая:
1. В вычислительной машине реализована функция умножения. Алгоритм вычисления показан на Схеме 2.
2. В вычислительной машине не реализована функция умножения. При этом алгоритм процедуры умножения реализован отдельно и показан на Схеме 1. Алгоритм вычисления показан на Схеме 3.
| Сдвиг res на 1 разряд вправо
| | Сдвиг res на 1 разряд вправо
| | Схема 1. Блок-схема процедуры умножения
|
| Схема 2. Функция умножения в вычислительной машине реализована
| | Схема 2. Функция умножения в вычислительной машине реализована
| | Схема 3. Функция умножения в вычислительной машине не реализована
|
Оценка погрешностей
|



 ,
,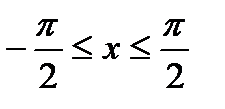
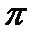 , мы сводим задачу нахождения синуса произвольного угла к задаче нахождения угла, лежащего между -
, мы сводим задачу нахождения синуса произвольного угла к задаче нахождения угла, лежащего между - 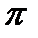 /2 и
/2 и 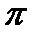 /2.
/2.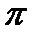 , причем деление организовано так, что частное получается целым. Остаток от деления будет определять собой некоторый угол, заключенный между 0 и
, причем деление организовано так, что частное получается целым. Остаток от деления будет определять собой некоторый угол, заключенный между 0 и 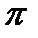 . Если остаток больше
. Если остаток больше  /2, то еще одно вычитание дает угол между -
/2, то еще одно вычитание дает угол между - 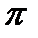 используется для того, чтобы определить, следует ли изменить знак окончательного результата (при нечетном частном).
используется для того, чтобы определить, следует ли изменить знак окончательного результата (при нечетном частном).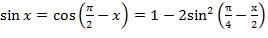 (1)
(1)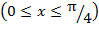 и
и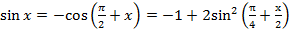 (2)
(2) .
.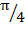 , либо
, либо 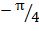 .
.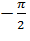 ≤ x ≤
≤ x ≤  :
: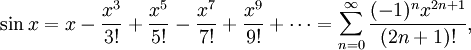
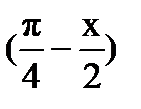 разложение в ряд Тейлора будет иметь следующий вид:
разложение в ряд Тейлора будет иметь следующий вид: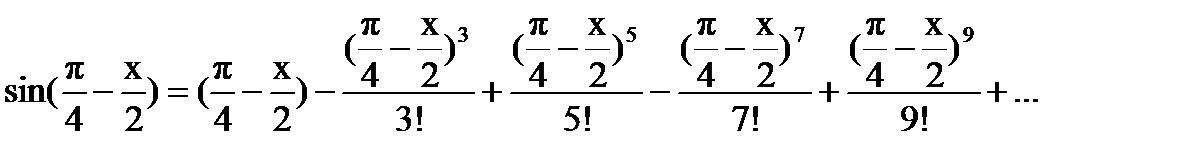
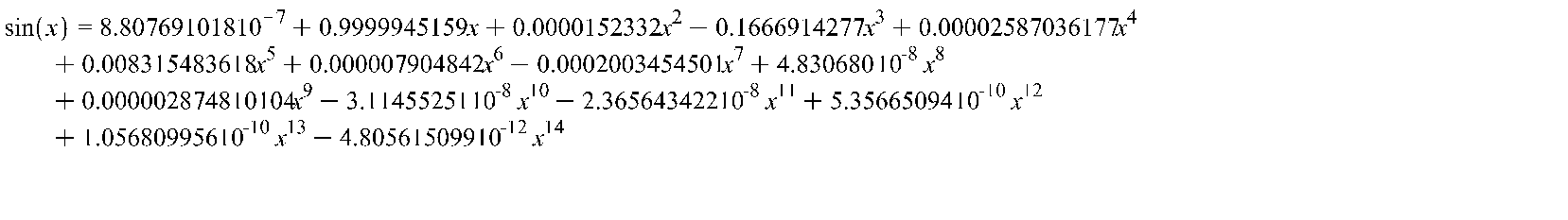
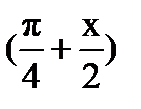 , будет иметь следующий вид:
, будет иметь следующий вид: