
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление скользящего среднего. Свойства скользящего среднего. Оценка сезонной компоненты с использованием скользящего среднего.Содержание книги
Поиск на нашем сайте
О методе скользящих средних. Метод скользящих средних — один из самых старых и широко известных способов сглаживания временного ряда. Он основан на переходе от начальных значений ряда к их средним значениям на интервале времени, длина которого выбрана заранее. При этом сам выбранный интервал времени скользит вдоль ряда. Получаемый таким образом ряд скользящих средних ведет себя гораздо более гладко, чем исходный ряд, за счет усреднения отклонений исходного ряда. Таким образом эта процедура дает представление обобщей тенденции поведения ряда. Ее применение особенно полезно для рядов с сезонными колебаниями и неясным характером тренда. В частности, переход к ряду скользящих средних может быть использован для выявления сезонной компоненты (или сезонного индекса) временного ряда. Вид средних. Применяя метод скользящих средних, можно использовать различные виды усредения значений ряда: среднее арифметическое (простое или с некоторыми весами), медианы и др. К сглаживанию с помощью медианы (медианное сглаживание) прибегают тогда, когда среди наблюдений есть выбросы (резко выделяющиеся данные). Вычисление скользящего среднего. Дадим формальное определение скользящего среднего сначала для интервалов сглаживания, длина которых выражается нечетными числами. Причина, по которой четные и нечетные длины рассматриваются порознь, выяснится чуть ниже. Пусть p = 2m + 1. Обозначим через xt результат усреднения элементов ряда
Если обсуждаемое среднее есть среднее арифметическое, то
Для медианного сглаживания
Для четных p = 2m определение несколько сложнее. Причина в том, что вычисленное по аналогичным формулам (как среднее арифметическое, медиана и т.д.) усредненное значение нельзя сопоставить какому-либо определенному моменту времени t. Например, среднее арифметическое
Выражение задает величину простого скользящего среднего Свойства скользящего среднего. Скользящее среднее, сглаживая исходный ряд, дает представление об общей тенденции поведения ряда — его тренде и циклической компоненте. Сделаем несколько замечаний о его свойствах. 1. При применении метода скользящих средних выбор величины интервала сглаживания должен делаться из содержательных соображений и привязываться к периоду сезонности для сезонных данных. Если процедура скользящего среднего используется для сглаживания несезонного ряда, то чаще всего величину интервала сглаживания выбирают равной трем, пяти или семи. Чем больше интервал усреднения, тем более гладкий вид имеет график скользящих средних. 2. Соседние члены ряда скользящих средних сильно коррелированы, так как в их формировании участвуют одни и те же члены исходного ряда. Это может приводить, к тому, что ряд скользящих средних может содержать циклические компоненты, отсутствующие в исходном ряде. Это явление носит название эффекта Слуцкого_Юла. 3. В качестве метода усреднения, кроме упомянутых выше среднего арифметического и медианы, можно рассматривать взвешенные скользящие средние, когда значения исходного ряда суммируется с определенными весами. Подобные процедуры целесообразны, если изменение временного ряда во времени носит явно нелинейный характер. Оценка сезонных компонент. Предположим, что наблюдаемый временной ряд имеет структуру Порядок оценки сезонных компонент в этом случае, в целом, аналогичен рассмотренному в п. 12.3.2. Только вместо оценки тренда методом наименьших квадратов мы будем использовать скользящее среднее в качестве совместной оценки тренда и циклической компоненты. Обозначим через ˆxt скользящее среднее с периодом p, построенное по ряду xt. Для упрощения обозначений начнем нумерацию величин ˆxt с единицы, так что ряд из скользящих средних есть: ˆx1, ˆx2,..., ˆxk. Соответственно изменим нумерацию исходного ряда так, чтобы величине ˆxt соответствовал член xt. (При этом приходится отбросить [p/2] первых членов исходного ряда, для которых значения ˆxt не определены. Здесь через [p/2] обозначена целая часть от деления p пополам.) Ради простоты предположим, что k = (m + 1)p, где m — положительное целое число. (Обратим внимание, что общая длина n исходного ряда при этом равна n = (m + 2)p при четном p и n = (m + 2)p − 1 при нечетном p.) Для каждого сезона
Каждое из этих отклонений xi от ˆxi можно рассматривать как результат влияния сезонных изменений. Усреднение этих разностей дает нам оценку сезонной компоненты si. В качестве простейшей оценки можно взять простое среднее, т.е. положить
Как и выше, вместо простого среднего можно взять взвешенное среднее, цензурированное среднее, медиану и т.д., для уменьшения влияния резко выделяющихся наблюдений. Для мультипликативной модели временного ряда, когда
К ряду yt можно применить изложенную выше методику, начиная с вычисления скользящих средних и кончая составлением оценки ˆri для ri. Оценкой для исходной величины si = eri будет служить eˆri, если log x — натуральный логарифм x, либо ˆsi = 10ˆri, если наши логарифмы десятичные. Удаление сезонной компоненты. Оно проводится так же, как и в разобранном выше случае. Для аддитивной модели удаление сезонной компоненты сводится к вычитанию оцененной сезонной компоненты из исходного ряда. Для мультипликативной модели эта процедура заключается в делении значений исходного ряда на соответствующие сезонные индексы.
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.007 с.) |


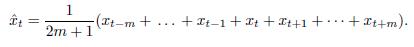

 следовало бы сопоставить моменту времени t = (2m + 1)/2, но такого момента во временном ряде нет. А это сильно осложняет дальнейшее выделение сезонных эффектов. Поэтому при четном интервале сглаживания 2m в усреднении задействуют не 2m, а 2m+1 значений временного ряда, но значения на краях интервала сглаживания берут с весами 1/2. Так, при использовании для усреднения среднего арифметического получается следующая формула:
следовало бы сопоставить моменту времени t = (2m + 1)/2, но такого момента во временном ряде нет. А это сильно осложняет дальнейшее выделение сезонных эффектов. Поэтому при четном интервале сглаживания 2m в усреднении задействуют не 2m, а 2m+1 значений временного ряда, но значения на краях интервала сглаживания берут с весами 1/2. Так, при использовании для усреднения среднего арифметического получается следующая формула: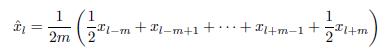
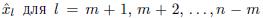 при четной величине интервала сглаживания p = 2m.
при четной величине интервала сглаживания p = 2m.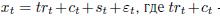 —тренд и циклическая составляющая, st — сезонная составляющая, а εt — случайная составляющая ряда. Пусть p — период последовательности st, так что st = st+p для всякого t. Пусть величина p нам известна. Мы хотим оценить значения st по наблюдениям xt.
—тренд и циклическая составляющая, st — сезонная составляющая, а εt — случайная составляющая ряда. Пусть p — период последовательности st, так что st = st+p для всякого t. Пусть величина p нам известна. Мы хотим оценить значения st по наблюдениям xt. , рассмотрим все относящиеся к нему разности
, рассмотрим все относящиеся к нему разности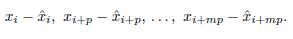


 целесообразно перейти к логарифмам
целесообразно перейти к логарифмам  . Тогда
. Тогда



