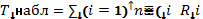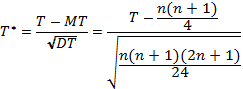Приближение для больших выборок.

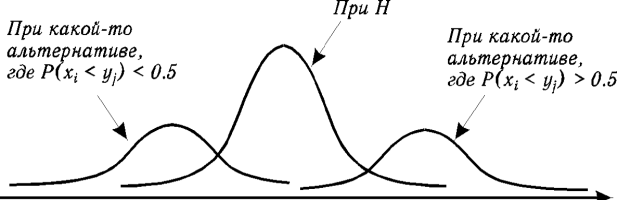
На практике часто приходится сталкиваться с ситуацией, когда объемы выборок m и n выходят за пределы, приведенные в таблицах. В этом случае используют аппроксимацию распределения W предельным распределением статистики W при m→∞ и n→∞. Перейдем от величины W к W^* = (W −MW)/√DW.

MW = n(m + n + 1)/2, DW = mn(m + n + 1)/12. Доказано, что в условиях H, при больших m, n случайная величина W^* распределена приблизительно по нормальному закону с параметрами (0, 1).

Обозначим через zα верхнее критическое значение стандартного нормального распределения. Его можно найти с помощью таблицы квантилей нормального распределения для любого 0 < α < 0.5. Благодаря симметрии распределения нижнее критическое значение равно −zα. Правило проверки H перефразируем так:

• отвергнуть H на уровне α против альтернативы P(x_i < y_j) > 0.5,

если W^*набл. ³ zα;

• отвергнуть H на уровне α против альтернативы P(x_i < y_j) < 0.5,

если W^*набл. ≤ −zα;

• отвергнуть H на уровне 2α против альтернативы P(x_i < y_j) =0.5, если |W^*_набл.| ³ z_α.

Правило, связанное с вычислением наименьшего уровня значимости, при использовании нормального приближения выглядит так: отвергнуть H (против соответствующих альтернатив), если оказывается малой вероятность 1 − Φ(W*набл.) для альтернативы P(x_i < y_j) > 0.5,

Φ(W*набл.) для альтернативы P(x_i < y_j) < 0.5, и 2Φ(|W*набл.|) − 1 для альтернативы P(x_i < y_j) = 0.5, где Φ(u) — функция нормального распределения (функция Лапласа), равная

Совпадения. Мы описали критерий Уилкоксона для проверки гипотезы об однородности двух выборок в условиях, когда функции распределений данных непрерывны и, тем самым, в выборках не должно быть совпадающих наблюдений. Однако на практике совпадающие наблюдения — не редкость. Чаще всего это происходит не потому, что нарушается условие непрерывности, а из-за ограниченной точности записи результатов измерений (например, рост человека обычно измеряется с точностью до 1 см). Применение критерия Уилкоксона к таким данным приводит к приближенным выводам, точность которых тем ниже, чем больше совпадающих значений.

Когда среди наблюдений встречаются одинаковые, им приписываются средние ранги. По определению, средний ранг числа z_i в совокупности чисел z₁, z₂,..., z_n есть среднее арифметическое из тех рангов, которые были бы назначены z_i и всем остальным значениям, совпадающим с z_i, если бы они оказались различными. После такого назначения рангов применяются описанные ранее процедуры.

Упомянутые группы одинаковых наблюдений называют связками. Количество элементов в связке называют ее размером. Наличие связей влияет на асимптотические распределения статистики Уилкоксона. Так, при использовании нормальной аппроксимации следует в формуле для вычисления W* заменить DW на

 

где t₁, t₂,..., t_g — размеры наблюденных связок среди игреков, g — общее число связок среди игреков. Наблюдение, не совпавшее с каким"либо другим наблюдением, рассматривается как связка размера 1, и в формуле, заменяющей DW, не учитывается.

При больших по размеру связках и (или) большом их числе применение критерия Уилкоксона сомнительно.

 

Проверка статистических гипотез. Критерий знаков для анализа парных повторных наблюдений.

Первая часть – см. стр.1.

Парные повторные наблюдения – эксперименты над одной партией, или партиями, схожими друг с другом.

Назначение. Критерий знаков используется для проверки гипотезы об однородности наблюдений внутри каждой пары (иногда говорят — для проверки гипотезы об отсутствии эффекта обработки).

Данные. Рассмотрим совокупность случайных пар (x₁, y₁),..., (x_n, y_n) объема n. Введем величины z_i = y_i − x_i, i = 1,...,n.

Допущения. 1. Все z_i предполагаются взаимно независимыми. Заметим, что мы не требуем независимости между элементами x_i и y_i c одинаковым номером i. Это весьма важно на практике, когда наблюдения делаются для одного объекта и тем самым могут быть зависимы.

2. Все z_i имеют равные нулю медианы, т.е. P(z_i < 0) = P(z_i >0) = 1/2. Подчеркнем, что законы распределения разных z_i могут не совпадать.

Гипотеза. Утверждение об отсутствии эффекта обработки для повторных парных наблюдений (x₁, y₁),..., (x_n, y_n) можно записать в виде H: P(x_i < y_i) = P(x_i > y_i) = 0.5 для всех i = 1,..., n.

Метод.

1. Перейдем от повторных парных наблюдений (x₁, y₁),..., (x_n, y_n) к величинам z_i, i = 1,..., n, введенным выше.

2. К совокупности z_i, i = 1,..., n применим критерий знаков для проверки гипотезы о равенстве нулю медиан распределений величин z_i, i = 1,..., n.

Приближение для больших совокупностей. Следует воспользоваться нормальной аппроксимацией биномиального распределения.

Связанные данные. Если среди значений z_i есть нулевые, то их следует отбросить и соответственно уменьшить n до числа ненулевых значений z_i.

Оценка эффекта обработки. Нередко для z_i рассматривают модель z_i = θ + e_i, i = 1,..., n, где e_i — ненаблюдаемые случайные величины, θ — некоторая константа, характеризующая положение одного распределения относительно другого (скажем, до воздействия и после). Эту константу часто именуют эффектом обработки. Принятые выше допущения 1 и 2 переносятся на величины e₁,..., e_n. Гипотеза однородности формулируется в виде гипотезы о нулевом эффекте обработки H: θ = 0.

Введенные величины θ и представления z_i = θ + e_i оказываются полезными, если в ходе проверки гипотезы выясняется, что θ = 0 и что поэтому надо оценить количественно то различие, которое привносит обработка (воздействие).

 

4. Проверка статистических гипотез. Анализ повторных парных наблюдений с помощью знаковых рангов (критерий знаковых ранговых сумм Уилкоксона).

Первая часть – см. стр.1.

Этот критерий является более мощным, чем критерий знаков.

Метод. 1. Вычислим абсолютные разности |z1|,..., |zn|. Пусть R_i обозначает ранг z_i в совместном упорядочении |z1|,..., |zn| от меньшего к большему.

2. Определим переменные ψi, i = 1,..., n, где

3. Вычислим наблюденное значение

 

4. Для одностороннего критерия для проверки H: P(zi < 0) = P(zi > 0) против правосторонней альтернативы P(zi < 0) < P(zi > 0) на уровне значимости α:

• отклонить H, если Tнабл. ³ t(α, n);

• принять H, если Tнабл. < t(α, n),

где критическое значение t(α, n) удовлетворяет уравнению P(T ³ t(α, n) |H) = α. Для одностороннего критерия для проверки той же гипотезы против левосторонней альтернативы P(zi < 0) > P(zi > 0) на уровне значимости α:

• отклонить H, если Tнабл. ≤ n(n+1)/2− t(α, n);

• принять H, если Tнабл. > n(n+1)/2− t(α, n).

Для двустороннего критерия для проверки той же гипотезы H против двусторонних альтернатив P(zi < 0) = P(zi > 0) на уровне значимости 2α:

• отклонить H, если Tнабл. ³ t(α, n) или Tнабл. ≤ n(n+1)/2− t(α, n);

• принять H, если n(n+1)/2− t(α, n) < Tнабл. < t(α, n).

Приближение для большой выборки. При выполнении гипотезы H статистика

имеет асимптотическое (при n→∞) распределение N(0, 1). Приведем приближение нормальной теории для проверки H, для определенности, против правосторонней альтернативы: H отклоняется, если T_набл. ³ z_α, в противном случае H принимается. Здесь z_α —квантиль уровня (1−α) стандартного нормального распределения N(0, 1). Остальные правила трансформируются аналогично.

Совпадения. Если среди значений z_i есть нулевые, то их следует отбросить, соответственно уменьшив n до количества ненулевых значений z_i. Если среди ненулевых значений |z_i| есть равные, то для вычисления T надо использовать средние ранги для величин |z₁|,..., |z_n| и далее использовать те же методы, что и без совпадений. Для приближения для больших выборок рекомендуется в формуле для вычисления T^* значение DT заменить на

где g — число связок, t₁,..., t_g — их размеры.