
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интервальные оценки параметров распределенияСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение 1. Интервальной называют оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр. Доверительным называют интервал, который с заданной вероятностью (надежностью) Интервальной оценкой с надежностью
где
При неизвестном
где Интервальной оценкой с надежностью
где Интервальной оценкой с надежностью
где
где
события);
Замечание. При больших значениях
Пример 1. Из генеральной совокупности извлечена выборка объема
Требуется оценить с надежностью 0,95 математическое ожидание нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала. Решение. Выборочную среднюю и «исправленное» среднее квадратическое отклонение найдем соответственно по формулам
Подставим в эти формулы данные задачи:
Таким образом, получим Найдем искомый доверительный интервал:
Значение Подставляя
Получили доверительный интервал Пример 2. По данным выборки объема Решение. Задача сводится к отысканию доверительного интервала
Значение
отсюда
Таким образом, полученный доверительный интервал Часто используют также следующие выборочные характеристики.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.13.119 (0.005 с.) |

 покрывает заданный параметр.
покрывает заданный параметр. нормально распределенного признака
нормально распределенного признака  по выборочной средней
по выборочной средней  при известном среднем квадратическом отклонении
при известном среднем квадратическом отклонении  генеральной совокупности служит доверительный интервал
генеральной совокупности служит доверительный интервал ,
, – точность оценки,
– точность оценки,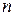 – объем выборки,
– объем выборки, – значение аргумента функции Лапласа
– значение аргумента функции Лапласа  (см. приложение 2), при котором
(см. приложение 2), при котором 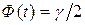 .
. ) доверительным будет интервал
) доверительным будет интервал ,
, – «исправленное» выборочное среднее квадратическое отклонение,
– «исправленное» выборочное среднее квадратическое отклонение,  находят по таблице приложения 3 по заданным
находят по таблице приложения 3 по заданным  при
при  ,
, при
при  ,
,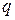 находят по таблице приложения 4 по заданным
находят по таблице приложения 4 по заданным  биномиального распределения по относительной частоте
биномиального распределения по относительной частоте  служит доверительный интервал (с приближенными концами
служит доверительный интервал (с приближенными концами  и
и  ):
): ,
, ,
,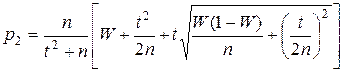 .
. (
( – число появлений
– число появлений ,
,  .
. :
:
 ,
,  .
. ,
,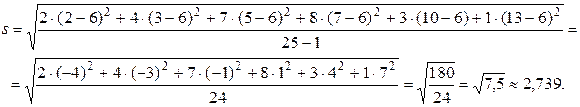
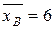 ,
,  .
. .
. находят по таблице приложения 3 по заданным
находят по таблице приложения 3 по заданным 
 :
:  .
.

 .
. , покрывающий неизвестное математическое ожидание
, покрывающий неизвестное математическое ожидание  из генеральной совокупности найдено «исправленное» среднее квадратическое отклонение
из генеральной совокупности найдено «исправленное» среднее квадратическое отклонение  нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение
нормально распределенного количественного признака. Найти доверительный интервал, покрывающий генеральное среднее квадратическое отклонение  (если
(если 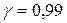 :
:  . Так как
. Так как  , то воспользуемся первым соотношением. Подставим
, то воспользуемся первым соотношением. Подставим  ,
,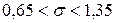 .
. – ошибка средней (среднее квадратическое отклонение выборочной средней от генеральной средней);
– ошибка средней (среднее квадратическое отклонение выборочной средней от генеральной средней); – коэффициент вариации (доля среднего квадратического отклонения в выборочной средней, в процентах).
– коэффициент вариации (доля среднего квадратического отклонения в выборочной средней, в процентах).


