
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение типовых задач по математической статистикеСодержание книги
Поиск на нашем сайте
Задача 1. В течение 300 дней фиксировалась цена акции ООО «Психолог». Затем была проведена случайная выборка объёмом n=20, и получены следующие результаты: 35,9; 35,3; 42,7; 45,3; 25,6; 35,3; 33,4; 27,0; 35,9; 38,8; 33,7; 38,6; 40,8; 35,5; 44,1; 37,4; 34,2; 30,8; 38,4; 31,3. Требуется получить вариационный ряд и построить гистограмму относительных частот; найти основные выборочные характеристики: Решение. Запишем исходные данные в виде ранжированного ряда, то есть, располагая их в порядке возрастания: 25,6; 27,0; 30,8; 31,3; 33,4; 33,7: 34,2; 35,3; 35,3; 35,5; 35,9; 35,9; 37,4; 38,4; 38,6; 38,8; 40,8; 42,7; 44,1; 45,3. Максимальное значение признака составляет 45,3 ц, а минимальное – 25,6 ц. Разница между ними составляет 19,7 ц. Этот интервал надо разбить на определенное количество частей. При малом объеме выборки (20–40 вариант) намечают 4–7 интервалов. Возьмем длину интервала Теперь найдем относительные частоты попадания вариант выборки в каждый интервал:
Для проверки вычисляем сумму относительных частот:
Тот факт, что в сумме получена единица, подтверждает правильность вычислений. Вычислим плотности
Полученные результаты сведем в таблицу 4. Таблица 4.
Строим гистограмму относительных частот – ступенчатую фигуру, состоящую из прямоугольников, основаниями которых являются интервалы, а высотами соответствующие значения плотности относительных частот.
Рис.8. Гистограмма относительных частот. Так как объем выборки небольшой ( Основные выборочные характеристики вычисляются по формулам: Таблица 5.
Подставляя полученные значения в формулы, получаем
Доверительный интервал для оценки генеральной средней имеет вид:
Вычисляем теперь точность оценки
где значение Таким образом, с надежностью 95% можно утверждать, что средняя цена акции за 300 дней заключена в пределах от Задача 2. Для определения средней урожайности сахарной свеклы в агрофирме на площади
Требуется найти: 1) величину, которую следует принять за среднюю урожайность на всем массиве; 2) величину, которую следует принять за среднее квадратическое отклонение урожайности на всем массиве; 3) доверительный интервал, в котором с вероятностью Решение. В качестве приближенного значения средней урожайности на всем массиве принимаем среднюю арифметическую данного распределения, то есть выборочную среднюю. За значения признака нужно принять середины интервалов. Получим:
= 3200/100 = 32. Для оценки дисперсии генеральной совокупности вычисляем исправленное среднее квадратическое отклонение:
Отсюда можно найти среднее квадратическое отклонение урожайности на всем массиве
Найдем среднее квадратическое отклонение выборочной средней по формуле
Итак, оценка средней урожайности сахарной свеклы на всем массиве равна 32 ц со средней квадратической ошибкой 0,34 ц. Оценка среднего квадратического отклонения урожайности на всем массиве равна 3,4 ц. Для вычисления доверительного интервала воспользуемся двойным неравенством:
Так как
Концы доверительного интервала:
Таким образом, с вероятностью 0,95 средняя урожайность сахарной свеклы на всем массиве заключена в границах от 31,33 ц до 32,67 ц.
ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ
Определение 1. Зависимость двухслучайных величин называют корреляционной, если изменение одной случайной величины приводит к изменению среднего значения другой случайной величины. Основные задачи теории корреляции: 1. определить есть ли связь между случайными величинами, если есть, то найти уравнение зависимости (уравнение регрессии); 2. определить силу (тесноту) связи между случайными величинами. Для определения самого факта связи между случайными величинами и тесноты связи служит коэффициент корреляции. Уравнение регрессии позволяет предсказать, какие изменения в среднем будет претерпевать признак при изменении другого признака. Если уравнения регрессии являются линейными, то есть графиками будут прямые линии, то корреляционная зависимость называется линейной. Пусть извлечена выборка объема
Выборочный коэффициент корреляции
Свойства выборочного коэффициента корреляции: 1. Значения коэффициента корреляции изменяются на отрезке [–1;1]:
2. Чем модуль 3. Если 4. Если 5. Если Выборочное уравнение прямой регрессии
где
Выборочное уравнение прямой регрессии
Пример. Психологи провели тестирование среди пациентов психоневрологического диспансера. Возраст пациентов колебался от 14 до 34 лет. Затем была проведена случайная выборка объёмом n=10. Была поставлена задача: определить есть ли зависимость возраста испытуемого
Таблица 6.
Требуется вычислить выборочный коэффициент корреляции и найти выборочное уравнение прямой регрессии Решение. Вычислим выборочный коэффициент корреляции по формуле:
Для вычисления величин, входящих в формулу, составим вспомогательную таблицу 7, в которой результаты измерений записаны столбцами. Внизу каждого из столбцов вычислены суммы для нахождения средних Таблица 7.
Находим выборочные средние
Выполнив все вычисления в таблице (3 – 7 столбцы), получаем:
Подставляя эти значения в соответствующую формулу, вычислим коэффициент корреляции:
Таким образом, Найдем теперь выборочное уравнение прямой регрессии
где
Тогда Подставляя в выборочное уравнение прямой регрессии Окончательно,
искомое уравнение прямой регрессии
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.98.61 (0.009 с.) |

 ,
, 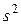 , s,
, s,  ,
,  ; с надежностью
; с надежностью  указать доверительный интервал для оценки генеральной средней.
указать доверительный интервал для оценки генеральной средней.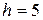 . Получаем пять интервалов: первый 25 – 30, второй 30 – 35, третий 35 – 40, четвертый 40 – 45, пятый 45 – 50. С помощью ранжированного ряда определим частоту попадания вариант выборки в каждый интервал. В первый интервал 25 – 30 попадают два значения: 25,6 и 27,0; поэтому
. Получаем пять интервалов: первый 25 – 30, второй 30 – 35, третий 35 – 40, четвертый 40 – 45, пятый 45 – 50. С помощью ранжированного ряда определим частоту попадания вариант выборки в каждый интервал. В первый интервал 25 – 30 попадают два значения: 25,6 и 27,0; поэтому 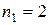 . Во второй интервал попадают пять значений, поэтому
. Во второй интервал попадают пять значений, поэтому 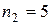 . Аналогично,
. Аналогично, 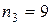 ,
, 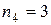 ,
,  .
.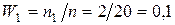 ;
; 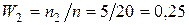 ;
; 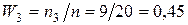 ;
;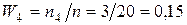 ;
; 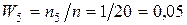 .
.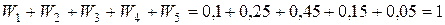 .
. относительных частот вариант. Получаем
относительных частот вариант. Получаем ;
;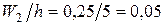 ;
;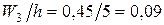 ;
;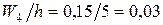 ;
;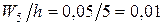 .
.
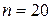 ) и почти все наблюдаемые значения различны, то для вычисления выборочных характеристик составим вспомогательную таблицу (таблица 5).
) и почти все наблюдаемые значения различны, то для вычисления выборочных характеристик составим вспомогательную таблицу (таблица 5).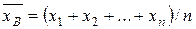 – выборочная средняя;
– выборочная средняя;  – «исправленная» дисперсия;
– «исправленная» дисперсия;  – «исправленное» среднее квадратическое отклонение;
– «исправленное» среднее квадратическое отклонение;  – ошибка средней;
– ошибка средней;  – коэффициент вариации.
– коэффициент вариации.
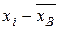
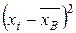
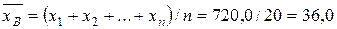 ;
; ;
; ;
;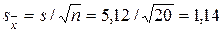 ;
; .
. .
.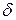 :
: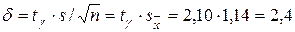 ;
; находим по таблице приложения 3.
находим по таблице приложения 3.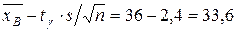 ц. (гарантированный минимум) до
ц. (гарантированный минимум) до  ц. (возможный максимум).
ц. (возможный максимум). га была определена ее урожайность на 100 га. Результаты выборочного обследования представлены следующим распределением:
га была определена ее урожайность на 100 га. Результаты выборочного обследования представлены следующим распределением: заключена средняя урожайность на всем массиве.
заключена средняя урожайность на всем массиве.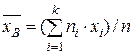 = (24∙3+26∙10+28∙6+30 ∙16+32 ∙15+34∙30+36∙ 20)/100 =
= (24∙3+26∙10+28∙6+30 ∙16+32 ∙15+34∙30+36∙ 20)/100 =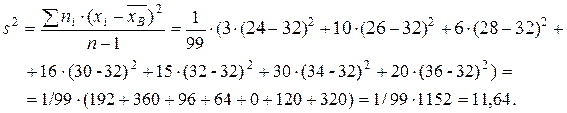
 =
=  = 3,4.
= 3,4.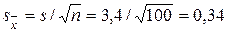 ц.
ц. .
. , то значение
, то значение  найдем из условия
найдем из условия  . По таблице приложения 2 находим значение
. По таблице приложения 2 находим значение 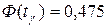 и
и  , следовательно, получаем:
, следовательно, получаем: .
.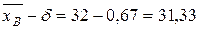 и
и 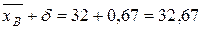 .
. и исследуются два количественных признака
и исследуются два количественных признака  и
и 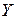 . Результаты измерений занесены в таблицу.
. Результаты измерений занесены в таблицу.

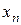
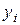
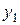

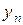
 находится по формуле:
находится по формуле: .
.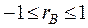 .
.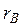 больше и ближе к 1, тем теснее связь между изучаемыми признаками.
больше и ближе к 1, тем теснее связь между изучаемыми признаками.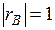 , то между признаками функциональная связь.
, то между признаками функциональная связь. , то между изучаемыми признаками нет линейной корреляционной зависимости.
, то между изучаемыми признаками нет линейной корреляционной зависимости. , то между признаками прямая (положительная) связь и если
, то между признаками прямая (положительная) связь и если 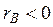 , то между признаками обратная (отрицательная) связь.
, то между признаками обратная (отрицательная) связь. ,
,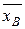 ,
, 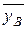 – выборочные средние. За приближенные значения
– выборочные средние. За приближенные значения 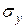 и
и  принимают соответственно
принимают соответственно 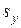 :
: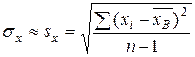 ,
,  .
.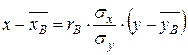 .
. от значения показателя развития заболевания
от значения показателя развития заболевания 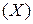 . Результаты этого измерения представлены в таблице 6:
. Результаты этого измерения представлены в таблице 6: .
.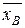 и
и 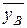 . Далее расположены столбцы, в которых вычисляются разности
. Далее расположены столбцы, в которых вычисляются разности  , их квадраты и произведения. Значения этих столбцов суммируются (последняя строка), чтобы получились величины, необходимые для подстановки в формулу. Отметим, что суммы в столбцах, в которых вычислены разности
, их квадраты и произведения. Значения этих столбцов суммируются (последняя строка), чтобы получились величины, необходимые для подстановки в формулу. Отметим, что суммы в столбцах, в которых вычислены разности 
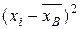
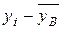
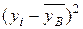

 = 700/10 = 70,
= 700/10 = 70,  = 230/10 = 23.
= 230/10 = 23.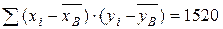 ,
,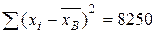 ,
, .
.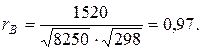
 выбранных пациентов имеет место очень сильная (т.к. значение
выбранных пациентов имеет место очень сильная (т.к. значение  близко к 1) и положительная (т.к.
близко к 1) и положительная (т.к. 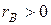 ) корреляция между возрастом испытуемого
) корреляция между возрастом испытуемого 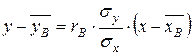 ,
, ,
, 
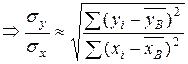 .
.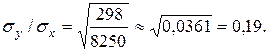
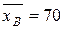 ,
, 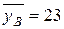 ,
, 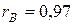 ,
, 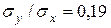 , получим
, получим 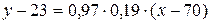 или
или 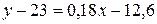 .
. –
–


