Часть 8. Подбор параметра и таблицы подстановки

Решение задач – одно из важных применений Excel. Системы линейных уравнений решаются с помощью матриц, задачи оптимизации с одним неизвестным с помощью инструмента Подбор параметра, задачи оптимизации со многими неизвестными с помощью инструмента Поиск решения, задачи прогнозирования и статистического анализа данных с помощью пакета Анализ данных и т.д.

Инструмент Подбор параметра позволяет методом последовательных итераций найти приближенное решение некоторой целевой функции (уравнения) с одним неизвестным.

 

Пример 1. Решить уравнение 2х³-3х²+х-5=0.

 

1. Ячейку А2 используем для хранения неизвестного Х и запишем в нее 0. В ячейку В2 запишем уравнение, как показано ниже:

 

2. Встаньте на ячейку с формулой В2 и вызовите инструмент вызовите его – С е рвисà П одбор параметра… В открывшемся окне введите адрес изменяемой ячейки $A$2 и искомое значение функции 0, как показано:

 

 

3. После нажатия ОК Вы получите решение:

 

 

Найденное решение приближенное, поэтому можно считать, что при х=1,918578609 значение уравнения 2х³-3х²+х-5 стремится к нулю, т.е. к 0,000107348. Смело установите для ячеек А2 и В2 числовой формат отображения данных и получите следующее:

 

Следует отметить, что уравнение может иметь более одного решения. Поэтому рекомендуется выполнить подбор параметра для разных начальных значений Х, указывая положительные, отрицательные, большие и малые значения. В нашем примере установите начальное значение А2=–1 и повторите подбор. Решение будет таким же.

 

 

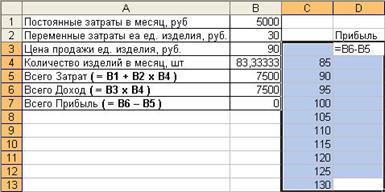
Пример 2. Фирма производит изделия и продает их по цене 90руб. Ежемесячные постоянные затраты составляют 5000руб., переменные затраты на единицу изделия – 30руб. Требуется:

a) определить количество изделий для получения прибыли 3000руб.;

b) определить точку безубыточности, т.е. вычислить количество изделий, при котором прибыль равна 0;

c) определить изменение прибыли для 10 следующих значений количества с шагом 5, а также прибыль при этих значениях количества для цен 80, 85, 95 и 100руб.

В первую очередь, запишите исходные данные и формулы в Excel наиболее удобным образом для будущего решения:

 

 

В ячейках В5, В6 и В7 записаны формулы. Для решения п. а) задачи, встаньте на ячейку с формулой прибыли В7 и запустите инструмент Подбор параметра:

 

 

Результат подбора будет выглядеть так – т.е. для получения прибыли в 3000руб/мес необходимо изготовить и продать 133 изделия в месяц:

 

 

Решение п. b) задачи также находится просто. Поскольку в точке безубыточности вся Прибыль равна нулю (весь доход равен всем затратам), то в качестве целевого значения ячейки В7 в Подборе параметра следует ввести 0 – Значение количества получим 83 шт/мес:

 

 

 

Решение п. c) задачи с помощью Таблицы подстановки. Вначале рассчитаем 10 значений прибыли для следующих значений количества с шагом 5. Используем для этого таблицу подстановки с одним изменяемым параметром. Подготовьте исходные данные: в ячейки C4:C13 запишите значения количества с шагом 5, а в колонке справа в строке выше (ячейка D3) - формулу из ячейки В7:

 

 

Примените инструмент Таблица подстановки к выделенным данным (диапазон C3:D13) – вызовите пункт Д анныеà Т аблица подстановки…, укажите изменяемую ячейку ($B$4) и порядок расположения исходных данных (в строках) в окне запроса (см. ниже). После нажатия ОК в ячейках D4:D13 будут рассчитаны значения прибыли:

 

 

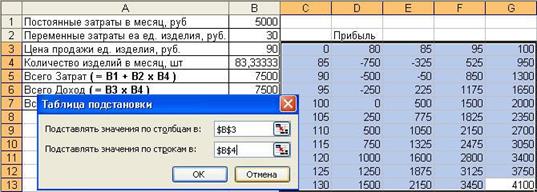
На последнем шаге рассчитаем значения прибыли для тех же значений количества при ценах 80, 85, 95 и 100руб. Используем для этого таблицу подстановки с двумя изменяемыми параметрами.

Подготовьте исходные данные: в ячейки C4:C13 запишите значения количества, в строке D3:G3 запишите значения цен, на пересечении строки и столбца с данными в ячейке C3 запишите формулу из ячейки В7:

 

 

 

Примените инструмент Д анныеà Т аблица подстановки…, к выделенным данным (диапазон C3:G13). Укажите изменяемые ячейки по строкам ($B$4) и по столбцам ($B$3) в окне запроса – после нажатия ОК в ячейках D4:G13 будут рассчитаны значения прибыли:

 

 

 

Часть 9. Поиск решения

Для численного решения уравнений со многими неизвестными и ограничениями в Excel включен инструмент Поиск решения.

 

По умолчанию инструмент не установлен и его следует установить: вставьте дистрибутивный CD-диск и выберите в списке надстроек С е рвисàНадстро й ки… соответствующий флажок.

 

Если целевая функция и ограничения линейны, то решение состоит в нахождении множества чисел (х₁, х₂, … х_n), минимизирующих (максимизирующих) линейную целевую функцию f(х₁, х₂, … х_n)= c₁х₁+c₂х₂+… +c_nх_n при m<n линейных ограничениях-равенствах а_i1х₁+а_i2х₂+… +а_inх_n (где i=1,2, … m) и n линейных ограничениях-неравенствах х_k>=0 (где k=1, 2, … n). Инструмент Поиск решения обеспечивает максимум 200 изменяемых ячеек х_i при поиске решения (n_мах=200).

В качестве содержательного примера рассмотрим задачу оптимизации туристических групп (экскурсионных пакетов). Российская туристическая фирма ежедневно отправляет в три отеля Анталии, Кемера и Мармариса (Турция) соответственно 30, 20 и 16 человек. Экскурсионная программа каждой группы состоит из рафтинга (спуск по горной реке на плоту), яхт-тура вдоль побережья и путешествия джип-сафари в турецкую глубинку. Стоимость экскурсий с трансфером на человека для отелей разных городов следующая:

 

	Рафтинг	Яхт-тур	Джип-сафари
Анталия
Кемер
Мармарис

 

При этом существуют ограничения на количество человек в экскурсии: рафтинг – 25 чел., яхт-тур – 20 чел., джип-сафари – 30 чел. От каждого отеля на каждую экскурсию должно быть послано не менее 5 чел.

Необходимо определить оптимальное количество туристов для участия в каждой экскурсии при заданных ограничениях. Под оптимальностью будем понимать минимизацию суммарных расходов турфирмы.

Приступим к ее решению. Постановка задачи выполнена достаточно четко. Переложим условие задачи на язык формул, т.е. опишем математическую модель. Введем обозначения подбираемых значений неизвестных х_i – число туристов каждого отеля на каждый вид экскурсии:

 

	Рафтинг	Яхт-тур	Джип-сафари
Анталия	х1	х2	х3
Кемер	х4	х5	х6
Мармарис	х7	х8	х9

 

В процессе решения надо найти такие х₁…х₉, чтобы получить при существующих ограничениях минимум целевой функции (стоимости), которая запишется так:

 

55х₁ + 20х₂ + 35х₃ + 65х₄ + 35х₅ + 20х₆ + 60х₇ + 25х₈ + 25х₉

 

Запишем ограничения в виде формул. Ограничения на ежедневное количество человек в экскурсиях по городам:

 

х₁ + х₂ + х₃ = 30 х₄ + х₅ + х₆ = 20 х₇ + х₈ + х₉ = 16

 

Ограничения на ежедневное количество мест по видам экскурсий:

х₁ + х₄ + х₇ <= 25 х₂ + х₅ + х₈ <=20 х₃ + х₆ + х₉ <=30

 

Другие ограничения – количество туристов от каждого отеля на экскурсию неделимо и больше 5: (х₁, х₂, … х₉) >= 5 и (х₁, х₂, … х₉) – целые числа

 

Теперь введем условие задачи – оптимизируемую модель в Excel в виде, наиболее удобном для дальнейших вычислений, как показано ниже:

 

 

Здесь, в ячейках G1:G9 размещены начальные значения неизвестных (х₁, х₂, … х₉)=0. В ячейках С3:С8 записаны граничные значения числа туристов от отелей и в экскурсиях. В ячейках D3:D8 записаны формулы-заготовки для ограничений: =G1+G2+G3, =G4+G5+G6, =G7+G8+G9, =G1+G4+G7, =G2+G5+G8, =G3+G6+G9. Целевая функция записана в ячейке В1: =55*G1+20*G2+35*G3+65*G4+35*G5+20*G6+60*G7+25*G8+25*G9.

Нам осталось запустить поиск решения С е рвисàПоиск р ешения… и ввести адреса ячеек и ограничения, как на рисунке:

 

 

Результат поиска решения выглядит так:

 

 

Здесь в ячейках G1:G9 подобрано оптимальное количество туристов, дающее минимальную стоимость расходов, равную 2295$. Проанализируйте полученное решение.

Поэкспериментируйте: попробуйте вручную изменить подобранные значения, оцените значения целевой функции. Повторно вызовите инструмент Поиск решения, удалив условие (х₁, х₂, … х₉) >= 5 или добавив новое условие, и выполните подбор.

Обобщим проделанную работу и выделим этапы решения задачи оптимизации со многими неизвестными в Excel с помощью инструмента Поиск решения:

· анализ задачи, выделение свойств, параметров, ограничений;

· математическое описание оптимизируемой модели – введение обозначений, ограничений и создание целевой функции;

· грамотное размещение модели и поиск решения в Excel.

 

Инструмент Поиск решения может применяться как для решения линейных, так и для других, нелинейных задач. По кнопке Параметры можно настраивать точность, допустимое отклонение от оптимума, метод экстраполяции (оптимизации) и другие параметры, можно загрузить или сохранить оптимизируемую модель. За подробностями обращайтесь к справке по F1.

 

В состав Excel входит файл с примерами использования инструмента Поиск решения Solvsamp.xls. Он обычно расположен в папке Program Files\Microsoft Office\Office11\Samples. Каждый лист содержит один из шести примеров — "Структура производства", "Транспортная задача", "График занятости", "Управление капиталом", "Портфель ценных бумаг" и "Проектирование цепи". В примерах уже подобраны целевая и влияющие ячейки, а также ограничения. Примеры из Solvsamp.xls помогут разрешить ваши вопросы.

Отметим, что инструмент Поиск решения работает аналогичным образом в программе Calc OpenOffice.