Поиск статистических зависимостей. Корреляция

 

Знание взаимосвязей между выборками важно для прогнозирования ситуации и принятия решений. Для оценки взаимосвязи между выборками (переменными X и Y) применяют регрессионный анализ, корреляционный и ковариационный анализ. Первый устанавливает форму взаимозависимости, вторые - степень связи выборок. Корреляцию применяют, когда выборки представлены в безразмерном виде (с разной размерностью), например вес и рост. Ковариацию можно применять для выборок с одинаковой размерностью, например продажи до рекламной компании и продажи после рекламной компании.

Степень связи двух выборок (случайных величин X и Y) оценивается ковариацией и коэффициентом корреляции R. Ковариация есть среднее произведений отклонений для каждой пары значений выборок. Коэффициент корреляции выборки представляет собой ковариацию двух выборок, деленную на произведение их стандартных отклонений (см. справку по F1).

Ковариация принимает значения в единицах анализируемых выборок. Коэффициент корреляции R принимает значения от –1 до 1. Если R =0 – зависимости нет, R >0 – зависимость прямо пропорциональная, R <0 – зависимость обратно пропорциональная.

Таким образом, корреляционный и ковариационный анализ дают возможность установить, ассоциированы ли выборки по величине, то есть, большие значения из одной выборки связаны с большими значениями другой выборки (положительная корреляция/ковариация), или, наоборот, малые значения одной выборки связаны с большими значениями другой (отрицательная корреляция/ковариация), или данные двух выборок никак не связаны (корреляция/ковариация близка к нулю).

Функции Excel КОРРЕЛ, КОВАР и инструменты Корреляция, Ковариация вычисляют степень линейной взаимозависимости между выборками. Если коэффициент корреляции |R|>0.6, то линейную зависимость между выборками считают выявленной, при |R|<0.4 – не выявленной.

Определим степень взаимосвязи между доходом семьи и числом посещений супермаркета в месяц – рис. 2.97. Тут же показан результат функции КОРРЕЛ(A2:A12;B2:B12)= –0.981225708. Это говорит о высокой степени обратной линейной зависимости между рассматриваемыми параметрами.

 

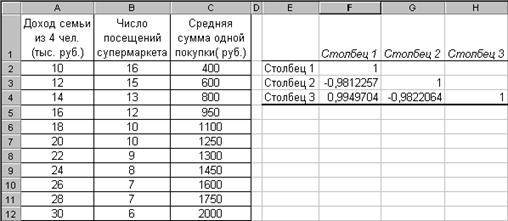
Рис. 2.97

Теперь добавим третий параметр – среднюю сумму одной покупки (рис. 2.98) и применим инструмент Корреляция: меню С е рвисàАна л из данных…. Параметры заполните как на рис. 2.99.

Результат показан в правой части рис. 2.98: в ячейках E1:H4 вычислена корреляционная матрица, на пересечении столбцов и строк которой записаны коэффициенты корреляции между параметрами (столбцами).

В результате анализа выявлены:

сильная степень обратной линейной зависимости между столбцом 1 и столбцом 2 (R = –0,9812257);

сильная степень прямой линейной зависимости между столбцом 1 и столбцом 3 (R = 0,99497);

сильная степень обратной линейной зависимости между столбцом 2 и столбцом 3 (R = –0,982206);

 

Рис. 2.98

 

Рис. 2.99

 

Задания для самостоятельного выполнения:

1. Определить степень взаимосвязи между валовым доходом и расходами компании, заданной следующими выборками:

 

Валовый доход (тыс. руб.)
Расходы (тыс. руб.)

 

 

2. Определить степень взаимосвязи между месяцами (сезонами) и доходами компьютерных и строительных компаний:

 

Янв

Фев

Мар

Апр

Май

Июн

Июл

Авг

Сен

Окт

Ноя

Дек

Доходы от компьютеров

Доходы от стройматериалов

 

 

Приложение 1. ФУНКЦИЯ ПРОПИСЬ()

 

Часто пользователю требуются возможности, которых нет в Excel или они реализованы не так, как нужно пользователю. Тогда у пользователя есть шанс написать свою собственную подпрограмму (функцию) на языке Visual Basic for Applications (VBA).

 

В качестве примера приведем полезную функцию ПРОПИСЬ(), которая выводит числа прописью. Например, ПРОПИСЬ(111)= "Сто одиннадцать". Функция включается в список функций Excel в группу Определенные пользователем и может вызываться через мастер функций fx. Применение функции ПРОПИСЬ() показано на рис. П.17.

 

Рис. П.17

 

Добавление новой функции выполняется в среде разработки VBA (рис. П.18), которая вызывается из Excel через пункт меню С е рвисà М акросà Р едактор Visual Basic (Alt+F11). Находясь в редакторе VBA, вставьте новый модуль (Вст а вкаà М одуль или I nsertà M odule) и в правом окне модуля введите текст программы, как показано на рис. П.18.

 

Рис. П.18

Запустить редактор VBA можно из панели Visual Basic, которую можно отобразить так: щелкните правой кнопкой мыши по Панели инструментов Excel и в списке отметьте Visual Basic.

 

 

Текст программы можно скачать из Интернета по адресу www.kuprava.ru в разделе Excel. Здесь приводим полный текст функции ПРОПИСЬ() на языке VBA с комментариями.