
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Систематизация факторов в анализе хозяйственной деятельностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Необходимость и значение систематизации факторов. Основные способы систематизации факторов в детерминированном и стохастическом анализе. Системный подход в АХД вызывает необходимость взаимосвязанного изучения факторов с учетом их внутренних и внешних связей, взаимодействия и соподчиненности, что достигается с помощью систематизации. Систематизация в целом — это размещение изучаемых явлений или объектов в определенном порядке с выявлением их взаимосвязи и соподчиненности. Одним из способов систематизации факторов является создание детерминированных факторных систем. Создать факторную систему — значит представить изучаемое явление в виде алгебраической суммы, частного или произведения нескольких факторов, определяющих его величину и находящихся с ним в функциональной зависимости. Например, объем валовой продукции промышленного предприятия можно представить в виде произведения двух факторов первого порядка: среднего количества рабочих и среднегодовой выработки продукции одним рабочим за год, которая в свою очередь зависит непосредственно от количества отработанных дней одним рабочим в среднем за год и среднедневной выработки продукции рабочим. Последняя также может быть разложена на продолжительность рабочего дня и среднечасовую выработку (рис. 5.2).
Развитие детерминированной факторной системы достигается, как правило, за счет детализации комплексных факторов. Элементные (в нашем примере — количество рабочих, количество отработанных дней, продолжительность рабочего дня) не раскладываются на сомножители, так как по своему содержанию они однородны. С развитием системы комплексные факторы постепенно детализируются на менее общие, те в свою очередь еще на менее общие, постепенно приближаясь по своему аналитическому содержанию к элементным (простым). Однако необходимо заметить, что развитие факторных систем до необходимой глубины связано с некоторыми методологическими трудностями и прежде всего с трудностью нахождения факторов общего характера, которые можно было бы представить в виде произведения, частного или алгебраической суммы нескольких факторов. Поэтому обычно детерминированные системы охватывают наиболее общие факторы. Между тем исследование более конкретных факторов в АХД имеет существенно большее значение, чем общих. Отсюда следует, что совершенствование методики факторного анализа должно быть направлено на взаимосвязанное изучение конкретных факторов, которые находятся, как правило, в стохастической зависимости с результативными показателями. Большое значение в исследовании стохастических взаимосвязей имеет структурно-логический анализ связи между изучаемыми показателями. Он позволяет установить наличие или отсутствие причинно-следственных связей между исследуемыми показателями, изучить направление связи, форму зависимости и т.д., что очень важно при определении степени их влияния на изучаемое явление и при обобщении результатов анализа. Анализ структуры связи изучаемых показателей в АХД осуществляется с помощью построения структурно-логической блок-схемы, которая позволяет установить наличие и направление связи не только между изучаемыми факторами и результативным показателем, но и между самими факторами. Построив блок-схему, можно увидеть, что среди изучаемых факторов имеются такие, которые более или менее непосредственно воздействуют на результативный показатель, и такие, которые воздействуют не столько на результативный показатель, сколько друг на друга. Например, на рис. 5.3 показана связь между себестоимостью единицы продукции растениеводства и такими факторами, как Урожайность культур, производительность труда, количество внесенного удобрения, качество семян, степень механизации производства.
Рис. 5. 3. Блок-схема стохастической факторной системы себестоимости продукции Прежде всего, необходимо установить наличие и направление связи между себестоимостью продукции и каждым фактором. Безусловно, между ними существует тесная связь. Непосредственное влияние на себестоимость продукции оказывает в данном примере только урожайность культур. Все остальные факторы влияют на себестоимость продукции не только прямо, но и косвенно, через урожайность культур и производительность труда. Например, количество внесенных удобрений в почву содействует повышению урожайности культур, что при прочих одинаковых условиях обусловливает снижение себестоимости единицы продукции. Однако необходимо учитывать и то, что увеличение количества внесенных удобрений приводит к росту суммы затрат на гектар посева. И если сумма затрат возрастает более высокими темпами, чем урожайность, то себестоимость продукции будет не снижаться, а повышаться. Значит, связь между этими двумя показателями может быть и прямой, и обратной. Аналогично влияет на себестоимость продукции и качество семян. Приобретение элитных, высококачественных семян вызывает рост суммы затрат. Если они возрастают в большей степени, чем урожайность от применения более высококачественных семян, то себестоимость продукции будет увеличиваться, и наоборот. Степень механизации производства влияет на себестоимость продукции и прямо, и косвенно. Повышение уровня механизации вызывает рост затрат на содержание основных средств производства. Однако при этом увеличивается производительность труда, растет урожайность, что содействует снижению себестоимости продукции. Исследование взаимосвязей между факторами показывает, что из всех изучаемых факторов отсутствует причинно-следственная связь между качеством семян, количеством удобрений и механизацией производства. Отсутствует также непосредственная обратная зависимость данных показателей от уровня урожайности культуры. Все остальные факторы, прямо или косвенно влияют друг на друга. Таким образом, систематизация факторов позволяет более глубоко изучить взаимосвязь факторов при формировании величины изучаемого показателя, что имеет очень важное значение на следующих этапах анализа, особенно на этапе моделирования исследуемых показателей.
5.4. Детерминированное моделирование и преобразование факторных систем Сущность и значение моделирования, требования к нему. Основные типы факторных детерминированных моделей. Способы преобразования факторных моделей. Правила моделирования. Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину. Моделирование — это один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Сущность его заключается в том, что взаимосвязь исследуемого показателя с факторными передается в форме конкретного математического уравнения. В факторном анализе различают модели детерминированные (функциональные) и стохастические (корреляционные). С помощью детерминированных факторных моделей исследуется функциональная связь между результативным показателем (функцией) и факторами (аргументами). При моделировании детерминированных факторных систем необходимо руководствоваться следующими правилами: 1. Факторы, включаемые в модель, и сами модели должны иметь явно выраженный характер, реально существовать, а не быть придуманными абстрактными величинами или явлениями. 2. Факторы, которые входят в систему, должны быть не только необходимыми элементами формулы, но и находиться в причинно-следственной связи с изучаемыми показателями. Иначе говоря, построенная факторная система должна иметь познавательную ценность. Факторные модели, которые отражают причинно-следственные отношения между показателями,,имеют значительно большее познавательное значение, чем модели, созданные при помощи приемов математической абстракции. Последнее можно проиллюстрировать следующим образом. Возьмем две модели: 1) ВП = ЧР × ГВ 2) ГВ = ВП/ЧР где ВП — валовая продукция предприятия; ЧР — численность работников на предприятии; ГВ — среднегодовая выработка продукции одним работником. В первой системе факторы находятся в причинной связи с результативным показателем, а во второй — в математическом соотношении. Значит, вторая модель, построенная на математических зависимостях, имеет меньшее познавательное значение, чем первая. 3. Все показатели факторной модели должны быть количественно измеримыми, т.е. должны иметь единицу измерения и необходимую информационную обеспеченность. 4. Факторная модель должна обеспечивать возможность измерения влияния отдельных факторов, это значит, что в ней должна учитываться соразмерность изменений результативного и факторных показателей, а сумма влияния отдельных факторов должна равняться общему приросту результативного показателя. В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей. 1. Аддитивные модели. Y = Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей. 2. Мультипликативные модели: Y = Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов. 3. Кратные модели: Y = Они применяются тогда, когда результативный показатель получают делением одного факторного показателя на величину другого. 4. Смешанные (комбинированные) модели — это сочетание в различных комбинациях предыдущих моделей: Y = (a +b) /c; Y = a /(b + c); Y = (a × b)/ c; Y = (a + b) c и т.д. Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции (см. рис. 5.2) можно применять такие детерминированные модели, как: ВП = ЧР × ГВ; ВП = ЧР ×Д ×ДВ; ВП = ЧР × Д × П × ЧВ. Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Степень детализации и расширения модели зависит от цели исследования, а также от возможностей детализации и формализации показателей в пределах установленных правил. Аналогичным образом осуществляется моделирование аддитивных факторных систем за счет расчленения одного или нескольких факторных показателей на составные элементы. Как известно, объем реализации продукции равен VРП = VВП – Онп, где VВП — объем выпуска продукции; Онп — остатки нереализованной продукции. Часть нереализованной продукции может находиться на складах предприятия (Оскл), а часть может быть отгружена покупателям, но еще не оплачена (Оотг) Тогда приведенную исходную модель можно записать следующим образом: VРП = VВП – Оскл – Оотг, К классу кратных моделей применяют следующие способы их преобразования: удлинения, формального разложения, расширения и сокращения. Первый метод предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы продукции можно представить в качестве функции двух факторов: изменения суммы затрат (З)и объема выпуска продукции(VВП). Исходная модель этой факторной системы будет иметь вид С = З / VВП. Если общую сумму затрат (З)заменить отдельными их элементами, такими, как заработная плата (ЗП), сырье и материалы (СМ), амортизация основных средств (А), накладные расходы (HP)и др., то детерминированная факторная модель будет иметь вид аддитивной модели с новым набором факторов: С = где Х 1 — трудоемкость продукции; Х 2— материалоемкость продукции; Х 3 — фондоемкость продукции; Х 4 — уровень накладных расходов. Способ формального разложения факторной системы предусматривает удлинение знаменателя исходной факторной модели путем замены одного или нескольких факторов на сумму или произведение однородных показателей. Если B = L + M + N + P, то Y = В результате получили конечную модель кратно-аддитивного вида с новым набором факторов. На практике такое разложение встречается довольно часто. Например, при анализе показателя рентабельности производства (R) R = где П — сумма прибыли от реализации продукции; З — сумма затрат на производство и реализацию продукции. Если сумму затрат заменить на отдельные ее элементы, конечная модель в результате преобразования приобретет следующий вид: R = Себестоимость одного тонно-километра зависит от суммы затрат на содержание и эксплуатацию автомобиля (З) и от его среднегодовой выработки (ГВ). Исходная модель этой системы будет иметь вид: Сткм = З / ГВ. Учитывая, что среднегодовая выработка машины в свою очередь зависит от количества отработанных дней одним автомобилем за год (Д) продолжительности смены (Я) и среднечасовой выработки (ЧВ) мы можем значительно удлинить эту модель и разложить прирост себестоимости на большее количество факторов: Сткм = Метод расширения предусматривает расширение исходной факторной модели за счет умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в исходную модель Y = A / B ввести новый показатель С, то модель примет вид Y = В результате получилась конечная мультипликативная модель в виде произведения нового набора факторов. Этот способ моделирования очень широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом: ГВ = ВП / ЧР. Если ввести такой показатель, как количество отработанных дней всеми работниками (D), то получим следующую модель годовой выработки: ГВ = где ДВ — среднедневная выработка; Д — количество отработанных дней одним работником. После введения показателя количества отработанных часов всеми работниками (Т) получим модель с новым набором факторов: среднечасовой выработки (ЧВ), количества отработанных дней одним работником (Д) и продолжительности рабочего дня (П). ГВ = Способ сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель: Y = В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов. И снова практический пример. Как известно, рентабельность операционного капитала рассчитывается делением суммы прибыли от реализации продукции (П) на среднегодовую стоимость основного и оборотного капитала предприятия (KL): R = П / KL. Если числитель и знаменатель разделим на объем реализации продукции (товарооборот), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции: R = И еще один пример. Фондоотдача (ФО)определяется отношением валовой (ВП)или товарной продукции (ТП) к среднегодовой стоимости основных производственных фондов (ОПФ): ФО = Разделив числитель и знаменатель на среднегодовое количество рабочих (ЧР), получим более содержательную кратную модель с другими факторными показателями: среднегодовой выработки продукции одним рабочим (ГВ), характеризующей уровень производительности труда, и фондовооруженности труда (Фв) ФО = Необходимо заметить, что на практике для преобразования одной и той же модели может быть последовательно использовано несколько методов. Например, процесс создания факторной модели рентабельности совокупного капитала (RKL)можно представить следующим образом: RKL = где БП — сумма балансовой (валовой) прибыли за отчетный период; KL — среднегодовая сумма совокупного капитала; Прп — прибыль от реализации продукции (услуг); ВФР — внереализационные финансовые результаты; В — выручка от реализации продукции (услуг); VРПi — объем реализации продукции вида в натуральном выражении; Цi — отпускные цены на i -йвид продукции; Ci — себестоимость единицы i -го вида продукции; Коб — коэффициент оборачиваемости совокупного капитала за отчетный период (отношение выручки к среднегодовой сумме капитала). В данном случае для преобразования исходной факторной модели, построенной на математических зависимостях, использованы способы удлинения и расширения. В результате получилась более содержательная модель мультипликативно-аддитивно-кратного вида, которая имеет большую познавательную ценность, поскольку учитывает причинно-следственные связи между показателями. Данная модель позволяет исследовать, как влияют на доходность капитала объем продаж, отпускные цены, себестоимость реализованной продукции, внереализационные финансовые результаты, а также скорость обращения капитала. Таким образом, результативные показатели могут быть разложены на составные элементы (факторы) различными способами и представлены в виде различных типов детерминированных моделей. Выбор способа моделирования зависит от объекта исследования, от поставленной цели, а также от профессиональных знаний и навыков исследователя. Процесс моделирования факторных систем — очень сложный и ответственный момент в АХД. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 568; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |



 Себестоимость единицы продукции
Себестоимость единицы продукции


 культур
культур


 = X 1 + X 2 +X 3 +…+Xn.
= X 1 + X 2 +X 3 +…+Xn. = X 1 × X 2 × X 3 ×…× Xn.
= X 1 × X 2 × X 3 ×…× Xn.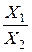
 +
+  +
+ 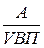 +
+ 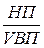 = Х 1 + Х 2 + Х 3 + Х 4.
= Х 1 + Х 2 + Х 3 + Х 4.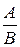 =
= 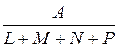 .
.

 =
=  .
. =
= 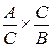 = X 1 × X 2.
= X 1 × X 2. =
=  = ДВ × Д,
= ДВ × Д, =
=  = ЧВ × Д × П.
= ЧВ × Д × П. =
= 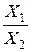 .
. =
=  =
=  .
. .
. =
=  .
. =
=  =
= 



