
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение направления взаимосвязиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кроме формы взаимосвязи, корреляционное поле позволяет определить направление взаимосвязи (рис. 15): если между исследуемыми признаками наблюдается прямо пропорциональная зависимость, т. е. с увеличением одного показателя увеличивается и другой, то взаимосвязь положительная; если же зависимость обратно пропорциональная, т. е. с увеличением одного показателя другой уменьшается, то имеет место отрицательная взаимосвязь. В первом случае при расчёте коэффициент корреляции получается со знаком «+», а во втором случае – со знаком «-».
Рис 15. Направление связи
Определение степени или тесноты взаимосвязи
Анализ корреляционного поля позволяет определить не только форму и направление взаимосвязи, но и степень зависимости, или тесноту (силу) связи. Ниже приводятся графики при различной степени связи с соответствующими им коэффициентами корреляции при положительной зависимости (рис. 16а) и при отрицательной зависимости (рис. 16б). Как видно из рисунка, чем ближе корреляционное поле к прямой, тем больше по модулю коэффициент корреляции, значит, тем сильнее зависимость между исследуемыми результатами; а чем ближе форма корреляционного поля к окружности, тем меньше по модулю коэффициент корреляции и тем слабее зависимость между исследуемыми результатами. По приведённым графикам видно, что в случае, когда коэффициент корреляции равен +1 или -1, то наблюдается функциональная взаимосвязь, т. к. значению одного показателя соответствует только одно значение другого и поэтому никакой вариации на корреляционном поле не наблюдается. Причём, если в первом ряду представлены виды прямо пропорциональной зависимости корреляционного поля, когда увеличение одного показателя связано с увеличением другого; то во втором ряду представлены виды обратно пропорциональной зависимости корреляционного поля, когда увеличение одного показателя связано с уменьшением другого (в среднем). Таким образом, по виду корреляционного поля можно судить о степени взаимосвязи между исследуемыми показателями и сделать предварительный вывод, который затем подтверждается расчётом коэффициента корреляции, приведённым ниже.
а)
б) Рис 16. Степень связи
Парный линейный коэффициент корреляции Бравэ-Пирсона (r). Коэффициент детерминации (D) Парный линейный коэффициент корреляции Бравэ-Пирсона вычисляется в том случае, когда между показателями исследуемых выборок (Х i и У i) существует линейная связь. Если Х и У независимые случайные величины, то коэффициент корреляции равен 0. Заметим, что обратное утверждение неверно. Если r = 0, то между изучаемыми признаками нет линейной корреляционной зависимости, но это условие не исключает существования какого-либо другого вида корреляционной зависимости (параболической, показательной и др.) Одна из формул для расчета коэффициента корреляции Бравэ-Пирсона:
где Xi, Yi - показатели первой и второй выборок соответственно;
n - объем каждой выборки. Абсолютная величина коэффициента корреляции не превосходит единицы: Коэффициент корреляции характеризует степень зависимости, или тесноту (силу) зависимости между Х и У, чем больше Принято считать, если: · коэффициент корреляции равен 1, то между исследуемыми признаками наблюдается функциональная связь; · изменяется от ±0,9 до ± 0,7 - сильная статистическая связь; · изменяется от ±0,69 до ±0,5 - средняя статистическая связь; · изменяется от ± 0,49 до ±0,2 - слабая статистическая связь; · коэффициент корреляции равен нулю - то между изучаемыми признаками нет линейной корреляционной зависимости. Таким образом, коэффициент корреляции Бравэ-Пирсона r используется только при наличии линейной взаимосвязи между исследуемыми признаками. Существует несколько видов коэффициентов корреляции: парный линейный коэффициент корреляции Бравэ - Пирсона r, ранговый коэффициент корреляции Спирмэна r, тетрахорический коэффициент сопряженности Т, коэффициент множественной корреляции r xyz, коэффициент частной корреляции r xyz. После вычисления любого из перечисленных выше коэффициентов корреляции, необходимо рассчитать его достоверность с использованием критерия Стьюдента. В некоторых случаях тесноту связи случайных величин характеризуют коэффициентом детерминации D, равным:
Коэффициент детерминации показывает, какой процент взаимосвязи результатов двух выборок объясняется их взаимовлиянием. Остальная часть (100 - D)% объясняется влиянием других неучтённых факторов.
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 1100; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.38.170 (0.006 с.) |




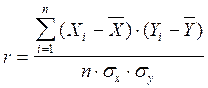
 - средние арифметические значения первой и второй выборок соответственно;
- средние арифметические значения первой и второй выборок соответственно; - стандартные отклонения первой и второй выборок соответственно;
- стандартные отклонения первой и второй выборок соответственно; < 1.
< 1.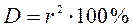 .
.


