
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные статистические характеристики ряда измеренийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
К основным статистическим характеристикам ряда измерений (вариационного ряда) относятся характеристики положения (средние характеристики, или центральная тенденция выборки); характеристики рассеяния (вариации, или колеблемости) и х арактеристики формы распределения. К характеристикам положения относятся среднее арифметическое значение (среднее значение), мода и медиана. К характеристикам рассеяния (вариации, или колеблемости) относятся: размах вариации, дисперсия, среднее квадратическое (стандартное) отклонение, ошибка средней арифметической (ошибка средней), коэффициент вариации и др. К характеристикам формы относятся коэффициент асимметрии, мера скошенности и эксцесс. Далее приводятся формулы для расчёта основных статистических характеристик, причём предлагаются расчётные формулы как для несгруппированных данных, так и для данных, сгруппированных в интервалы.
Характеристики положения Среднее арифметическое значение Среднее арифметическое значение – одна из основных характеристик выборки. Она, как и другие числовые характеристики выборки, может вычисляться как по необработанным первичным данным, так и по результатам группировки этих данных. Точность вычисления по необработанным данным выше, но процесс вычисления оказывается трудоёмким при большом объёме выборки. Для несгруппированных данных среднее арифметическое определяется по формуле:
где n - объем выборки, х 1, х 2,... х n - результаты измерений. Для сгруппированных данных:
где n - объем выборки, k – число интервалов группировки, ni – частоты интервалов, xi – срединные значения интервалов.
Мода Определение 1. Мода - наиболее часто встречающаяся величина в данных выборки. Обозначается Мо и определяетсяпо формуле:
где Определение 2. Модой Мо дискретной случайной величины называется наиболее вероятное её значение. Геометрически моду можно интерпретировать как абсциссу точки максимума кривой распределения. Бывают двухмодальные и многомодальные распределения. Встречаются распределения, которые имеют минимум, но не имеют максимума. Такие распределения называются антимодальными. Определение. Модальным интервалом называется интервал группировки с наибольшей частотой. Медиана Определение. Медиана - результат измерения, который находится в середине ранжированного ряда, иначе говоря, медианой называется значение признака Х, когда одна половина значений экспериментальных данных меньше её, а вторая половина – больше, обозначается Ме. Когда объем выборки n - четное число, т. е. результатов измерений четное количество, то для определения медианы рассчитывается среднее значение двух показателей выборки, находящихся в середине ранжированного ряда. Для данных, сгруппированных в интервалы, медиану определяют по формуле:
где Определение. Медианным интервалом называется тот интервал, в котором накопленная частота впервые окажется больше половины объёма выборки (n/ 2) или накопленная частость окажется больше 0,5. Численные значения среднего, моды и медианы отличаются, когда имеет место несимметричная форма эмпирического распределения.
Характеристики рассеяния результатов измерений Для математико-статистического анализа результатов выборки знать только характеристики положения недостаточно. Одна и та же величина среднего значения может характеризовать совершенно различные выборки. Поэтому кроме них в статистике рассматривают также характеристики рассеяния (вариации, или колеблемости) результатов.
Размах вариации Определение. Размахом вариации называется разница между наибольшим и наименьшим результатами выборки, обозначается R и определяется R = X max - X min. Информативность этого показателя невелика, хотя при малых объёмах выборки по размаху легко оценить разницу между лучшим и худшим результатами спортсменов. Дисперсия Определение. Дисперсией называется средний квадрат отклонения значений признака от среднего арифметического. Для несгруппированных данных дисперсия определяется по формуле s2 =
где Хi – значение признака, Для данных, сгруппированных в интервалы, дисперсия определяется по формуле
где хi – среднее значение i интервала группировки, ni – частоты интервалов. Для упрощения расчётов и во избежание погрешностей вычисления при округлении результатов (особенно при увеличении объёма выборки) используются также другие формулы для определения дисперсии. Если среднее арифметическое уже вычислено, то для несгруппированных данных используется следующая формула:
s2 = для сгруппированных данных:
Эти формулы получаются из предыдущих раскрытием квадрата разности под знаком суммы. В тех случаях, когда среднее арифметическое и дисперсия вычисляются одновременно, используются формулы: для несгруппированных данных: s2 = для сгруппированных данных:
3. Среднее квадратическое (стандартное) отклонение Определение. Среднее квадратическое (стандартное) отклонение характеризует степень отклонения результатов от среднего значения в абсолютных единицах, т. к. в отличие от дисперсии имеет те же единицы измерения, что и результаты измерения. Иначе говоря, стандартное отклонение показывает плотность распределения результатов в группе около среднего значения, или однородность группы. Для несгруппированных данных стандартное отклонение можно определить по формулам
s =
s =
Для данных, сгруппированных в интервалы, стандартное отклонение определяется по формулам:
|
||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 5180; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.011 с.) |

 ,
, ,
,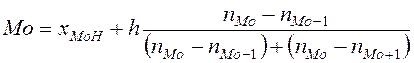 ,
, - нижняя граница модального интервала,
- нижняя граница модального интервала,  - ширина интервала группировки,
- ширина интервала группировки, 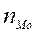 - частота модального интервала,
- частота модального интервала,  - частота интервала, предшествующего модальному,
- частота интервала, предшествующего модальному,  - частота интервала, последующего за модальным.
- частота интервала, последующего за модальным.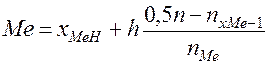 ,
, - нижняя граница медианного интервала;
- нижняя граница медианного интервала;  ширина интервала группировки, 0,5 n – половина объёма выборки,
ширина интервала группировки, 0,5 n – половина объёма выборки,  - частота медианного интервала,
- частота медианного интервала,  - накопленная частота интервала, предшествующего медианному.
- накопленная частота интервала, предшествующего медианному. , (1)
, (1) - среднее арифметическое.
- среднее арифметическое. ,
,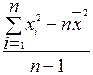 ,
,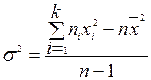 .
. ,
, .
.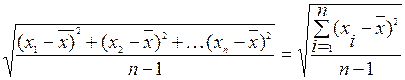 ,
,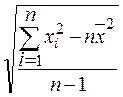 или s =
или s =  .
.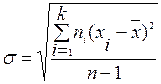 ,
,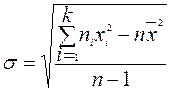 или
или  .
.


