
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка достоверности статистических показателейСодержание книги
Поиск на нашем сайте
Часто в спорте стоит следующая задача: как по результатам измерений сделать какой-то обобщающий вывод. Пример1. Группу борцов тестировали в начале и конце тренировочного занятия по следующему тесту: сделать 8 бросков в максимальном темпе с измерением времени выполнения (с). начало тренировки: конец тренировки: Влияет ли тренировка на изменение времени выполнения бросков. Влияет ли нагрузка на изменение скоростных качеств? Пример 2. Измеряли массу тела у юношей (10 спортсменов) и девушек (10 спортсменов), специализирующихся в самбо.
Различаются ли массы тела юношей от массы тела девушек. Для ответа на вопросы: - как сравнить средние результаты различных групп; - как оценить влияние тренировочного занятия на тот или иной показатель; - как определить (предсказать) интервал, в котором лежат исследуемые показатели; необходимо использовать приемы проверки статистических гипотез.
Статистические гипотезы
Гипотеза - научное предположение. Статистическая гипотеза - предположение о характеристиках, которые доказываются методами математической статистики. Статистическую гипотезу обычно обозначают буквой Н (от греческого Hipotes). Гипотеза называется нулевой (Но), если отсутствует различие между сравниваемыми выборками ( Противоположной (альтернативной или единичной) гипотезой (Н1) будет предположение о том, что
Виды статистических гипотез
· Гипотеза о доверительном интервале. · Гипотеза о достоверности различий средних арифметических: -связанных выборок; -несвязанных выборок. · Гипотеза о достоверности различий дисперсий. · Гипотеза о достоверности коэффициента корреляции. При проверке статистических гипотез решение никогда не принимается с уверенностью, т.е. всегда есть вероятность принять неправильное решение. Уровень значимости - вероятность появления ошибки при выборе гипотезы. Следует отметить, что любая гипотеза должна формулироваться, а уровень значимости В таблице приведены значения вероятности события при различных значениях ошибки предположения.
Уровень значимости и вероятность события Таблица 5
Уровень значимости 0,05 означает, что ошибочное значение может встретиться, например, в 5 наблюдениях из 100. Обычно в научных исследованиях в области физической культуры и спорта считается достаточной доверительная вероятность 0,95 (95%), тогда уровень значимости Только в тех случаях, когда выводы, сделанные в конкретном исследовании, связаны с большой ответственностью или же уточняются результаты предыдущих исследований, применяются высокие уровни доверительной вероятности: 99 или 99,9% (уровень значимости 0,01 (1 %) или 0,001 (0,1 %) соответственно). Доверительная вероятность – вероятность, признанная достаточной для того, чтобы уверенно судить о генеральных параметрах на основании выборочных характеристик. Основные этапы проверки статистической гипотезы. 1. Формулировка гипотезы, которую в дальнейшем необходимо принять или отклонить. Но: H1: 2. Определить расчетное значение критерия, то есть некоторой величины по определенной заданной формуле. Критерий – правило, с помощью которого подтверждается или отвергается та или иная гипотеза.
3. Определить табличные критические значения (по таблице, см. приложение). tтабл., Fтабл. Для этого необходимо знать: n - число степеней свободы и 4. Сравнить значения расчетного коэффициента с табличным: tpacч.ó tтабл. Fpacч. ó Fтабл. 5. Сделать вывод. Статистическая гипотеза принимается или отвергается. а) если tpacч. £ tтабл. ( если tpacч.> tтабл. - нулевая гипотеза отвергается, тем самым утверждается, что средние арифметические двух выборок не равны. б) если Fрасч.<Fтабл., то нулевая гипотеза о равенстве дисперсий двух выборок (Но: если Fpacч ³ Fтабл., то нулевая гипотеза отклоняется с вероятностью q =1-
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-19; просмотров: 603; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.7.187 (0.009 с.) |





 ).
).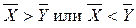 .
. задаётся исследователем всегда до получения экспериментальных данных, по которым эта гипотеза будет проверяться.
задаётся исследователем всегда до получения экспериментальных данных, по которым эта гипотеза будет проверяться.
 (r-коэффициент корреляции)
(r-коэффициент корреляции)
 - уровень значимости.
- уровень значимости. ) принимается с вероятностью q =1-
) принимается с вероятностью q =1-  ) принимается с вероятностью q =1-
) принимается с вероятностью q =1- 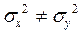 ). Из двух выборок более однородна будет та, у которой значение дисперсии меньше.
). Из двух выборок более однородна будет та, у которой значение дисперсии меньше.


