
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уровень значимости и мощность критерия. Ошибки первого и второго рода.Содержание книги
Поиск на нашем сайте
Проверяя гипотезы с помощью статистического критерия, может возникнуть одна из четырех ситуаций: 1) гипотеза H0 истинна (и поэтому H1 – ложна) и предпринимается действие А; 2) гипотеза H1 истинна (и поэтому H0 – ложна) и предпринимается действие А; 3)) гипотеза H0 истинна (и поэтому H1 – ложна) и предпринимается действие В; 4) гипотеза H1 истинна (и поэтому H0 – ложна) и предпринимается действие В. В ситуациях 2 и 3 получается ошибка. Существует 2 типа ошибок. Ошибка, состоящая в принятии гипотезы H0, когда она ложна (ошибка второго рода), качественно отличается от ошибки, состоящей в отвержении H0, когда она истинна (ошибка первого рода). При этом числа αi = αi(δ) = Pi(δ(X)≠ Hi), характеризующие вероятность отвержения гипотезы Hi, когда она верна, называют вероятностями ошибок (i+1)-го рода критерия δ. Набором вероятностей αi(δ) ошибочных решений характеризуется кач-вом критерия δ. Правильное решение также может быть принято двумя способами (ситуации 1 и 4): когда гипотеза H0 принимается, ибо она верна, и когда гипотеза H0 отвергается, ибо она ложна. В ситуации 1 не совершается ошибка первого рода, в ситуации 4 – второго рода. Уровень значимости критерия не меняет степени риска, связанного с возможностью ошибки второго рода, т.е. с принятием неверной гипотезы. И при данном уровне значимости можно по-разному определить критическую область. Как правило, ее определяют так, чтобы мощность критерия 1 – α1(δ) была возможно большей: P (X
Критерий согласия. Критерий согласия Пирсона основан на выборе определенной меры расхождения между теоретическим и эмпирическим (полученным из эксперимента) распределениями. Причем задачу проверки согласованности теории с опытными данными можно сформулировать в следующем виде: имеется выборка х1, х2, …, хn наблюденных значений некоторой СВ Х. Требуется определить, что выборочное распределение принадлежит определенному распределению (нормальному, биномиальному, показательному и т.д.) – гипотеза Н0 против альтернативной гипотезы Н1 – распределение не принадлежит выбранному распределению. Допустим вначале, что гипотеза Н0 полностью определяет вид функции Р, и вероятность P(xj
|
|||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 465; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.87.240 (0.007 с.) |

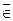 ] x1; x2[|H1) = max. Мощностью критерия δ называется вероятность 1 – α1(δ) несовершения ошибки второго рода. Чем больше мощность критерия, тем меньше вероятность принятия неверной гипотезы.
] x1; x2[|H1) = max. Мощностью критерия δ называется вероятность 1 – α1(δ) несовершения ошибки второго рода. Чем больше мощность критерия, тем меньше вероятность принятия неверной гипотезы. Si) может быть вычислена для любого заданного мн-ва S1, S2, …, Sk – это либо интервалы для непрерывной СВ, либо группы отдельных значений дискретной СВ, не имеющие общих точек. Пусть pi = P(xj
Si) может быть вычислена для любого заданного мн-ва S1, S2, …, Sk – это либо интервалы для непрерывной СВ, либо группы отдельных значений дискретной СВ, не имеющие общих точек. Пусть pi = P(xj  =1, причем все pi>0, i =
=1, причем все pi>0, i =  . Соответствующие групповые частоты в выборке m1, m2, …, mk, т.е. mi – это число значений СВ Х из выборки, попавших в Si. Ясно, что
. Соответствующие групповые частоты в выборке m1, m2, …, mk, т.е. mi – это число значений СВ Х из выборки, попавших в Si. Ясно, что 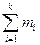 =n. Если проверяемая гипотеза Н0 верна, то распределение выборки можно рассматривать как статистический аналог для генерального распределения, определяемого функцией р(х). Это значит, что mi представляет собой частоту появления события с вероятностью pi = P(Si) в нашей последовательности из n наблюдений. Следовательно, любое мн-во Si имеет в первом распределении относительные частоты mi/n, а во втором – вероятности pi. Тогда, согласно методу наименьших квадратов, за меру расхождения между распределением выборки и теоретическим распределением примем величину
=n. Если проверяемая гипотеза Н0 верна, то распределение выборки можно рассматривать как статистический аналог для генерального распределения, определяемого функцией р(х). Это значит, что mi представляет собой частоту появления события с вероятностью pi = P(Si) в нашей последовательности из n наблюдений. Следовательно, любое мн-во Si имеет в первом распределении относительные частоты mi/n, а во втором – вероятности pi. Тогда, согласно методу наименьших квадратов, за меру расхождения между распределением выборки и теоретическим распределением примем величину  Ci(mi/n - pi)2, где Ci – произвольный коэффициент. Пирсон доказал, что если Ci = n/ pi, то получится мера расхождения вида χ2 =
Ci(mi/n - pi)2, где Ci – произвольный коэффициент. Пирсон доказал, что если Ci = n/ pi, то получится мера расхождения вида χ2 = 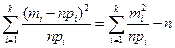 , такая, что при увеличении объема выборки выборочное рапределение величины χ2 стремится к предельному распределению χ2 с υ = κ – r – 1 степенями свободы (к – число интервалов или групп, на кторые разбито все мн-во наблюденных данных, r – число параметров гипотетического распределения вероятностей Р, оцениваемых по данным выборки). Это утверждение следует из того, что если гипотеза Н0 верна, то совместным распределением групповых частот mi, i =
, такая, что при увеличении объема выборки выборочное рапределение величины χ2 стремится к предельному распределению χ2 с υ = κ – r – 1 степенями свободы (к – число интервалов или групп, на кторые разбито все мн-во наблюденных данных, r – число параметров гипотетического распределения вероятностей Р, оцениваемых по данным выборки). Это утверждение следует из того, что если гипотеза Н0 верна, то совместным распределением групповых частот mi, i = 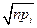 нормально распределены, а их сумма квадратов χ2 =
нормально распределены, а их сумма квадратов χ2 =  имеет распределение χ2 с υ = κ – r – 1 степенями свободы. Для того, чтобы величина критерия приближенно имела χ2-распределение, теоретические частоты npi должны быть не слишком малыми.
имеет распределение χ2 с υ = κ – r – 1 степенями свободы. Для того, чтобы величина критерия приближенно имела χ2-распределение, теоретические частоты npi должны быть не слишком малыми.


