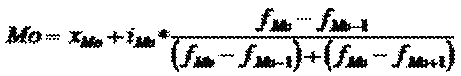Типическая, серийная, собственно-случайная и механическая выборки

 

Типическая выборка

Типическую выборку применяют для отбора единиц из неоднородной совокупности. Она используется тогда, когда все единицы генеральной совокупности можно разбить на несколько качественно однотипных групп по признакам, которые влияют на изучаемые показатели.

При анализе предприятий такими группами могут быть: отрасль, формы собственности, специфика работы и т. д. Затем из каждой типической группы механической или собственно-случайной выборкой производят индивидуальный отбор единиц в выборочную совокупность.

Часто типическая выборка применяется при анализе сложных статистических совокупностей (например, производительность труда рабочих организации, представленных отдельными группами по квалификации). Такой вид выборки дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность.
При расчете средней ошибки типической выборки в качестве показателя вариации берут среднюю из внутригрупповых дисперсий.

 

Серийная (гнездовая) выборка

В серийной выборке происходит случайный отбор из генеральной совокупности не отдельных единиц, а их равновеликих групп, с тем чтобы в этих группах все единицы были подвергнуты наблюдению.

Серийная выборка определена тем, что многие товары для их транспортировки, хранения или продажи упаковываются, следовательно при контроле качества упакованного товара рациональнее провести проверку несколько серий упаковок, чем из всех упаковок отбирать необходимое количество товара.

В связи с тем, что внутри групп (или серий) анализируются все единицы, средняя ошибка выборки при отборе равновеликих серий зависит только от межгрупповой (или межсерийной) дисперсии.

 

Механическая выборка

Механическая выборка характеризуется тем, что отбор единиц в выборочную совокупность из генеральной, разбитую по нейтральному признаку на равные интервалы, в задачах статистики проводится так, что из каждой такой группы в выборку отбирается лишь одна единица.

Для того, чтобы избежать систематической ошибки, отбирается единица, которая находится в середине каждой группы.

При организации механического отбора единицы совокупности заранее располагают в определенном порядке и далее отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.

При анализе достаточно большой совокупности механический отбор по точности результатов близок к случайному. Поэтому для определения средней ошибки механической выборки пользуются формулами собственно-случайной бесповторной выборки.

 

Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или невключение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.

 

Структурные средние

 

Характеристиками структуры совокупности являются следующие структурные средние:

1. Мода (Mo) – величина признака, наиболее часто встречающаяся в совокупности, т.е. имеющая наибольшую численность в ряду распределения.

а) В дискретном ряду распределения мода определяется визуально.

б) В интервальном ряду распределения визуально можно определить только интервал, в котором заключена мода, который называется модальным интервалом. Мода будет равна:

2. Медиана (Me) – значение признака, приходящееся на середину ранжированного ряда, т.е. делящее ряд распределения на две равные части.

а) В дискретном ряду распределения определяется номер медианы по формуле:

Номер медианы показывает то значение показателя, которое и является медианой.

б) В интервальном ряду распределения медиана рассчитывается по следующей формуле: