
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение необходимой численности выборки.Содержание книги
Поиск на нашем сайте
При проведении выборочного наблюдения важно определить численность выборочной совокупности, которая с определённой вероятностью обеспечит заданную точность результатов. Необходимые формулы можно получить из формул ошибок выборки: 1) д/повторного отбора: ОШИБКА ВЫБОРКИ ПРИ ТИПИЧЕСКОМ ОТБОРЕ. При типической выборке выбираются единицы из групп ГС, выделенные по определённому признаку, поэтому ошибка выборки будет зависеть от вариации признака внутри каждой группы. Эта внутригрупповая вариация измеряется средней из групповых дисперсий. Поэтому при типической выборке в формулах ошибки выборки вместо общей дисперсии σ2 следует учитывать ОШИБКА ВЫБОРКИ ПРИ СЕРИЙНОМ ОТБОРЕ. При серийном отборе наиболее часто выбирают равновеликие серии. В отобранных сериях производится сплошное наблюдение единиц, поэтому ошибка выборки зависит от числа отобранных серий и от вариаций средних внутри серий, кот. измер-ся межсерийной дисперсией. Если общее число серий ГС R, а число отобранных серий r, то имеем: 1) д/повторного отбора: ОШИБКА ВЫБОРКИ ПРИ КОМБИНИРОВАННОЙ ВЫБОРКЕ. При комбинированной выборке выборочная совокупность формируется в результате ступенчатого отбора. Например, д/изучения успеваемости студентов факультета сначала отбирают группы, а затем в каждой группе случайно или механически отбирают число студентов. Поэтому общая ошибка выборки складывается из ошибок на каждой ступени и определяется как корень квадратный из суммы ошибок соответствующих выборок. Например, при комбинировании серийной выборки ошибка будет определятся по формуле: ОШИБКА ВЫБОРКИ ПРИ МАЛОЙ ВЫБОРКЕ.
( РАСПРОСТРАНЕНИЕ РЕЗУЛЬТАТОВ ВЫБОРКИ НА ГЕНЕРАЛЬНУЮ СОВОКУПНОСТЬ. Конечной целью выборки явл-ся распространение результатов выборки на ГС. Существует 2 способа: 1. способ прямого пересечения; среднее значение ве-ны признака выборочной совокупности умножается на число единиц ГС (напр, средняя зарплата по выборке на число всех рабочих); 2. способ коэффициентов; применяется в том случае. Когда выборочное наблюдение проводится д/уточнения результатов сплошного; отношение ве-ны признака по выборке к ве-не сплошного наблюдения даёт поправочный коэффициент, на который корректируют данное сплошное наблюдение.
ТЕМА 8. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ КОРРЕЛЯЦИОННЫХ СВЯЗЕЙ. ПОНЯТИЕ И ЗАДАЧИ КОРРЕЛЯЦИИ Различают связи: 1) функциональная; связь, при которой каждому значению факторного признака соответствует 1 или несколько строго определённых значений результативного признака (напр, Sкруга=ПR2); такие связи характерны д/естественных наук, они являются точными и полными, обнаруживаются на небольшом числе единиц; 2) корреляционная связь; связь, при которой каждому значению факторного признака соответствует среднее значение результативного признака при большом числе наблюдений; эти связи могут быть приближённые, неполные. Корреляция – соотношение, соответствие; отношение связи между переменными ве-нами. Выделяют корреляции: 1) парная: y=f (a), y=f(b) (влияние отдельных факторов на изучаемый); 2) множественная: y = f (a,b,c) (влияние нескольких факторов на изучаемый). В зависимости от направления действия связи бывают: прямая (направления изменения признака совпадают – оба ↑ или ↓, в противном случае связь обратная. При решении корреляционных задач мы заменяем корреляционные связи функциями, выражая их соответствующими уравнениями. По аналитическому выражению связи могут быть: прямолинейными (описыв-ся уравнением прямой), криволинейные ( описыв-ся уравнением параболы, гиперболы…). Требования при изучении корреляц-ой связи: 1) однородность совокупности и её колич-ой оценки; можно д/этого применить коэфф-т вариации; 2) должно быть достаточно большое число наблюдений, → происходит взаимопогошение случайных факторов; 3) ограничение числа факторов, которые должны быть независимо друг от друга; 4) должен быть нормальный хар-р распределения исследуемых признаков; 5) факторы должны иметь количественное выражение, иначе нельзя будет построить модель корреляционной зависимости; 6) число единиц, при изучении корреляционной связи должно быть в 5-6 раз больше, чем признаков. При изучении коррел-ой связи нужно решить следующие задачи:1) убедиться, что связь между признаками существует; 2) измерить степень тесноты связи между признаками; 3) опред-ть формулу связи, т.е. аналитическое выражение; 4) выявить влияние отдельных факторов на изучаемый. ОПРЕДЕЛЕНИЕ ФОРМЫ СВЯЗИ. Д/определения ха-ра и направления связи применяется ряд приёмов: 1) метод сопоставления двух параллельных рядов: строится ранжированный ряд по факторному признаку, а результативный записывается соотв-но своим значениям, полученные ряды сравниваются; недостаток приёма – при большом числе единиц получается труднообозримый ряд, трудно обнаружить связь; 2) формы связи можно обнаружить графически;3) на практике изучение связей между признаками часто базируется на большом числе наблюдений, мат-лы которых группируются по 2ум взаимосвязанным признакам; результате группировки оформляются в виде корреляционной таблицы или решётки (таблица в подлежащем которой располагается значение факторного признака, а в сказуемом – результативного). Чаще всего строятся интервальные ряды. Ве-на интервала опр-ся по формуле: (хmax – хmin) /n, (n=1+3,322 lgN). На основании Корреляционной решётки можно сделать выводы: а) сравнивая значения между признаками можно сделать вывод о связи между признаками; б) если не рассчитывать средние ве-ны, то по расположению единиц в корреляционной решётке можно сделать вывод о ха-ре, направлении и тесноте связи: 1) если частоты располагаются от верхнего левого угла к нижнему правому → связь прямая, если наоборот → связь обратная; 2) чем уже расположена полоса частот, чем связь теснее» в) если частоты располагаются по прямой → связь прямолинейна, по кривой → криволинейна; г) в случае, если все клетки корреляционной решётки окажутся заполненными, нужно установить как расположена основная масса частот
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 332; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.92.58 (0.009 с.) |

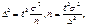 д/альтернативных признаков:
д/альтернативных признаков:  ; д/бесповторного отбора:
; д/бесповторного отбора: 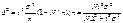 , д/альтернативных признаков:
, д/альтернативных признаков: 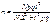 . Внутригруппировочная вариация измеряется из группировочных дисперсий, поэтому при типичной выборке в формулах ошибки выборки вместо общей σ2 следует учитывать
. Внутригруппировочная вариация измеряется из группировочных дисперсий, поэтому при типичной выборке в формулах ошибки выборки вместо общей σ2 следует учитывать 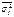 , если речь идёт о средней и
, если речь идёт о средней и 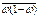 , если речь идёт о доле
, если речь идёт о доле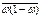 , если речь идёт о доле. Таким образом имеем: при повторном отборе: д/средней
, если речь идёт о доле. Таким образом имеем: при повторном отборе: д/средней  , д/доли
, д/доли  ; при бесповторном отборе: д/средней
; при бесповторном отборе: д/средней  , д/доли
, д/доли  ,
,  . По формулам сначала определяется общая численность выборки, а затем объём выборки из каждой группы, пропорционально их удельному весу.
. По формулам сначала определяется общая численность выборки, а затем объём выборки из каждой группы, пропорционально их удельному весу. 2)д/бесповторного отбора:
2)д/бесповторного отбора: 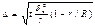

 зачастую на практике применяются малые выборки (n≤30). При малых выборках µ имеет распределение Стьюдента и равно:
зачастую на практике применяются малые выборки (n≤30). При малых выборках µ имеет распределение Стьюдента и равно: 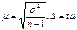 , где
, где 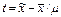
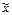 -выборочное,
-выборочное, 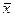 -генеральное). Стьюдент доказал, что в случае малой выборки действует особый закон распределения вероятности, здесь ∆ зависит от t и n. По мере роста n распределение в малых выборках стремится к нормальному.
-генеральное). Стьюдент доказал, что в случае малой выборки действует особый закон распределения вероятности, здесь ∆ зависит от t и n. По мере роста n распределение в малых выборках стремится к нормальному.


