
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Единая система учёта и статистики рбСодержание книги
Поиск на нашем сайте
ПРЕДМЕТ СТАТИСТИКИ Считают,что понятие ст-ка походит от лат.слова «статус»,что означает положение, состояние, явление или стато(гос-во).Первоначально государствоведение. В наст. Время ст-ка употр. В 3-х значениях: 1)Это практическая деятельность людей осущ-их сбор,обработку и анализ данных о соц.-эк. Развитии страны,отдельных отраслей и п/п. 2)Это наука, разрабатывающая теорию и методы статич. практики. Они взаимно обогащают др. друга.Практика применяет правила, выбранные наукой, а наука обобщает опыт практики. 3)Данные отчётности п/п,орг-ций,отраслей и всего хоз-ва страны. Статистика -общ.наука,к-ая занимается сбором и обобщением данных о развитии общества. Ст-ка как наука стала развиваться с сер. 17в. по 2-ум напрвлениям: 1.описательному 2.мат-кому Описательная ст-ка – это описание гос.достопримечательностей(терр.,гос.устр-ва,населения,религии и тд).Они не пользовались числовыми данными и отсутств.анализ взаимосвязей обществ.процессов. Мат-кое направление зародилось в Англии.Представители(У.Петти,В.Госсета,Р.Фишер) этого напр.ставили задачей выявить закономерности взаимосвязей эк-ких явлений.Русские статистики:Ломоносов,Семёнов…. Ст-ка – это самостоятельная общ-ная наука,к-ая колич-ную сторону массовых обществ. явлений неразрывно связ. с их качеств.стороной в конкр. условиях места и времени. Осн.черты ст-ки: - изучает явления общ-ой жизни и имеющ.общ.значимость,но эти явления м. хар-ть и измерять кол-ными показателями,к-ые на опр. ступени м. переходить в новое качество. - ст-ка даёт хар-ку массовых явлений.Это даёт возможность освободиться от влияния случ.причин. Ст-ку интересуют варьирующие признаки:пол, возраст,образование,з/плата,стипендия.
Общая теория ст-ки разрабатывает общие принципы и методы,ст-кие исследования и явления. Экономич. ст-ки разраб-ют и анализир. Показатели сост.эк-ки,размещения производительных сил.Наличие матер,фин,трудресурсов и их исп-ния.Отрасли эк.ст-ки: -ст-ка на п/п, -с/х, -труда, -транспорта. Соц.ст-ка формирует сист.показателей,хар-щих соц. положение населения: народонаселение, здравоохранение, науку, политику и тд. Общая теор.ст-ки формирует необх. профессион. знаний у эк-тов, менеджеров, руквод. п/п.
МЕТОД СТАТИСТИКИ Научным методом ст-ки явл.метод диалектического материализма, т.е. общ-ные явления изменяются и развиваются,но т.к. ст-ка явл. наукой,то она дополняет этот метод своими приёмами. Метод ст-ки –это совокупность общих приёмов и принципов,исп-мых ст-кой д/изучения общественных явлений. Общие методы: -сравнение -анализ и синтез -индукция и дедукция -закон тождества -з-он исключённого 3-го -з-он достаточного основания(мысли необх подтвердить практикой) -и тд. Приёмы ст-ки: - метод массовых наблюдений, т.е. д/обобщения нужна совокупность фактов - метод группировок-это расчленение разнородных явлений на однородные,а затем их хар-ка. - метод обобщающих показателей даёт сводную хар-ку сов-сти фактов - и все темы общей ст-ки Широко исп. в ст-ке и спец раздел мат-ки- мат.ст-ка.
ЕДИНАЯ СИСТЕМА УЧЁТА И СТАТИСТИКИ РБ - оперативный учёт-это регистрация отдельных фактов в момент их свершения и близких к нему (явка студентов,выпуск продукции).Ведётся в натуральном выражении,необх. д/операт. руководства. - бух.учёт- учёт движения матер. и дел. ресурсов п/п и необх д/выявления рез-тов их деятельности. - межотраслевые и нар.хоз.связи выявляются только ст-кой. - статистич.учёт- межсторон.учёт явлений в масштабе п/п, отраслей. Д/этого он исп.данные операт. и бух. учёта.Они взаимосвязаны и едины.
ФУНКЦИИ И ЗАДАЧИ СТАТИСТИКИ. 1-ой осн.ф-цией ст-ки явл. познавательная, т.е.ст-ка устанавливает закономерности общего развития,начиная с бригад и участков и заканчивая всем народным хоз-вом в целом.Этими данными пользуются и др.науки(экономика, организация и др.) Управленческая ф-ция. На основе анализа работы за прошедший период принимаются новые планы,организуются и контр-ся их выполнение. Т.обр.,ст-ка выступает необх. эл-том гос.управления. Стимулируящая ф-ция. Планируемые орг-цией показатели д.учитывать потребности нар.хоз-ва и нацеливать их работу на конечный рез-тат. В принципе ст-ки показатели м.оказывать полож. или отриц.влияние на общественное время. Ф-ции и задачи ст-ки взаимосвязаны. Нельзя успешно управлять процессами общ. жизни без осущ.позноват.ф-ции.С др.стороны опыт упр-ния исп. д/новых обобщений в том числе оценки кач-ва показателей,т.е. на сколько они прогрессивны.
ОРГАНИЗАЦИЯ СТАТИСТИКИ В РБ Гос.ст-ка явл. составной частью информационной сист. РБ,к-ая призвана обеспечить гос.органы, СМИ, научно-исслед. орг-ции,общ-ные объединения и население статистической инф-цией. Осн.задачи гос.ст-ки: 1.сбор, обработка, обобщение и анализ инфы о процессах,происходящих в эк-кой и соц-ой жизни РБ. 2.обобщение и прогнозирование развития нар.хоз-ва. 3.повышение кач-ва инфы. 4.повышение оперативности инфы на ЭВМ. 5.формирование бухгалтерских ст-ких показателей в соот. С требованиями межд.бух.учёта и сист.нац.счетов наиб. полно отвеч.требованиям рын. эк-ки. Органом гос.ст-ки явл. Министерство ст-ки и анализа. Структура:упр.ст-ки г.Минска,имеются областные, районные и городские.В Министерстве имеются упр-ния ст-ки:промышленности,с/х, соц.ст-ки, матер-ых ресурсов, планво-фин; отделы:населения, торговли, кап. стр-ва, транспорта и др. В составе областных имеются упр-ния:соц.ст-ки, транспорта и услуг, торговли и финансов, промышленности, АПР,с/х, труда и з/пл. В составе Минского гор.упр-ния имеются отделы:промышл. и охр.окр.среды,труда и зарплаты,матер.ресурсов,транспорта,бюджетов,финансов и торговли. Сист.гос.ст-ки основана на терр. произв. принципе,т.е.1)п/п по терр-ии отчитываются перед органами ст-ки. 2)централизация всей учётной ст-кой работы в органах гос.ст-ки 3)механизация и автоматизация всех работ на базе применения ЭВМ. Сущ-ет и ведомственная ст-ка,к-ая ведётся в министерствах ведомствах орг. И п/п.Ведомст.ст-ка вып-ет работы,связанные с получением, обработкой и анализом инфы,необх. д/оперативного руководства.Д/этого имеются ячейки, секторы, отделы и упр-ния. Переход к рын.эк-ке, широкое межд.сотрудничество и полная самостоятельность и ответст. п/п за рез-ты работы треб.глуб.анализа эк-ких явлений и процессов на п/п всех форм собственности. В связи с этим,значение органов ведом.ст-ки возрастает.
СТАТИСТИЧЕСКОЕ НАБЛЮДЕНИЕ С развитием рын.отнош. роль информ.базы возрасла, возникла потребность в изучении влияющ.факторов. Важным ресурсом в управлении стала информация. База инф-ции формируется в рез-те наблюдения. Статист.наблюдение - планомер.науч.организованный сбор данных по явлениях и процессах общ.жизни.Наблюдение нач-ся с получ-я инфы,к-ая разнообразна по содержанию и способам получения(перепись населения,отчётность п/п).При наблюдении регист-ся признаки всех единиц совокупности. В рез-те получаем анкеты,записи регистраторов.Материал систематизируется в процессе обработки и исп. д/анализа и выводов,поэтому он д.б. качественным,т.е. отраж.реальн. жизнь. Наблюдение д.б массовым,иметь программу и план, способы, средства и сроки учёта фактов, контроль получ.данных. Процесс наблюдения сост. из составления плана наблюдения,его подготовки(печатание бланков,инструкций),пр-во наблюдения и контроль данных. Кроме того,сост-ся прог-ма обработки, а также фин.часть. ПРОГРАММНО-МЕТОДОЛОГИЧЕСКИЕ ВОПРОСЫ НАБЛЮДЕНИЯ. Программа - осн.вопрос наблюдения. Она опр-ся её задачами(изучение произв-сти труда) Программа - перечень вопросов или признаков, на к-ые д.б. получены ответы по един.наблюдения. Задачи наблюдения опр.цель, а цель опр-ет объект наблюд. Прога наблюд. включ. наиб. важные признаки явлений.В ней не д.б. лишних вопросов, а только те, на к-ые м. получить достоверные ответы и они не должны вызывать подозрений у опрашиваемых лиц. Вопрос д.б. чётким,иметь подсказки и без альтернатив.вопр. Объект наблюдения –совокупность явлений и процессов, к-ые подлежат исп-нию. Объект набл. – статист.совокупность, сост-ая из отдел единиц. Единица наблюдения – эл-т совокупности,по к-му собираются данные(Отдельный чел при переписи населения,а семья при изучении бюджетов).Ед.набл. зависит от задач исследования. Стат.формуляр –бланк с вопр. и свободным местом для ответа(карточные и списочные).Карточные предназнач. д/регистр-ии сведений по 1-ой единице.Списочные –д/регистр. сведений по 2 и более единицам. Инструкция –пояснение к заполнению бланка-формуляра.Она опр-ет цели и задачи набл.,объект и единицу,порядок оформления документации, срок отправки, а самое гл. разъясняет вопросы формуляра.
ОРГАНИЗАЦИЯ НАБЛЮДЕНИЯ. При орг-ции наблюдения необх. решить след. вопросы: 1) об органах наблюд. (Это органы гос.ст-ки,их представители или ведомств.органы) 2) срок или время проведения набл. (отчётность.перепись). Срок набл. д.б. кратким и max приближённым к критич. моменту, иначе сведения устареют. 3) место набл. Вопрос важен д/явлений, перемещающихся в пространстве(люди, станки, самолёт). Перепись м.происходить по месту постоян. проживания, при изуч. обеспеченности жильём или врем.прожив. 4) Способы регистрации: -непосред.набл; -докум.сп-об; -опрос людей; -исп-ие АБД;
СТАТИСТИЧЕСКАЯ СВОДКА. В рез-те набл., мы получаем данные по каждой единице, но правильно собранные данные не гарантируют правильных выводов. Д/их получения факты надо обобщить: для этого надо провести сводку первичных материалов. Т.обр., сводка явл. 2-ой ступенью исследования. Статист. сводка -э научная обработка первич. материалов набл. д/хар-ки сов-сти обобщ. показателями. Сводка обобщает материал, переходит от единичных фактов к общим закономерностям. Д\этого исп-ся группировки. Хотя сводка и явл. второй ступенью исследования, но уже в процессе набл. м. обнаружиться хар-ные изменения в распределении единиц, что даёт возможность потом сгруппировать материал. Сводка сост. по ранее разработанной программе, к-ая опр-ся её задачами. В плане сводки предусматривается очерёдность обработки мат-ла, кто проводит, сроки, … Сост. эл-ты сводки: 1)программа, определяющая применяемые группировки и систему хар-ную сов-сть показателей; 2)подсчёт групповых и общих итогов; 3)оформление в виде таблиц. В процессе сводки проверяют полноту охвата единиц и кол-во полученной инфы.
МНОГОМЕРНАЯ ГРУППИРОВКА Т.к. нельзя брать много признаков(более 3х признаков и 4х интервалов), то для решения задач многомерной груп-ки применяется один из методов стат-кой теории распознавания образцов – кластерный анализ. Реализация этого метода связана с исп-ем ЭВМ. Напр., имеем совок-сть стр-ных орг-ций, хар-щихся объёмом СМР, числом рабочих, произв. труда, наличием стр. машин и механизмов. Группировка орг-ций производится одновременно по всему набору признаков. Этот набор обр-ет «признаковое пространство», где каждому признаку придаётся смысл координаты. Если в наборе n признаков, то каждый объект рассм-ся как точка в n мерном пространстве. Задача многомерной группировки сводится к выделению сгущений точек в этом пространстве. Мерой близости между критериями м. служить различ. критерии(евклидово пространство). Xki – значение k-го признака в i-том объекте Xkj - значение k-го признака в j-том объекте Чем меньше это расстояние, тем больше близость. ВТОРИЧНАЯ ГРУППИРОВКА Вторичная группировка выступает особым видом. Вторичная гр-ка – образование новых групп на основе ранее проведенной гр-ки. Необходимость в ней выступает в 2х случаях: 1)когда нужно ранее выполненные группы укрепить, т.е. сделать их более типичными(месячные уровни объединить в квартальные) 2)если материалы собраны разными людьми и с разным интервалом образованы группы. Перегр-ка производится путём дробления групп по принципы пропорциональности. ОРГАНИЗАЦИЯ СВОДКИ Орг-ция сводки м. идти ч/з гос-ную или ведомственную ст-ку.Теперь преобладает гос.ст-ка. Это обеспечивает гос. интересы, сокращает объёмы работ, даёт возможность применять ЭВМ. При децентрализованной сводке первичные матер-лы сводятся в пределах вышестоящих орг-ций, к-ые передаются вышест-му звену. По сп-бу вып-ния сводка м.б. ручной и автоматизированной. В связи с появлением ПК, созданием автоматизир. раб. мест, разраб-ие пакетов прикладных прог,ручная сводка не применяется. Автоматизир. сводка вып-ся на ЭВМ и складывается из ряда операций: 1)перенос данных из первичных док-тов на носители инфы; 2)контроль качества переноса; 3)сортировка данных по группам; 4)табулирование, т.е. вып-ние выч. операций по отдельным показателям, группам и по всему массиву данных.
СТАТИЧСТИЧЕСКИЕ ТАБЛИЦЫ Рез-ты сводки даются в виде стат. таблиц. Это позволяет итоговые данные наблюдения легко читать, сравнивать и анализировать. Стат. таблица –это рациональная форма изложения и обобщения данных об общественных явлениях. Таблицы позволяют сжато и компактно изложить рез-ты сводной обработки данных наблюдения. Достигается это тем, что объекты и хар-щие их показатели располагаются в опр. системе, позволяющей внести их наименоания в виде общих д/них заголовков. Составными частями и эл-тами табл. явл.:
Каждая табл. имеет общ. заглавие. Название д.б. точным и ясным, выражать смысл цифр, указ. террит. или период времени к кот. они относятся и ед.измерения. Каждая табл. имеет подлежащее и сказуемое. Подлежащее –объект изучения (рабочие,бригады) Сказуемое –показатели, хар-щие объект(производитнльность, объёмы СМР). По характеру подлежащего табл. делятся на простые, групповые, комбинационные. Простые –табл., в подлежащем кот. нет группировок. Они б. перечневыми, террит. И хронологическими. Приводится перечень ед-ц, сост. объект изуч. В терр. Табл. приводится перечень терр.(стран,обл….). В хронолог. табл. приводятся периоды времени, даты о сказуемом показателей(СМР за к.-то годы) Групповой наз табл., в подлежащем кот. выделены группы, обр. по 1-му признаку, зависимость часовой з/пл от стажа работы. Комбинац. наз. табл., в подлежащем к-ой выделены группы по 2-ум и более признакам (зависисимость часовой з/пл от стажа раб. и прохождения обучения). Простые табл. дают инфу д/осущ. контролир. ф-ции, а групповые и комбинационные д/научно-познават. целей. Нуна уметь читать и анализировать табл. Сначала знакомятся с названием табл., заголовками подлеж. и сказуемых, опр-ют хар-щую табл., устанавливают ед.измерения, время, а потом приступают к анализу. Правила построения табл.: 1. небольшие по размеру 2. название табл., строки подлеж. и сказуемого д.б. точными, краткими и ясными. 3. д.б.итоги и ед.измерения, сноски.. 4. нулевые значения признака обозн. «―», если нет сведений, то …; 5. д.соблюдаться принятая точность величин; 6. в больших табл. после каждых 5 строк нуна ставить двойной промежуток 7. графы и строки номеровать 8. взаимосвяз. и зависимые данные целесообразно располагать рядом. 9. числа ед. под единицами, десятки под десятками, запятая под запятой. АБСОЛЮТНЫЕ ВЕЛИЧИНЫ.
ВИДЫ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН. В практике статистики применяются различные виды относительных величин. Отн.вел-на планового задания -отношение планового задания к фактическому достигнутому уровню. Измеряется в %. Отн. вел-на динамики -характеризует изменение одноимённых показателей во времени и получается путём сопоставления показателя каждого периода к прешествующему или к первоначальному.Поэтому они наз-ся цепными или базисными. Измеряется в %, коэф-ах. Отн. вел. вып-ия плана -отношение факта к плановым заданиям. Если У0-базис. период,Упл-планов.задание,Уф- фактич.достигнутый уровень, то Относ.вел. Упл Отн.вел. Уф Отн.вел. Уф план.задания= У0 ; вып.плана= Упл ; динамики= У0 ; Отн.вел. структуры характеризует удел. вес части в общем итоге. Измеряется в коэф-ах или %. Напр., в группе 30 чел. Из них 22 девушки, 8 парней. Удел.вес девушек-73,3%, парней-26,7%. Отн.вел.координации хар-ют соотношение отдел. частей целого, одна из которых принята за базу сравнения. Напр.,22:8=2,75 девушки приходится на 1 мальчика. Отн.величина является дополнением к характеристике структуры. Отн.вел. сравнения или наглядности характеризует соотношение одноимённых показателей, относится к различ.объектам иои территориям, но за один и тот же период или момент времени. Напр.,соотнош-е объёмов СМР (2 общестр. СУ) близких по своим возможностям. Отн.вел. интенсивности харак-ет степень распространённости данного явленя в опред. среде. Многообразие изучаемых величин общест.явлений требует дифир-го использования абс. и отн. величин. Отн. величины не следукт отрывать от базы. Напр., в 2 близких по своим возможностям СУ объём СМР возрос в 1-м на 15%, во 2-м на 7%. Но объём СМР в 1м СУ-100млн., во 2м-300млн. ∆СМР=150 млн.руб; ∆СМР=25 млн.руб. Только комплекс применения абс. и отн. величин даёт всестороннюю характеристику изучаемого явления. СРАВНИТЕЛЬНЫЕ ДИАГРАММЫ. 1.Столбиковые: Объём СМР СУ за 2004-2006 гг.
2.Столбиковые, скомбинированные группировкой показателей по 2-м признакам: Динамика численности рабочих СУ по полу за 2004-2005 гг.
3.Полосовые (столбчатые, развёрнутые на 900): Динамика объёмов СМР
4.Ступенчато-столбчатые и ступенчато-полосовые:
5.Для квадратных и круговых (из сравниваемых величин извлекаем кв.корень и в принятом масштабе берём сторону квадрата или rкруга).
Замечание: площади сравнивать труднее, чем высоты! СТРУКТУРНЫЕ ДИАГРАММЫ. Структ. диаграммы бывают: Столбиковые: Динамика численности СУ-1 за 2004-2006гг. по полу:
Полосовые -наиболее частого использования. Структура себестоимости СМР (в %)-прямых затрат: Материалы и конструкции -60 1% - 3,60; Зарплата-25 60*3,6=2160; Стоим-ть экспл-ци-15 25*3,6=900; 15*3,6=540 Замечание: При мален. отличии в размерах составляющих она получается плохо! Секторные с долевой группировкой:
Стоклеточная или шахматная:
1 кл=1%; структура:30;45;25. Балансовые:
Знаки Визара: 1) простой знак Визара обозначает объём явлений, являющихся результатом перемножения 2-х др. признаков: V СМР = С*Производительность труда
2) сложный промышленный знак Визара:
ДИНАМИЧЕСКИЕ ДИАГРАММЫ Для изображения динамики м. применятся столбиковые, квадратные, секторные и круговые диаграммы. Но чаще применяются линейные диагр.
Строятся в системе координат прямоугольной, на одном графике м. построить несколько диаграмм. Иногда строят радианные диаграммы: берут данные не менее чем за 3 одноимённых периода и строят по средним: ИЗОБРАЗИТЕЛЬНЫЕ ДИАГРАММЫ При построении изобразительных диаграмм геометр. фигуры заменяют символами, связанными с изобразительными явлениями.Напр., снопы, цистерны нефти, рулоны бумаги, телевизоры.
Диаграммы отличаются друг от друга размером или объёмом явлений, изображаемых набором фигур одинаковых размеров. ТЕМА 5. СРЕДНИЕ ВЕЛИЧИНЫ ВИДЫ СРЕДНИХ. 2 категории средних величин: степенные и структурные (описательные). Степенные ве-ны: среднеарифметические, среднеквадратические, средне- геометрические. Расчёт этих ве-н выражается математически. Общая формула степенных средних ве-н: Среднее арифметическое, гармоническое, квадратичное могут быть простыми (если каждое отдельно значение признака встречается 1 раз) и взвешенными (если встречается несколько раз).
Эти степенные средние ве-ны, исчисленные д/одной и той же совокупности единиц имеют различные количественные значения и чем больше показатель степени (m), тем больше ве-на средней. Х 0геом< Х -1гарм< Х 1арифм < Х 2квадр. Это сво-во средних называется мажорантностью. Применение вида средних определяется материальным содержанием изучаемых явлений; наиболее часто применяются средние арифметическое и гармоническое. ДРУГИЕ ВИДЫ СРЕДНИХ. Среднее гармоническое применяется, когда известны индивидуальные значения какого-либо признака и общий итог совокупности, но неизвестны частоты f. (Х = ∑x*f/∑f, где x*f = Ф; если f неизвестно, тогда: Х = ∑Ф/∑f = ∑Ф/∑x-1*Ф) Среднее геометрическое применяется при вычислении средних темпов динамики. Среднее квадратичное применяется д/ характеристики вариации признака.
РЯДЫ РАСПРЕДЕЛЕНИЯ. В процессе группировки производится распределение единиц совокупности по значениям группировочного признака. В результате получается 2 колонки: одна содержит перечень значений признака, другая – данные о численности единиц. Такое распределение единиц совокупности по значению группировочного признака назыв. рядом распределения (РР). РР могут быть образованы по качественным атрибутивным (атрибутивные) и количественным (вариационные) признакам. Различают: дискретные вариационные ряды, интервальные вариационные ряды. Чаще применяются интервальные вар.ряды. При их построении следует соблюдать ряд условий: группы и подгруппы должны существенно отличаться друг от друга; лучше применять неравные интервалы, а применение равных интервалов даёт возможность исп-ть математические приёмы анализа явлений; чем больше колебание признака, тем больше должно быть групп; не должно быть единичных и нулевых групп. Частоты – абсолютные численности интервалов ряда. Частоты, выраженные в долях или %тах ряда – частности. В интервальных рядах с неравными интервалами непосредственное сравнение численности затруднено, т.к. меняются и интервалы и их численности. В этом случае определяют плотность распределения (отношение частот или частности к ве-не интервала). Плотность может быть: абсолютной (рассчитана на основе частот), относительной (рассчитана по частностям). Частоты в вариационных рядах с равными интервалами и плотностью распределения в рядах с неравными интервалами выр-ют определённую закономерность распределения. Д/ха-ки РР могут исп-ся и накопленные частоты; они д/каждого интервально ряда рассчитываются путём последующего суммирования частот всех интервалов (рассчит-ся в восходящем и нисходящем порядках). ПОКАЗАТЕЛИ ВАРИАЦИИ. Размах вариации: Хmax – Xmin; зависит только от крайних значений, поэтому применим только д/достаточно однородной совокупности; нужны показатели, учитывающие колеблемость всех значений признака. Среднее линейное отклонение – среднее арифметическое из абсолютных значений отклонений всех значений признака от средней (d): d = ∑|x- x| /n; d = ∑|x- x| f /∑f Дисперсия (σ2): σ2= ∑(x- x) 2/n; σ2= ∑(x- x)2f/∑f; д/альтернативного ряда: σ2= р(1-р)=р*q, где р – доля единиц, обладающих определённым признаком, q - доля единиц, не обладающих определённым признаком. Среднее квадратичное (= стандартное отклонение) (σ): σ = корень из ∑(x-x)2/n; σ =корень из ∑(x- x)2f/∑f; д/умеренно ассиметричного распределения: σ=1,25d, d=0,8σ Среднее линейное и квадратичное отклонения – ве-ны именованные, но даже если они равны между собой, а средние арифм-ие различны, то д/каждой совокупности они имеют различное значение. Поэтому отдельно рассчитывается коэффициент вариации: 1) коэффициент осцилляции: V=(R/ x)*100%; коэффициент линейного отклонения: V=(d/ x)*100%; коэффициент вариации: V=(σ/ x)*100%. Коэффициент вариации исп-ся не только д/сравнительной оценки вариации, но и д/ха-ки однородности совокупности. Если он меньше 33%, то совокупность однородна и её можно ха-ть средней ве-ной. Если совокупность неоднородна, но нужно рассчитывать показатель вариации. Показатель вариации является мерой надёжности средней. Чем меньше d, σ2, V тем однороднее изучаемая совокупность и надёжнее полученное среднее. Согласно правилу 3ёх σ (сигм), в нормально распределённых или близких к ним рядах распределения отклонение не превосходит 3 σ встреч в 997 случаях из 1000, не > 2 σ в 954 случаях из 1000, не > 1 σ 683 из 1000. ДИСПЕРСИЯ И ЕЁ СВО-ВА. Сво-ва дисперсии: · Дисперсия постоянного числа равна 0 · Если все значения признака уменьшить или увеличить на какое-либо число А, то дисперсия от этого не изменится, т.е. дисперсию можно вычислить по отклонениям от какого-либо постоянного числа А · Если все значения признака уменьш/увел-ть в К-раз, то дисперсия от этого изменится в К2-раз, т.е. можно все значения признака уменьшить в К-раз, вычислить дисперсию, а затем умножить её на это постоянное число в квадрате. · Дисперсия признака равна разности среднего квадрата значений признака и квадратом их средней: σ2= х2 – х 2; x2 =∑x2f/∑f · Расчёт дисперсии (способ моментов или от условного нуля): σ2=∑(x-a)2*f/∑f -(x -a)2 ПРАВИЛО СЛОЖЕНИЯ ДИСПЕРСИЙ. Общая вариация в совокупности является результатом действия всех причин и измеряется общей дисперсией: σ2= ∑(x- x)2f/∑f. Вариации групповых средних измеряются отклонением групповых средних от общей средней, и отражает влияние фактора, по которому произведена группировка: σ2= ∑(xi - x)/n = ∑(xi - x)2*f/∑f, где xi – групповые средние. Остаточная или внутригрупповая вариация выражает отклонение отдельных значений признаков в каждой группе от их групповых средних, и отражает влияние всех прочих факторов, кроме положенного в основу группировки. Остаточная вариация будет отражать среднее из групповых дисперсий: δi2= ∑(xi- xi)2/ni; σi2 = ∑ σi2fi/∑ fi Общая вариация признаков совокупности определяется как сумма вариаций группировочных средних и остаточные вариации: σ2= δ2+ σi2. Суть равенства: общая дисперсия, возникающая под воздействием всех факторов должна быть равна сумме всех дисперсий, возникающих за счёт факторов группировки и под влиянием прочих факторов; это равенство известно как правило сложения дисперсий; оно позволяет находить общую дисперсию по групп-ым показателям. Коэффициент детерминации (отношение межгрупповой дисперсии к общей) = δ2/ σ2; его значение максимально и равно 1 если δ2=σ2; его значение минимально и равно 0, если δ2=0 ТРЕБОВАНИЯ К ОЦЕНКАМ. Д/оценки параметра могут исп-ся любые оценки. Д/того, чтобы выбрать лучшую из них, нужно иметь критерий сравнения оценок (они также могут быть разными в зависимости от цели д/которой строится оценка).Любой критерий определяется выбором меры близости оценки к истинному значению оцениваемого параметра, т.е. рассеивание случайной ве-ны х около х должно быть наименьшим. Оценки бывают:1) несмещённые: математическое ожидание параметра равно оцениваемому параметру, т.е. параметр распределения выборки и ГС совпадают; в противном случае имеем смещённую завышенную/заниженную оценку; предпочтение отдаётся той, которая имеет наименьшее рассеивание около оцениваемого параметра; 2) эффективная: это несмещённая оценка, имеющая наименьшую дисперсию среди всех возможных оценок; 3) состоятельная: оценка, которая подчиняется закону больших чисел, т.е. при достаточно большом числе наблюдений с вероятностью близкой к 1 можно утверждать, что разность между параметром распределения выборки и ГС небольшая. (т.е. при ↑ числа единиц выборки становится менее вероятной возможность значительной ошибки в оценке неизвестного параметра); 4) достаточная: оценка, исп-щая всю инфо относительно оцениваемого параметра, содержащуюся в выборке. ОШИБКИ СЛУЧАЙНОЙ ВЫБОРКИ. При случайном отборе каждая единица имеет равную возможность попасть в выборку. В случайной выборке ошибка, которая имеет ту же вероятность, что и выборочное среднее → нужна оценка выборочных данных. Ошибки выборки: средняя, предельная. Дисперсия выборочной средней в n раз меньше дисперсии ГС: ПОНЯТИЕ И ЗАДАЧИ КОРРЕЛЯЦИИ Различают связи: 1) функциональная; связь, при которой каждому значению факторного признака соответствует 1 или несколько строго определённых значений результативного признака (напр, Sкруга=ПR2); такие связи характерны д/естественных наук, они являются точными и полными, обнаруживаются на небольшом числе единиц; 2) корреляционная связь; связь, при которой каждому значению факторного признака соответствует среднее значение результативного признака при большом числе наблюдений; эти связи могут быть приближённые, неполные. Корреляция – соотношение, соответствие; отношение связи между переменными ве-нами. Выделяют корреляции: 1) парная: y=f (a), y=f(b) (влияние отдельных факторов на изучаемый); 2) множественная: y = f (a,b,c) (влияние нескольких факторов на изучаемый). В зависимости от направления действия связи быва
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 301; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.151.198 (0.014 с.) |


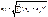
 Обобщающие показатели бывают экстенсивные (объёмные) и интенсивные (качественные). Объёмные показатели -это обычные абсолютные величины. Интенсивные показатели -подразделяются на относительные и средние. Абсолютными величинами наз.показатели, выражающие размеры, объёмы и уровни общест. явлений и процессов. Они широко исп-ся в планировании, в учёте и при эк. анализе.По способу выражения абс. вел-ны бывают: индивидуальные,гпупповые, общие. Индивидуальные выражают размеры количественных признаков у отдельных единиц. А групповые и общие – у отдельных групп или у всех единиц изучаемой совокупности, т.е. они получаются путём суммирования индивидуальных. Абсол. величины всегда числа именованные, т.е имеют ед-цы измер-я:натуральную (тонн,м2,штук) и условно-натуральную (кирпич, лист шифера, тонна цемента). Для обобщения данных используются стоимостные или денежные единицы измерения. Абсолютные показатели м.б измерены с различной степенью точности.
Обобщающие показатели бывают экстенсивные (объёмные) и интенсивные (качественные). Объёмные показатели -это обычные абсолютные величины. Интенсивные показатели -подразделяются на относительные и средние. Абсолютными величинами наз.показатели, выражающие размеры, объёмы и уровни общест. явлений и процессов. Они широко исп-ся в планировании, в учёте и при эк. анализе.По способу выражения абс. вел-ны бывают: индивидуальные,гпупповые, общие. Индивидуальные выражают размеры количественных признаков у отдельных единиц. А групповые и общие – у отдельных групп или у всех единиц изучаемой совокупности, т.е. они получаются путём суммирования индивидуальных. Абсол. величины всегда числа именованные, т.е имеют ед-цы измер-я:натуральную (тонн,м2,штук) и условно-натуральную (кирпич, лист шифера, тонна цемента). Для обобщения данных используются стоимостные или денежные единицы измерения. Абсолютные показатели м.б измерены с различной степенью точности.






 М.б. на полукругах:
М.б. на полукругах: 



 -уголь;
-уголь;  -нефть
-нефть , где m – показатель степени средней, n – число единиц, х – отдельное значение признака, х – степенные средние
, где m – показатель степени средней, n – число единиц, х – отдельное значение признака, х – степенные средние


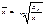



 П - произведение
х-темпы роста
П - произведение
х-темпы роста
 , если дисперсия ГС известна, можно применить формулу д/выборочной дисперсии:
, если дисперсия ГС известна, можно применить формулу д/выборочной дисперсии:  ; однако:
; однако:  . Соотношение между
. Соотношение между  и
и  :
:  , но при большом n
, но при большом n  → 1, следовательно, ошибка выборки приближённая. Предельная ошибка выборки:
→ 1, следовательно, ошибка выборки приближённая. Предельная ошибка выборки:  , µ - средняя ошибка выборки, Т – коэффициент доверения (зависит от вероятности определения ошибки, теории выбранного метода и др.). Теория Чебышева: при большом числе наблюдений ошибка будет незначительной. Теорема Бернулли: при достаточно большом объёме выборки вероятность расхождения между ω (доля признака выборочной совокупности) и р (доля признака в ГС) → 1:
, µ - средняя ошибка выборки, Т – коэффициент доверения (зависит от вероятности определения ошибки, теории выбранного метода и др.). Теория Чебышева: при большом числе наблюдений ошибка будет незначительной. Теорема Бернулли: при достаточно большом объёме выборки вероятность расхождения между ω (доля признака выборочной совокупности) и р (доля признака в ГС) → 1:  ; средняя ошибка д/альтернативного признака:
; средняя ошибка д/альтернативного признака:  ; средняя ошибка доли признака:
; средняя ошибка доли признака:  . Все приведенные формулы применяют к повторному, а чаще бесповторному отбору:
. Все приведенные формулы применяют к повторному, а чаще бесповторному отбору:  , если пренебречь единицей при больших N/ этот множитель всегда меньше 1, но предельная ошибка выборки бесповторного отбора всегда меньше, чем при повторном отборе.
, если пренебречь единицей при больших N/ этот множитель всегда меньше 1, но предельная ошибка выборки бесповторного отбора всегда меньше, чем при повторном отборе.


