
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выявление влияния отдельных факторов на изучаемый.Содержание книги
Поиск на нашем сайте
Применение методов корреляционного анализа даёт возможность выражать связь между признаками аналитически и придавать количественное значение. К примеру, связь между признаками может быть выражена уравнением прямой: 2) Параметры Связь между признаками прямая, поэтому нужно разработать мероприятие по усилению влияния фактора. Может быть криволинейная зависимость между признаками: парабола, гипербола. Способ решения будет аналогичен. Кроме парной корреляции можно вычислить зависимость одно признака от нескольких, т.е. мы будем иметь уравнение множественной регрессии. МНОЖЕСТВЕННАЯ КОРРЕЛЯЦИЯ. Методология решения задач множественной корреляции: установление наличия связи, установление тесноты связи, формы связи, влияние отдельных факторов на общий результат. Отличительные особенности этой методологии: иногда приходится укрупнять единицы наблюдения (брать не рабочих, а бригады; не строительные управления, а тресты); численность исследуемой совокупности должна превосходить число факторов в 6-7 раз; должен быть тщательный отбор факторов и их содержательный анализ д/выбора уравнения связи. Д/этого вычисляют х, σ,σ 2, v и коэфф-т тесноты связи. Существенным в составлении уравнения регрессии является выбор типа функции. Модель должна иметь математическое решение → её нужно выразить в форме одной из известных функций. Как и при парной корреляции, указание на функций можно получить из логического анализа предыдущего опыта, экспертных оценок, изучение исходных эмпирических данных. Чаще всего д/определения вида уравнения связи исп-ся способ перебора различных уравнений: большое число уравнений связи реализуется на ЭВМ с помощью специально разработанного алгоритма перебора с последующей проверкой, главным образом на основе критерия Стьюдента (очень трудоёмко). Д/определения тесноты связи при множественной корреляции пользуются коэффициентом множественной корреляции предварительно вычислив парной корреляции. Если х зависит от у и z, то парные коэфф-ты вычисляют по формулам: На их основе вычисляют коэфф-т множественной корреляции: ПРИМЕНЕНИЕ КОРРЕЛЯЦИОННОГО МЕТОДА АНАЛИЗА СВЯЗЕЙ. Возможность широкого применения метода корреляционного анализа ещё в недалёком прошлом сдерживалось большим объёмом расчётов. Сегодня широкое применение получили пакеты прикладных программ по статистике, ликвидировавшие эти ограничения: Excel, Supercalc, Stafgraf и др. В настоящее время корреляционный анализ широко применяется в экономических целях: при анализе произв.-хозяйственной деятельности предприятия, использование основных фондов и др. ТЕМА 9.РЯДЫ ДИНАМИКИ. ПОНЯТИЕ О РЯДАХ ДИНАМИКИ (РД) И ИХ ВИДЫ. Обществ явл-я нах в постоянном развитии в пространстве и вр.Меняется их объем и структура.статист показатели, хар-щие изм-е явл-ий во времени- динамич или времен-е ряды. Показатели за кажд п-од,хар-ие изуч-й объект- ур-ни ряда. Различ интерв-е и моментные РД, интервальный ряд -хар-ет размеры явл-я за опред п-оды времени(объемы СМР,среднемес зпл) моментный ряд -хар-ет состояние явл-я на опред момент времени(число студентов к концу 1ого часа, к концу 2ого часа).Разница:в интерв ряду кажд ур-нь относится к определенному промежутку времени, а суммирование рядов дает некот итоги.В моментном ряду слагаемые повторяются в разл ур-нях ряда и суммировать ур-ни нельзя.они хар-ют изм-е явл-ий за какой-то п-од времени. Замечание:сопоставляемые данные динамич рядов д б однородны по эк содержанию.для этого д соблюд-ся ряд условий:д б обеспечена одинак полнота охвата разл частей явл-ия, одинаковость границ территории или стр-ра, д б равенство анализируемых п-дов.
ПОКАЗАТЕЛИ РЯДА ДИНАМИКИ (РД) РД м анализ-ть при пом ряда показ-лей,опред-их хар-р и интенсивность колич-ых изм-й явл-й т.к. сопоставление самих рядов имеет ограниченное применение.В рез-те сравнения ур-ней получ система абсолют и средних показателей РД. Абсолютные показатели РД: 1. абсолютный прирост-разность м/д данным ур-не и ур-нем,принятым за базу сравнения. (м б +/-) Бывает цепной и базисный. Δб=yi-y1, Δц=yi-yi-1 2. Темп роста-отношение данного ур-ня к ур-ню принятому за базу срав-я.(%). Коэф-т роста-в коэф-тах. Цепной и базисный. Трц=yi/yi-1*100%, Tpб=yi/y1*100% Произведение цепных темпов роста=базисному. 3. Темп прироста-отношение абсолютного прироста к базе (+/-). Изм-ся в % или коэф-ах. Тпр=Тр-100%; Тпр=Кр-1. Цепной и базисный. Тпрц=Δцi/yi-1 *100% Тпрб=Δбi/y1*100% 4. Абсолютн знач-е 1% прироста-отношение абсол прироста к темпу прироста(в %) или =1% базиса. ац=Δц/Тпрц*100%, аб=Δб/Тпрб *100% при сопоставлении динамики динамики развития 2х явл-й м исп коэф опережения(отношение темпов роста(прироста) за одинак отрезки времени). Коп=Тр1/Тр2, Коп=Тпр1/Тпр2.
|
||||
|
Последнее изменение этой страницы: 2016-06-29; просмотров: 228; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.120.103 (0.006 с.) |

 . В уравнении прямой х всегда известен, поэтому нужно найти
. В уравнении прямой х всегда известен, поэтому нужно найти  и
и  , представляющие собой среднее значение некоторых показателей, принимаемые в уравнении постоянными. Известно, что параметр ао является отрезком ординаты при х=0, а а1=tg угла наклона. Нахождение параметров производится по способу выравнивания наименьших квадратов. Линия связи должна обладать основными сво-вами ср.арифм: ∑d=0, ∑d2=min; если обозначить ординаты фактических точек поля корреляции через yi, а ординаты теоретических линий -
, представляющие собой среднее значение некоторых показателей, принимаемые в уравнении постоянными. Известно, что параметр ао является отрезком ординаты при х=0, а а1=tg угла наклона. Нахождение параметров производится по способу выравнивания наименьших квадратов. Линия связи должна обладать основными сво-вами ср.арифм: ∑d=0, ∑d2=min; если обозначить ординаты фактических точек поля корреляции через yi, а ординаты теоретических линий -  , то второе условие можно записать так:
, то второе условие можно записать так: 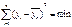 . Это условие и лежит в основе способа наименьших квадратов. Поскольку
. Это условие и лежит в основе способа наименьших квадратов. Поскольку  . Вычислив первые производные по
. Вычислив первые производные по  от этой ф-ии и приравняв каждую из производных к 0, мы сможем определить те значения
от этой ф-ии и приравняв каждую из производных к 0, мы сможем определить те значения  и
и  при которых
при которых 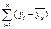 будет минимальной. После преобразований получим систему из 2ух уравнений: 1)
будет минимальной. После преобразований получим систему из 2ух уравнений: 1)  ,
, . Для нахождении
. Для нахождении  и
и  нужно найти ∑х, ∑у, ∑х2, ∑ху (данные берутся из представленной таблицы). Подставляя значения из предоставленной таблицы находим
нужно найти ∑х, ∑у, ∑х2, ∑ху (данные берутся из представленной таблицы). Подставляя значения из предоставленной таблицы находим  и
и  , затем эти значения подставляем в ур-ие
, затем эти значения подставляем в ур-ие  .
. и
и  ,
,  .
. ,
,  ,
, 




