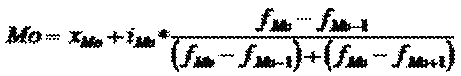Развитие явления во времени (динамику)

Статистика как наука

Статистика — это ряды цифр, которые характеризуют различные стороны жизни государства.

Статистика — это род практической деятельности людей цель которой сбор, обработка и анализ информации.

Статистика — это наука, разрабатывающая статистическую методологию т.е. набор приемов и способов сбора, обработки и анализа информации.

Таким образом, статистика — это общетеоретическая наука (комплекс научных дисциплин), которая изучает количественную сторону качественно определенных массовых социально-экономических явлений и процессов, иэ состав, распределение, размещение в пространстве, движение во времени выявляя действующие взаимозависимости и закономерности в конкретных условиях места и времени.

Объектом изучения статистики является общество, протекающие в нём процессы и закономерности развития.

Статистика как наука представляет собой целостную систему научных дисциплин:

Общая теория статистики — разрабатывает теорию статистического исследования, являющуюся методологической основой остальных отраслей статистики.

Социально-экономическая статистика (Макроэкономическая статистика). Использует методы общей теории статистики, изучает количественную сторону социально-экономических явлений и процессов на уровне национальной экономики.

Математическая статистика и теория вероятности. Изучает случайные величины, законы их распределени.

Международная статистика. Предетом международной статистики является количественная сторона явлений и процессов зарубежных стран и международных организаций.

Отраслевые статистики. Предетом изучения является количественная сторона деятельности различных отраслей экономики (Статистика промышленности, сельского хозяйства).

Общая теория статистики открывает курс изучения статистических дисциплин. Она является основополагающей дисциплиной для изучения отраслевых стастик, создаёт фундамент для усвоения и применения статистических методов анализа.

 

Предмет статистики — размеры и количественные соотношения качественно определенных социально-экономических явлений, закономерности их связи и развития в конкретных условиях места и времени.

Предмет статистики (статистика изучает):

Массовые общественные явления и их динамику при помощи статистических показателей. Требование массовости обусловлено действием закона больших чисел — при большом количестве наблюдений, действия случайных признаков взаимопогашаются. (численность населения, количество произведенной продукции)

Количественные и качественные явления (Цифровое освещение событий общества).

Количественную сторону общественных явлений в неразрывной связи с их качественным содержанием, наблюдает процесс перехода количественных изменений в качественные (закономерности).

Развитие явления во времени (динамику)

 

Абсолютные и относительные показатели вариации

Информация о средних уровнях исследуемых показателей обычно бывает недостаточной для глубокого анализа изучаемого процесса или явления. Необходимо учитывать и разброс или вариацию значений отдельных единиц, которая является важной характеристикой изучаемой совокупности. В наибольшей степени вариации подвержены курсы акций, объемы спроса и предложения, процентные ставки в разные периоды и в разных местах.

 

Основными показателями, характеризующими вариацию, являются размах, дисперсия, среднее квадратическое отклонение и коэффициент вариации.

 

Простейшим показателем является размах вариации. Он представляет собой разность максимального и минимального значений признака:

 

R=Xmax-Xmin.

 

Недостатком данного показателя является то, что он оценивает только границы варьирования признака и не отражает его колеблемость внутри этих границ. Этого недостатка лишена дисперсия, рассчитываемая как средний квадрат отклонений значений признака от их средней величины:

 

Q2 = ∑ (xi – x)2 / n - невзвешенная формула

 

Q2 = ∑ (xi – x)2 fi / ∑fi - взвешенная формула

 

коэффициент вариации измеряет колеблемость в относительном выражении, относительно среднего уровня.

 

Информативность показателей вариации повышается, если они рассчитываются для целей сравнительного анализа. При этом показатели, рассчитанные по одной совокупности, сопоставляются с показателями, рассчитанными по другой аналогичной совокупности или по той же самой, но относящейся к другому периоду времени. Например, исследуется динамика вариации курса доллара по недельным или месячным данным.

 

Показатели вариации могут быть использованы не только в анализе колеблемости или изменчивости изучаемого признака, но и для оценки степени воздействия одного признака на вариацию другого признака, т.е. в анализе взаимосвязей между показателями.

 

Для измерения вариации признака используют как абсолютные, так и относительные показатели.

 

К абсолютным показателям вариации относят: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, дисперсию.

 

К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение и др.

 

Статистическая методология

 

Основным условием правильного восприятия и практического использования статистической информации в рыночных отношениях является знание статистической методологии.

Статистическая методология – это система приемов, способов, методов, направленных на изучение количественных закономерностей, проявляющихся во взаимосвязи с социально-экономическими явлениями.

Статистическая методология включает три этапа исследования.

Первый этап: метод массовых наблюдений – это организованная регистрация собранных фактов о массовых социально-экономических, общественных явлениях и процессах.

Второй этап: сводка и группировка статистических данных – это систематизация первичных данных по признакам, объединяющим в качественно однородные группы.

Третий этап: анализ совокупных данных, полученных в результате сводки и группировки, при этом используются обобщенные показатели: абсолютных, относительных и средних величин, показатели вариации, ряды динамики, анализ взаимосвязей и индексы. На стадиях статистического исследования применяются специфические методы, которые и образуют статистическую методологию

 

Основные понятия и категории статистики

Теоретическую основу любой науки составляют понятия и категории к важнейшим из которых относятся стат. Совокупность, призн., вариация закономерность, стат. показателей. Стат. совокупность- множество соц. Эк. Объектов обледененных качественной основой, но отличающихся друг от друга отдельными признаками. Совокупности могут быть однородными и разнородными Совокупность называется разнородной если одни или несколько изуч. Сущ. Признаков её объектов явл. Общими для всех единиц, совокупность называется разнородной если в неё входят явления разного типа. Одна и та же совокупность единиц может быть однородна по одному признаку и неоднородна по другому. Единица статистической совокупности это каждый отдельно взятый (первичный элемент данного множества)Единица стат. совокупности характеризуется общими св-ми –признаками. Признак – это качественная особенность единицы совокупности. | По форме внешнего выражения признаки делятся на а) количественные – имеющие численное выражение, возраст, стаж работы и тд. Б)атрибутивные (качественные) признаки не имеющие непосредственного кол-ого выражения, в этом случайно отдельны еденицы совокупности различ. Своим содержанием. По характеру вариации признаки бывают: а) альтернативные которые могут принимать только два значения(пол человека) б)дискретные: количественные признаки которые могут принимать только отдельные значения без промежуточных значениях между ними. в) непрерывные – признаки способные принимать любые значения. Вариация – это различия в значениях того или иного признака у отдельных единиц совокупности. Закономерность- это форма проявл. Причинной связи выражающийся в последовательности регулярности событий с достаточно высокой степенью вероятности, если причины поражающие события не изменяются или измен. не значительно. При исследовании тенденций и закономерности развития общ. Явл статистика опирается на закон больших чисел, который говорит о том, что кол-ые закономерности массовых явлений отчетливо проявл. лишь в достаточно большом их числе. Стат показатель это полная оценка св.-в изм. Явления. Стат. показатели подразделяются на учетно-оценочные и аналитические показатели отражают объем или уровень изучаемого явл. Стат. показателшь имеет три обязательных атрибута: кол опр., места и времени

 

 

Сущность средней величины

 

Средняя величина - это обобщающая количественная характеристика совокупности однотипных явлений по одному варьирующему признаку. В экономической практике используется широкий круг показателей, вычисленных в виде средних величин.

 

Важнейшее свойство средней величины заключается в том, что она представляет значение определенного признака во всей совокупности одним числом, несмотря на количественные различия его у отдельных единиц совокупности, и выражает то общее, что присуще всем единицам изучаемой совокупности. Таким образом, через характеристику единицы совокупности она характеризует всю совокупность в целом.

 

Средние величины связаны с законом больших чисел. Суть этой связи заключается в том, что при осреднении случайные отклонения индивидуальных величин в силу действия закона больших чисел взаимопогашаются и в средней выявляется основная тенденция развития, необходимость, закономерность. Средние величины позволяют сравнивать показатели, относящиеся к совокупностям с различной численностью единиц.

 

 

7. Сущность, виды и формулы для вычисления средних показателей. Область их применения.

 

Средние показатели

Наиболее распространенной формой статистических показателей, используемых в социально-экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака статистической совокупности. Средние величины являются как бы «представителями» всего ряда наблюдений. Определить среднюю можно во многих случаях через исходное соотношение средней (ИСС) или ее логическую формулу:

.

Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:

Числитель исходного соотношения средней представляет собой ее определяющий показатель. Для средней заработной платы таким определяющим показателем является фонд заработной платы. Для каждого показателя, используемого в социально-экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней.

Следует еще добавить, что для того, чтобы более точно оценить стандартное отклонение для малых выборок (с числом элементов менее 30), в знаменателе выражения под корнем надо использовать не n, а n- 1.

 

 

 

Виды сводки

Различают простую и сложную сводку:

§ При простой сводке производится подсчет общих итогов по изучаемой совокупности.

§ При сложной сводке производится группировка единиц наблюдения, подсчет итогов по каждой группе и по всей совокупности, и представление результатов группировки в виде статистических таблиц.

Сводка называется децентрализованной если единое руководство работой осуществляется из центра, а непосредственная работа проводится на местах (обычно используется при обработке статистической отчетности).
Если же сбор и обработка данных проводится в одном месте, то сводка называется централизованной. Централизованная сводка обычно используется для обработки материалов единовременных статистических обследований.

Проведению статистической сводки и группировки предшествует разработка программы статистического наблюдения, состоящая из нескольких этапов: выбор группировочного признака, разработка системы статистических показателей.

Статистическая сводка должна проводиться по определенной программе и плану.

Сводка состоит из следующих этапов:

§ Выбор группировочного признака;

§ Определение порядка формирования групп;

§ Разработка системы статистических показателей для характеристики отдельных групп и совокупности в целом;

§ Разработка макетов статистических таблиц для представления результатов сводки.

 

Статистические таблицы

 

Статистическая таблица – это особый способ краткой и наглядной записи сведений об изучаемых общественных явлениях. Статистическая таблица позволяет охватить материалы статистической сводки в целом.

 

По внешнему виду статистическая таблица представляет собой ряд пересекающихся горизонтальных и вертикальных линий, образующих по горизонтали строки, а по вертикали – графы (столбцы, колонки), которые в совокупности составляют как бы скелет таблицы.

 

В образовавшиеся внутри таблицы клетки записывается информация. Составленную таблицу принято называть макетом таблицы.

 

Статистическая таблица имеет свое подлежащее и сказуемое.

 

Подлежащее таблицы показывает, о каком явлении идет речь в таблице, и представляет собой группы и подгруппы, которые характеризуются рядом показателей.

 

Сказуемым таблицы называются числовые показатели, с помощью которых характеризуется объект, т. е. подлежащее таблицы.

 

Показатели, образующие подлежащее, располагают в левой части таблицы, а показатели, составляющие сказуемое, помещают справа.

 

Составленная и оформленная статистическая таблица должна иметь общий, боковые и верхние заголовки.

 

Простые таблицы не содержат в подлежащем систематизации изучаемых единиц статистической совокупности.

 

По характеру представляемого материала эти таблицы бывают собственно перечневые, территориальные и хронологические.

 

Простая таблица в подлежащем содержит перечисление единиц изучаемой совокупности.

 

Сведения простой таблицы применяют и для оценки изменения какого-либо явления во времени.

 

Групповые статистические таблицы дают более информативный материал для анализа изучаемых явлений благодаря образованным в их подлежащем группам по существенному признаку или выявлению связи между рядом показателей.

 

Комбинационными называют статистические таблицы, которые имеют в подлежащем группировку по двум или более группировочным признакам, связанным между собой.

 

Одними из ответственных моментов построения статистических таблиц являются разработка сказуемого, определение его содержания, правильное установление связи между группировочными признаками и показателями, их характеризующими.

 

Сказуемое статистических таблиц бывает простым и сложным. При простой разработке показатели сказуемого располагаются последовательно один за другим. Распределяя показатели на группы по одному или нескольким признакам в определенном сочетании, получают сложное сказуемое.

 

Статистические графики

статистический график - это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков. Представление данных таблицы ввиде графика производит более сильное впечатление, чем цифры, позволяет лучше осмыслить результаты статистического наблюдения, правильно их истолковать, значительно облегчает понимание статистического материала, делает его наглядным и доступным. Это, однако, вовсе не означает, что графики имеют лишь иллюстративное значение. Они дают новое знание о предмете исследования, являясь методом обобщения исходной информации.

 

При построении графического изображения следует соблюдать ряд требований. Прежде всего график должен быть достаточно наглядным, так как весь смысл графического изображения как метода анализа в том и состоит, чтобы наглядно изобразить статистические показатели. Кроме того, график должен быть выразительным, доходчивым и понятным.

 

График состоит из графического образа и вспомогательных элементов. Графический образ - это совокупность линий, фигур, точек, которыми изображены статистические данные. Диаметрические знаки, рисунки или образы, применяемые в статистических графиках, многообразны. Это точки, отрезки прямых линий, знаки в виде фигур различной формы, штриховки или окраски (круги, квадраты, прямоугольники и др.). Эти знаки применяются для сравнения статистических величин, изображающих абсолютные и относительные размеры сравниваемых совокупностей. Сравнение на графике производится по некоторым измерениям: площади или длине одной из сторон фигуры, местонахождению точек, их густоте, густоте штриховке, интенсивности или цвету окраски.

 

Вспомогательные элементы включают общий заголовок, условные обозначения, оси координат, шкалы с масштабами и числовую сетку.

 

 

Дециль

Дециль характеризует распределение величин совокупности, при котором девять значений дециля делят её на десять равных частей. Любая из этих десяти частей составляет 1/10 всей совокупности. Так, первый дециль отделяет 10 % наименьших величин, лежащих ниже дециля от 90 % наибольших величин, лежащих выше дециля.

 

 

Перцентиль

-ой перценти́лью называют квантиль уровня . При этом обычно рассматривают перцентили для целых , хотя данное требование не обязательно. Соответственно, медиана является 50-й перцентилью, а первый и третий квартиль — 25-й и 75-й перцентилями.

В целом, понятия квантиль и перцентиль взаимозаменяемы, также, как и шкалы исчисления вероятностей — абсолютная и процентная.

Перцентили также называются процентилями или центилями.

 

 

Типическая выборка

Типическую выборку применяют для отбора единиц из неоднородной совокупности. Она используется тогда, когда все единицы генеральной совокупности можно разбить на несколько качественно однотипных групп по признакам, которые влияют на изучаемые показатели.

При анализе предприятий такими группами могут быть: отрасль, формы собственности, специфика работы и т. д. Затем из каждой типической группы механической или собственно-случайной выборкой производят индивидуальный отбор единиц в выборочную совокупность.

Часто типическая выборка применяется при анализе сложных статистических совокупностей (например, производительность труда рабочих организации, представленных отдельными группами по квалификации). Такой вид выборки дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность.
При расчете средней ошибки типической выборки в качестве показателя вариации берут среднюю из внутригрупповых дисперсий.

 

Механическая выборка

Механическая выборка характеризуется тем, что отбор единиц в выборочную совокупность из генеральной, разбитую по нейтральному признаку на равные интервалы, в задачах статистики проводится так, что из каждой такой группы в выборку отбирается лишь одна единица.

Для того, чтобы избежать систематической ошибки, отбирается единица, которая находится в середине каждой группы.

При организации механического отбора единицы совокупности заранее располагают в определенном порядке и далее отбирают заданное число единиц механически через определенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки.

При анализе достаточно большой совокупности механический отбор по точности результатов близок к случайному. Поэтому для определения средней ошибки механической выборки пользуются формулами собственно-случайной бесповторной выборки.

 

Собственно-случайная выборка заключается в отборе единиц из генеральной совокупности наугад или наудачу без каких-либо элементов системности. Однако прежде чем производить собственно-случайный отбор, необходимо убедиться, что все без исключения единицы генеральной совокупности имеют абсолютно равные шансы попадания в выборку, в списках или перечне отсутствуют пропуски, игнорирования отдельных единиц и т.п. Следует также установить четкие границы генеральной совокупности таким образом, чтобы включение или невключение в нее отдельных единиц не вызывало сомнений. Так, например, при обследовании студентов необходимо указать, будут ли приниматься во внимание лица, находящиеся в академическом отпуске, студенты негосударственных вузов, военных училищ и т.п.; при обследовании торговых предприятий важно определиться, включит ли генеральная совокупность торговые павильоны, коммерческие палатки и прочие подобные объекты.

 

Структурные средние

 

Характеристиками структуры совокупности являются следующие структурные средние:

1. Мода (Mo) – величина признака, наиболее часто встречающаяся в совокупности, т.е. имеющая наибольшую численность в ряду распределения.

а) В дискретном ряду распределения мода определяется визуально.

б) В интервальном ряду распределения визуально можно определить только интервал, в котором заключена мода, который называется модальным интервалом. Мода будет равна:

2. Медиана (Me) – значение признака, приходящееся на середину ранжированного ряда, т.е. делящее ряд распределения на две равные части.

а) В дискретном ряду распределения определяется номер медианы по формуле:

Номер медианы показывает то значение показателя, которое и является медианой.

б) В интервальном ряду распределения медиана рассчитывается по следующей формуле:

 

Коэффициент ассоциации (coefficient of association) – оценка степени тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативного признака. Однако в тех случаях, когда один из четырех показателей отсутствует, величина коэффициента равна 1, что дает преувеличенную оценку связи между признаками.

 

 

Коэффициент корреляции (correlation coefficient) - числовая характеристика совместного распределения двух случайных величин, выражающая их взаимосвязь. Если коэффициент больше 0, то при увеличении значений одной из величин, вторая имеет тенденцию к увеличению; если меньше нуля – к снижению.

 

 

Критерий Пирсона

Критерий Пирсона вычисляется по формуле:

где fэ и fт — эмпирические и теоретические частоты.

С помощью критерия Пирсона по таблицам определяют вероятность P(х^2). Входами в таблицу являются значения х^2 и число степеней свободы k = n - р -1.

Если Р > 0,05, то считается, что эмпирические и теоретические распределения близки. При Р принадлежащим [0,02; 0,05] совпадение между ними удовлетворительное, а в других случаях — недостаточное.

 

Множественная корреляция

Множественная корреляция (multiple correlation)

М. к. - метод многомерного анализа, широко применяемый в психологии и др.поведенческих науках. М. к. можно рассматривать как расширение двумерной корреляции, а ее коэффициент - как показатель степени связи одной переменной с оптимально взвешенной комбинацией неск. др. переменных. Веса этих переменных определяются методом наименьших квадратов, так чтобы минимизировать остаточную дисперсию.

Коэффициент М. к. принимает значения от 0 до 1 и интерпретируется аналогично коэффициенту двумерной корреляции, если справедливы допущения о прямолинейности и др.характеристиках двумерных интеркорреляций, на основе к-рых вычисляется этот коэффициент.

В психологии квадрат множественной корреляции (R ²)или, как его еще наз.,коэффициент множественной детерминации, часто используется для оценки доли дисперсии зависимой переменной, приходящейся на совокупность независимых переменных. Родственный метод - множественная регрессия - используется для предсказания зависимой переменной (или критерия) по совокупности независимых переменных (или предикторов).

Индивидуальные индексы

 

Индивидуальные индексы

Показатели, характеризующие изменение более или менее однородных объектов, входящих в состав сложного явления, называются индивидуальными индексами – i_x.

p – цена q – количество t – время T – численность f – з/п F – фонд з/п S – посевная площадь y – урожайность z – себестоимость

Индекс получает название по названию индексируемой величины.

В большинстве случаев в числителе стоит текущий уровень, а в знаменателе – базисный уровень. Исключением является индекс покупательной способности рубля.

 

Индексы измеряются либо в виде процентов (%), либо в виде коэффициентов.

 

 

Статистика как наука

Статистика — это ряды цифр, которые характеризуют различные стороны жизни государства.

Статистика — это род практической деятельности людей цель которой сбор, обработка и анализ информации.

Статистика — это наука, разрабатывающая статистическую методологию т.е. набор приемов и способов сбора, обработки и анализа информации.

Таким образом, статистика — это общетеоретическая наука (комплекс научных дисциплин), которая изучает количественную сторону качественно определенных массовых социально-экономических явлений и процессов, иэ состав, распределение, размещение в пространстве, движение во времени выявляя действующие взаимозависимости и закономерности в конкретных условиях места и времени.

Объектом изучения статистики является общество, протекающие в нём процессы и закономерности развития.

Статистика как наука представляет собой целостную систему научных дисциплин:

Общая теория статистики — разрабатывает теорию статистического исследования, являющуюся методологической основой остальных отраслей статистики.

Социально-экономическая статистика (Макроэкономическая статистика). Использует методы общей теории статистики, изучает количественную сторону социально-экономических явлений и процессов на уровне национальной экономики.

Математическая статистика и теория вероятности. Изучает случайные величины, законы их распределени.

Международная статистика. Предетом международной статистики является количественная сторона явлений и процессов зарубежных стран и международных организаций.

Отраслевые статистики. Предетом изучения является количественная сторона деятельности различных отраслей экономики (Статистика промышленности, сельского хозяйства).

Общая теория статистики открывает курс изучения статистических дисциплин. Она является основополагающей дисциплиной для изучения отраслевых стастик, создаёт фундамент для усвоения и применения статистических методов анализа.

 

Предмет статистики — размеры и количественные соотношения качественно определенных социально-экономических явлений, закономерности их связи и развития в конкретных условиях места и времени.

Предмет статистики (статистика изучает):

Массовые общественные явления и их динамику при помощи статистических показателей. Требование массовости обусловлено действием закона больших чисел — при большом количестве наблюдений, действия случайных признаков взаимопогашаются. (численность населения, количество произведенной продукции)

Количественные и качественные явления (Цифровое освещение событий общества).

Количественную сторону общественных явлений в неразрывной связи с их качественным содержанием, наблюдает процесс перехода количественных изменений в качественные (закономерности).

Развитие явления во времени (динамику)