Коэффициент корреляции Пирсона и Спирмена: различия между коэффициентами. Методы расчета каждого из коэффициентов корреляции. Проверка значимости коэффициентов корреляции.

Коэффициент корреляции Пирсона:

Его также называют линейным коэффициентом корреляции. Предназначен для измерения двух переменных с интервальной и количественной шкалами при нормальном распределении.

Коэффициент корреляции Спирмена:

, где d – разница рангов

 

Коэффициент корреляции Спирмана высчитывается с помощью присвоения рангов в каждой выборке. Используется, когда по крайней мере одна переменная имеет порядковую шкалу, распределение не имеет значение.

 

Если коэффициент корреляции │R│= 0, зависимости нет

≤ 0,3, то зависимость слабая

≤ 0,7, зависимость умеренная

≤ 1, сильная зависимость

+ прямая зависимость

- обратная

 

Проверка значимости коэффициентов корреляции:

Из двумерной генеральной совокупности (X, Y) извлечена выборка объёма n и по ней найден выборочный коэффициент корреляции r_в, который оказался отличным от нуля. Поскольку выборка отобрана случайно, то нельзя заключить, что коэффициент корреляции генеральной совокупности r также отличен от нуля. Возникает необходимость при данном уровне значимости α проверить нулевую гипотезу H₀={r=0} о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе H₁={r_s≠0}.

В качестве критерия проверки нулевой гипотезы применяют случайную величину

Величина T при справедливости нулевой гипотезы имеет распределение Стьюдента с k=n-2 степенями свободы. Поэтому вычисляется эмпирическое значение критерия:

и по таблице критических точек распределения Стьюдента по выбранному уровню значимости α и числу степеней свободы k=n-2 находят критическую точку t_кр(α;k).

28. Модель классической линейной парной регрессии:

Исследователям политической науки весьма часто приходится сталкиваться с вопросами, есть ли связь между двумя переменными? Представим себе диаграмму рассеяния на которой все наблюдения выстроины соответсвенно оси oy и ox.

Предположим, что точки группируются вокруг прямой линии y=a+bx. Тогда:

Точки не стоят непосредственно на линии, но это естественно, так как на их положение влияют обе переменные. Анализ различий в положении позволяет сказать, насколько сильное влияние нучтенных факторов, действительно ли модель линейна и тп. Для описания природы связи используется термин «регрессия». Коэффициент b называется показателем наклона линии линейной регрессии.

Если мы будем наблюдать определённые распределение случайных переменных xi и yi, то мы можем увидеть, что подставив наблюдаемые значения Xi в модель, значения Y будут отличаться от y1, y2, y3 … yn. Таким образом мы будем получать y c крышечкой, то есть оценку у на основе наблюднных значений х.

Разница между yi и у с крышечкой = Еi (ошибка).

Если мы подбираем значения коэффициентов a и b так, чтобы минимизировать сумму квадратов остатков, то мы говорим, что они были получены методом наименьших квадратов (МНК).

Немного о коррелиции Пирсона и коэффициенте детерминации.

Если мы хотим узнать, насколько хорошо наша модель приближает наши данные, то мы должны узнать коэффициент детерминации.

Наша модель только частично объясняет вариацию значений y (а именно, слагаемое y с крышечкой – у среднее). Но на у влияют так же и другие факторы, которые заложен в остаток. Если бы связь была строго линейной, то Ei = 0.

R^2 – коэффициент детерминации, которые в своей сути выражает математические взаимосвязи между переменными и показывает степень их взаимосвязанных изменений.

Коэффициент Корреляции Пирсона в своей сути и является коэффициентом b в модели регрессии. Чем ближе |r| к 1, тем более четко выражена линейная связь и наоборот, если |r|=0, то линейной связи не существует, но это не исключает наличие другие связей и зависимостей.

Условия Гаусса-Маркова

Для того чтобы полученные по МНК оценки коэффициентов регрессии обладали определенными статистическими свойствами, необходимо выполнение ряда предпосылок оцениваемой модели, называемыми условиями Гаусса-Маркова.

N. B.! Рассматриваеттся модель парной регрессии, в которой наблюдения Y связаны с X следующей зависимостью: Yi = β₀ + β₁x_i + _i. На основе n выборочных наблюдений оценивается уравнение регрессии i = + + _i.

Чтобы оценки МНК были эффективны в классе линейных несмещенных оценок (BLUE), необходимо, чтобы данные обладали следующими свойствами:

1. Ошибки не носят систематического характера - (последний значок означает – при любых i). Требование, означающее несмещенность в среднем «наблюдаемых» значений зависимой переменной относительно «теоретических».

Случайный член может быть иногда положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в каком из двух возможных направлений. Если уравнение регрессии включает постоянный член (β₀), то это условие чаще всего выполняется автоматически, так как постоянный член отражает любую систематическую, но постоянную составляющую в , которой не учитывают объясняющие переменные, включённые в уравнение регрессии.

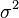2. Дисперсия ошибок одинакова и равна некоторой (гомоскедастичность). Не должно быть априорной причины для того, чтобы случайный член порождал бо́льшую ошибку в одних наблюдениях, чем в других. Так как и теоретическая дисперсия отклонений равна , то это условие можно записать так: (потому что мы знаем, что дисперсия это мат. ожидание в квадрате минус квадрат мат. ожидания). Одна из задач регрессионного анализа состоит в оценке стандартного отклонения случайного члена. Если рассматриваемое условие не выполняется, то коэффициент регрессии, найденные по методу наименьших квадратов, будут неэффективны.

3. Отсутствие автокорреляции COV ( i, j) = 0 распределены независимо от при . Это условие предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях. Если один случайный член велик и положителен в одном направлении, не должно быть систематической тенденции к тому, что он будет таким же великим и положительным (то же можно сказать и о малых, и об отрицательных остатках).

4. Все детерминированы и не все равны между собой – Если все равны между собой, то , и в уравнении оценки коэффициента наклона прямой в линейной модели в знаменателе будет ноль, из-за чего будет невозможно оценить коэффициенты β₁ и вытекающий из него β₀.

Но мы можем использовать более слабое условие – X i и i - независимы между собой: Cov(X, )=0

5. * Нормальность ошибок: N (β₀, I ) – не необходимое, но полезное условие