
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Что такое сгруппированный вариационный ряд?Содержание книги
Поиск на нашем сайте
A)Это ряд, когда реализации сгруппированы по интервалам 11. C) 12. A) 13.Что такое гистограмма, если Ni – числа реализаций по группам, B)Это статистический аналог функции распределения Как выглядит график статистической функции распределения, построенный по сгруппированным данным? A)Это непрерывная ломанная неубывающая функция, изменяющаяся от 0 до 1 15. C) 16. A) 17. B) РАЗДЕЛ 21 Какие вы знаете методы оценки параметров распределений? Укажите ошибочное утверждение. A)Метод исключения В чем заключается метод моментов при оценке параметров распределений? C)В приравнивании статистических и теоретических моментов Если распределение имеет один параметр, то при оценке его по методу моментов какие моменты надо приравнивать? A)Первые начальные моменты (теоретический и статистический) B)Надо приравнивать математическое ожидание к статистическому среднему Распределение имеет два параметра. Какие моменты надо приравнять при оценке параметров по методу моментов? Укажите ошибочное утверждение. B)Надо приравнять теоретические и статистические ассиметрию и эксцесс Можно ли применять метод моментов для оценки параметров распределения Коши, моменты которого бесконечны? C)Нельзя Можно ли применять метод наибольшего правдоподобия для оценки параметров распределения Коши, моменты которого бесконечны? A)Можно Кто разработал метод наибольшего правдоподобия? C)Фишер Какими свойствами обладает метод наибольшего правдоподобия? Укажите ошибочное утверждение. A)Он приводит к несмещенным оценкам 9. C) 10. B) 11. A) B) 12.Случайная величина X имеет плотность A) 13.Случайная величина X имеет плотность A) B) 14.Математическое ожидание C) 15.Случайная величина X имеет плотность A) B) 16. C) 17.Случайная величина X имеет плотность B) Можно ли метод наибольшего правдоподобия применять для оценки параметров, если моменты бесконечны? B)Можно Можно ли метод моментов применять для оценки параметров, если моменты бесконечны? A)Нельзя
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.61.176 (0.007 с.) |

 -середины интервалов гистограммы,
-середины интервалов гистограммы,  - частоты (статистические вероятности) попадания в соответствующие интервалы. Как определяется статистическое среднее?
- частоты (статистические вероятности) попадания в соответствующие интервалы. Как определяется статистическое среднее?
 - числа реализаций случайной величины X, попавших в соответствующие интервалы,
- числа реализаций случайной величины X, попавших в соответствующие интервалы,  ,
,  - границы интервалов. Как определяется статистическая плотность в i-ом интервале?
- границы интервалов. Как определяется статистическая плотность в i-ом интервале?

 - реализации случайной величины X. Как определяется статистический начальный момент порядка m?
- реализации случайной величины X. Как определяется статистический начальный момент порядка m?

 ; C)
; C) 
 - реализации случайной величины T, распределенной по показательному закону с плотностью
- реализации случайной величины T, распределенной по показательному закону с плотностью  . Какая формула верна для оценки параметра a?
. Какая формула верна для оценки параметра a?
 . Какие формулы верны для оценки параметров a,
. Какие формулы верны для оценки параметров a,  ?
? ,
, 
 . Математическое ожидание
. Математическое ожидание  , коэффициент вариации
, коэффициент вариации  .
.  - первый и второй начальные статистические моменты. Какие уравнения верны для оценки параметров a,
- первый и второй начальные статистические моменты. Какие уравнения верны для оценки параметров a,  ?
? ,
, 
 ,
, 
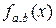 с параметрами a,b.
с параметрами a,b.  - первый и второй начальные моменты в зависимости от параметров распределения a,b; по каким уравнениям можно оценить параметры a,b?
- первый и второй начальные моменты в зависимости от параметров распределения a,b; по каким уравнениям можно оценить параметры a,b?
 дисперсия
дисперсия  . По каким уравнениям можно оценить параметры a,b?
. По каким уравнениям можно оценить параметры a,b?
 квадратичное отклонение
квадратичное отклонение  .По каким уравнениям можно оценить параметры a,b?
.По каким уравнениям можно оценить параметры a,b?

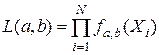
 , а - параметр,
, а - параметр,  - функция правдоподобия. Какое уравнение используется для оценки парaметра a?. Укажите ошибочное утверждение.
- функция правдоподобия. Какое уравнение используется для оценки парaметра a?. Укажите ошибочное утверждение.
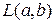 - функция правдоподобия. Как получить уравнения для оценки параметров a,b? Укажите ошибочное утверждение.
- функция правдоподобия. Как получить уравнения для оценки параметров a,b? Укажите ошибочное утверждение.



