
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Типовые законы распределения. индикатор случайного события. геометрическое распределение.равномерное распределение.Содержание книги
Поиск на нашем сайте
Дискретная СВ Х имеет геометрическое распределение, если она принимает значения 0, 1, …, ∞ с вероятностями где p – параметр распределения (0 ≤ p ≤ 1), q = 1 – p. Числовые характеристики геометрического распределения: Дискретная СВ X имеет биномиальное распределение, если она принимает значения 0, 1, …, n со следующими вероятностями: где n, p – параметры распределения (0 ≤ p ≤1), q=1 – p. Числовые характеристики биномиального распределения: Дискретная СВ Х имеет распределение Пуассона, если она принимает значения 0, 1, …, ∞ со следующими вероятностями: где a – параметр распределения (a > 0). Индикатор случайного события (случайная величина Бернулли) - это случайная величина, заданная таблицей:
Пусть ( Рассмотрим случайную величину: Геометри́ческое распределе́ние в теории вероятностей — распределение дискретнойслучайной величины равной количеству испытаний случайного эксперимента до наблюдения первого «успеха». Пусть
Построим случайную величину Функция вероятности случайной величины
Производящая функция моментов геометрического распределения имеет вид:
откуда
Непрерывное равномерное распределение— в теории вероятностей распределение, характеризующееся тем, что вероятность любого интервала зависит только от его длины. Равномерное распределение полезно при описании переменных, у которых каждое значение равновероятно, иными словами, значения переменной равномерно распределены в некоторой области. Определение Говорят, что случайная величина имеет непрерывное равномерное распределение на отрезке [a,b], где
Пишут: X ~ U (a,b) или Иногда значения плотности в граничных точках x = a и x = b меняют на другие, например 0 или Если L(ξ) = U(a,b), то Равномерное распределение U (a,b) описывает процесс «выбора точки наудачу» в интервале [a,b]. Так, если [a,b] – интервал между последовательными отправлениями автобуса от остановки, то время ожидания пассажира, не знающего расписания и пришедшего на остановку, есть случайная величина с распределением U (0,1). Распределение U (0,1) играет особую роль в методах моделирования с помощью компьютеров случайных величин с заранее заданными распределениями. Такие методы широко используют для приближенных вычислений интегралов, решений дифференциальных и интегральных уравнений и т.д. Пример (Гипотеза случайности). В некоторых случаях априори предполагается (постулируется), что исходные данные представляют собой случайную выборку из некоторого распределения, т.е. компоненты вектора данных X=(
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 853; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.008 с.) |

 q=1-p, где q и p - константы
q=1-p, где q и p - константы , P) - вероятностное пространство, А-событие, P(A) = p
, P) - вероятностное пространство, А-событие, P(A) = p
 — бесконечная последовательность независимых случайных величин сраспределением Бернулли, то есть
— бесконечная последовательность независимых случайных величин сраспределением Бернулли, то есть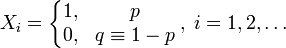
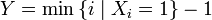 — количество «неудач» до первого «успеха». Распределение случайной величины
— количество «неудач» до первого «успеха». Распределение случайной величины  называется геометрическим с вероятностью «успеха»
называется геометрическим с вероятностью «успеха» 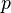 , что обозначается следующим образом:
, что обозначается следующим образом: 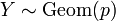 .
.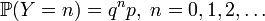
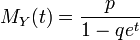 ,
, ,
, .
.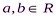 , если еёплотностьимеет вид:
, если еёплотностьимеет вид: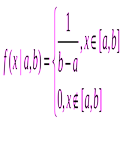

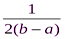 . Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.
. Так как интеграл Лебега от плотности не зависит от поведения последней на множествах меры нуль, эти вариации не влияют на вычисления связанных с этим распределением вероятностей.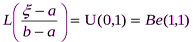
 независимы и одинаково распределены. Как правило, это предположение бывает оправдано, так как вытекает из самого характера задачи, и не подвергается сомнению. Но иногда это исходное предположение само нуждается в проверке, т.е. оно рассматривается как статистическая гипотеза
независимы и одинаково распределены. Как правило, это предположение бывает оправдано, так как вытекает из самого характера задачи, и не подвергается сомнению. Но иногда это исходное предположение само нуждается в проверке, т.е. оно рассматривается как статистическая гипотеза 
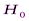 , называемая гипотезой случайности. Формализуется такая гипотеза следующим образом. Пусть
, называемая гипотезой случайности. Формализуется такая гипотеза следующим образом. Пусть  обозначает функцию распределения выборки
обозначает функцию распределения выборки 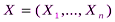 , тогда подлежащая проверки гипотеза означает утверждение
, тогда подлежащая проверки гипотеза означает утверждение 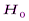 :
: 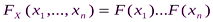 , где
, где  - некоторая одномерная функция распределения (она может быть полностью задана, либо задано семейство, которому она принадлежит, либо никак не специфицируется). Типичным примером ситуации, когда возникает необходимость проверки гипотезы случайности, является работа генератора (датчика) случайных чисел. Под случайными числами понимается последовательность
- некоторая одномерная функция распределения (она может быть полностью задана, либо задано семейство, которому она принадлежит, либо никак не специфицируется). Типичным примером ситуации, когда возникает необходимость проверки гипотезы случайности, является работа генератора (датчика) случайных чисел. Под случайными числами понимается последовательность  независимых и равномерно распределённых на отрезке [0,1] случайных величин. Такие числа широко используются в различных областях: в статистике – для моделирования случайных выборок из различных распределений, в криптографии – при получении ключей для шифрования информации, в численном анализе и т.д. В практических задачах последовательность
независимых и равномерно распределённых на отрезке [0,1] случайных величин. Такие числа широко используются в различных областях: в статистике – для моделирования случайных выборок из различных распределений, в криптографии – при получении ключей для шифрования информации, в численном анализе и т.д. В практических задачах последовательность  строят либо с использованием готовых таблиц случайных чисел, либо генерируют с помощью специальных датчиков, встроенных непосредственно в ЭВМ, либо получают программным способом по некоторому вспомогательному алгоритму (в последнем случае получаются так называемые псевдослучайные числа т.е. «очень похожие» на случайные). Во всех случаях (особенно в последнем) требуется осуществлять контроль за «качеством» вырабатываемой последовательности
строят либо с использованием готовых таблиц случайных чисел, либо генерируют с помощью специальных датчиков, встроенных непосредственно в ЭВМ, либо получают программным способом по некоторому вспомогательному алгоритму (в последнем случае получаются так называемые псевдослучайные числа т.е. «очень похожие» на случайные). Во всех случаях (особенно в последнем) требуется осуществлять контроль за «качеством» вырабатываемой последовательности 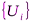 (т.е. чтобы эти числа были практически неотличимы от независимых одинаково распределенных чисел), что в математическом плане сводится к проверке гипотезы случайности.
(т.е. чтобы эти числа были практически неотличимы от независимых одинаково распределенных чисел), что в математическом плане сводится к проверке гипотезы случайности.


