
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
числовые характеристики двумерных случайных величин. условное математическое ожидание. графики регрессионных зависимостей. ⇐ ПредыдущаяСтр 3 из 3
Определение. Если на одном и том же пространстве элементарных событий Пример. Станок штампует стальные плитки. Контролируются длина Х и ширина Y. СВ Х и Y имеют свои функции распределения Определение. Функцией распределения двумерной случайной величины (Х,Y)называется функция Определение. Законом распределения дискретной двумерной случайной величины (Х,Y) называется таблица
Здесь Для двумерной дискретной СВ Свойства 1) 2) если 3)
4)
Вероятность попадания значений двумерной СВ в прямоугольник:
Определение. Двумерная случайная величина (Х,Y) называется непрерывной, если ее функция распределения Условное математическое ожидание в теории вероятностей — это среднее значение случайной величины относительно условного распределения. Будем считать, что дано вероятностное пространство
где Другое определение УМО
Такое определение конструктивно описывает алгоритм нахождения УМО: · найти математическое ожидание случайной величины · Затем в полученном выражении Пример:
Пусть
1. Регрессио́нный анализ — статистический метод исследования влияния одной или нескольких независимых переменных
2. Предсказание значения зависимой переменной с помощью независимой(-ых) 3. Определение вклада отдельных независимых переменных в вариацию зависимой 4. Строго регрессионную зависимость можно определить следующим образом. Пусть 5. 6. то функция 7. Зависимость 8. Для выяснения вопроса, насколько точно регрессионный анализ оценивает изменение 9. В матричной форме уравнение регрессии (УР) записывается в виде:
|
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 391; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.124.40 (0.006 с.) |
 заданы две случайные величины Х и Y, то говорят, что задана двумерная случайная величина (Х,Y).
заданы две случайные величины Х и Y, то говорят, что задана двумерная случайная величина (Х,Y). − двумерная СВ.
− двумерная СВ.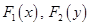 и прочие характеристики.
и прочие характеристики. .
.









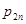


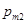

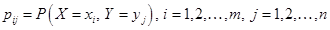 ;
;  .
. .
. :
: ;
; , то
, то 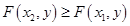 ; если
; если 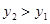 , то
, то 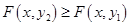 ;
; ;
; ;
; − функция распределения Х;
− функция распределения Х;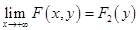 − функция распределения Y.
− функция распределения Y.
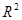 и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную смешанную частную производную 2-го порядка
и имеет всюду (за исключением, быть может, конечного числа кривых) непрерывную смешанную частную производную 2-го порядка  .
. . Пусть
. Пусть  — интегрируемая случайная величина, то есть
— интегрируемая случайная величина, то есть  . Пусть также
. Пусть также  — σ-подалгебра σ-алгебры
— σ-подалгебра σ-алгебры  . Пусть
. Пусть  другая случайная величина. Тогда условным математическим ожиданием
другая случайная величина. Тогда условным математическим ожиданием 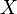 относительно
относительно  называется
называется ,
,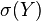 — σ-алгебра, порождённая случайной величиной
— σ-алгебра, порождённая случайной величиной 
 ;
;

 — произвольное событие, и
— произвольное событие, и  — его индикатор. Тогда условной вероятностью
— его индикатор. Тогда условной вероятностью  относительно
относительно 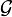 называется
называется .
. на зависимую переменную
на зависимую переменную  — случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений
— случайные величины с заданным совместным распределением вероятностей. Если для каждого набора значений 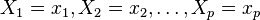 определено условное математическое ожидание
определено условное математическое ожидание (уравнение регрессии в общем виде),
(уравнение регрессии в общем виде),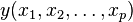 называется регрессией величины
называется регрессией величины  , а её график — линией регрессии
, а её график — линией регрессии 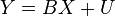 , где
, где  — матрица ошибок. При обратимой матрице X◤X получается вектор-столбец коэффициентов B с учётом U◤U=min(B). В частном случае для Х=(±1) матрица X◤X является рототабельной, и УР может быть использовано при анализе временны́х рядов и обработке технических данных.
— матрица ошибок. При обратимой матрице X◤X получается вектор-столбец коэффициентов B с учётом U◤U=min(B). В частном случае для Х=(±1) матрица X◤X является рототабельной, и УР может быть использовано при анализе временны́х рядов и обработке технических данных.


