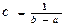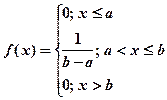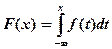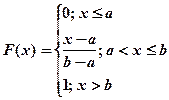Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое ожидание дискретной случайной величины и ее свойства.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Математическое ожидание дискретной случайной величины Х называется взвешенная сумма всех ее значений:
Свойства: 1. М(С) = С, С =const 2. M(C+X)=M(X)=C 3. M(C·X)=C·M(X) 4. M(X+Y)=M(X)+M(Y) 5. Если X, Y – независимые, то M(X·Y)=M(X) ·M(Y) Дисперсия дискретной случайной величины и ее свойства. Дисперсия случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания D(X) = M[(X-mX)2] или D(X) = M(X2) – (M(X))2; Свойства: 1.D(C) = 0; C=const 2.D(X+C)=D(X) 3.D(C·X)=C2·D(X) 4.Если X, Y – независимые, то D(X+Y)=D(X) ·(D(Y) Средним квадратичным отклонением Х называется неотрицательное значение квадратного корня из дисперсии: Биноминальный закон распределения: ряд распределения и основные числовые характеристики.
M(X)=np; D(X)=np(1-p) Геометрический закон распределения.
Пуассоновский закон распределения: ряд распределения и основные числовые характеристики. Если n→∞, а р→0, то M(X)=D(X)= λ Непрерывная случайная величина. Функция распределения и функция плотности вероятности, их свойства. Случайная величина Х называется непрерывной, если она примет более чем счетное число значений. fx(x) называется плотностью распределения случайной величины Х. График плотности распределении случайной величины Х называется кривой распределения случайной величины.
Свойства плотности распределения: * для всех * ∫f(z)dz = 1; * для всех точек Вероятность того, что непрерывная случайная величина Х примет конкретное число значения, равна нулю для всех Вероятность попадания непрерывной случайной величины в числовой промежуток можно рассчитать: для всех Р(с≤X≤d) = P(c≤X≤d) = P(c≤X≤d) = P(c<X<d) = F(d)-F(c) = ∫f(x)dx. 18. Математическое ожидание и дисперсия непрерывной случайной величины и их свойства (без доказательства). Математическое ожидание непрерывной с.в. называется число Свойства: 1.М(С) = С, С =const 2.М(С·Х) = С·М(Х), С = const 3.Если X,Y – дискретные с.в., то М(Х+Y) = М(Х) + М(Y) Дисперсия случайной величины:
Свойства: 1.D(C) = 0 2.D(C·X) = C2·D(X) 3.Если X,Y – дискретные с.в., то D(X+Y) = D(X) + D(Y) Начальные и центральные моменты. Начальным моментом порядка k случайной величины Х называют математическое ожидание величины Xk: vk=[M(X)]k. Оценка начального момента: В частности, начальный момент первого порядка равен математическому ожиданию: v1 = M(x). Центральным моментом порядка k случайной величины Х называют математическое ожидание величины [Х-М(Х)]k: μk = М[Х-М(Х)]=0; Оценка центрального момента: В частности, центральный момент первого порядка равен 0: μ1 = М(Х-М(Х))=0; Центральный момент второго порядка равен дисперсии: μ2 = М(Х – М(Х))2 = D(X).
Плотность распределения:
Плотность распределения:
Функция распределения:
Показательный закон распределения: плотность и функция распределения, основные числовые характеристики. Функция распределения:
Плотность распределения:
Поток событий. Простейший поток. Распределение промежутка времени между последовательными событиями простейшего потока. Поток событий – среднее число событий, происходящих в единицу времени. Стационный поток – его плотность: постоянная величина. Поток без последействия – если вероятность попадания определенного числа событий на определенный промежуток времени не зависимо от того, когда и в какие моменты событие появлялось до этого. Ординарный поток – если вероятность попадания на элементарный промежуток времени двух или более событий пренебрежительно мала с вероятностью попадания на этот же промежуток одного события. Все эти потоки – простейшие. 23. Нормальный закон распределения: функция плотности и функция распределения, основные числовые характеристики. (Закон Гаусса). X ~ N(m,σ)
M(X)=m; D(X)=σ²
|
||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.67.90 (0.01 с.) |

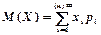
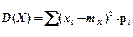
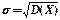
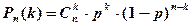 , где n – число испытаний в схеме Бернулли, р – вероятность появления события в каждом испытании. Х = {0,1,2,…,n}
, где n – число испытаний в схеме Бернулли, р – вероятность появления события в каждом испытании. Х = {0,1,2,…,n} , где р – вероятность появления события в каждом испытании; X = {1,2,3,…,k,…}
, где р – вероятность появления события в каждом испытании; X = {1,2,3,…,k,…}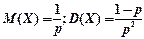
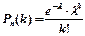 , где X = {0,1,2,…,k,…}; λ>0; λ=np – среднее число появлений события в n испытаний.
, где X = {0,1,2,…,k,…}; λ>0; λ=np – среднее число появлений события в n испытаний.

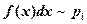
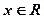 : f(x)≥0;
: f(x)≥0;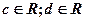 : таких, что с<d:
: таких, что с<d:


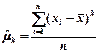
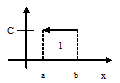 20. Равномерный закон распределения: плотность и функция распределения, основные числовые характеристики.
20. Равномерный закон распределения: плотность и функция распределения, основные числовые характеристики.