Алгебра случайных событий, диаграммы Вьенна-Эйлера.

Сумма событий А и В называется такое событие, которое происходит, когда происходит либо А, либо В, либо оба события.

Произведением А и В называется событие, которое происходит, если в опыте происходят оба события.

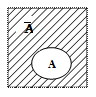
Событием Ā, противоположное событию А называется событие, которое происходит всякий раз, когда не наступает событие А.

A\B (дополнение А до В) – происходит А, но не происходит В

Классическое определение вероятности. Комбинаторика.

– классическое определение вероятности.

m – общее число исходов

n – число исходов, благоприятствующих наступлению события А..

Комбинаторика – раздел математики, изучающий расположение объектов в соответствии со специальными правилами и подсчитывает количество способов таких расположений. Комбинаторика возникла в 18 веке. Рассматривается как раздел теории множеств.

Аксиоматическое построение теории вероятностей.

Аксиома 1. «аксиома неотрицательности» P(A)≥0

Аксиома 2. «аксиома нормированности» P(Ω)=1

Аксиома 3. «аксиома аддитивности» Если события А и В несовместны (АВ=Ø), то P(A+B)=P(A)+P(B)

Теорема о вероятности суммы событий.

Для любых событий Р(А+В) = Р(А) + Р(В) – Р(АВ) (док-во в лекции)

Условная вероятность. Зависимые и независимые события. Теоремы о вероятности произведения событий.

Р(А|В) – вероятность события А, если событие В уже произошло – условная вероятность.

Событие А называют независимым, от события В, если вероятность события А не меняется в зависимости от того, происходит или нет событие В.

Теорема умножения вероятностей: Р(АВ) = Р(А|В)·Р(В) = Р(В|А)·Р(А)

Теорема умножения вероятностей независимых событий: Р(АВ) = Р(А)·Р(В)

По определению условной вероятности,

Формула полной вероятности.

Есть события Н₁, Н₂,….,Н_n попарно несовместные и образуют полную группу. Такие события называют гипотезами. Пусть есть некоторое событие А. А=АН₁+АН₂+…+АН_n (слагаемые этой суммы попарно несовместны).

Формула Байеса.

Н₁, Н₂,….,Н_n A

Схема Бернулли. Формула Бернулли. Наивероятнейшее число успехов.

Пусть проводится конечное число n последовательных испытаний, в каждом из которых некоторое событие А может либо наступить «успех», либо не наступить «неудача», причем эти испытания удовлетворяют следующим условиям:

· Каждое испытание случайно относительно события А.т.е. до проведения испытания нельзя сказать, появится А или нет;

· Испытания проводятся в одинаковых с вероятностной точки зрения условиях, т.е. вероятность успеха в каждом отдельно взятом испытании равна р и не меняется от испытания к испытанию;

· Испытания независимы, т.е. исход любого из них никак не влияет ни исходы других испытаний.

Такая последовательность испытаний называется схемой Бернулли или биноминальной схемой, а сами испытания – испытаниями Бернулли.

Для расчета вероятности Р_n(к) того, что в серии из n испытаний Бернулли окажется ровно k успешных, применяется формула Бернулли: (k = 0,1,2,…n).

10. Понятие случайной величины. Дискретная случайная величина, способы ее задания: ряд распределения.

Случайной величиной называется величина, которая в каждом испытании (при каждом наблюдении) принимает одно из множества своих возможных значений, заранее не известно, какое.

Дискретная с.в. – с.в., множество возможных значений которой конечно или счетно.

Ряд распределения с.в. (ряд распределения вероятности). График ряда распределения задается многоугольником распределения – ломанная, которая соединяет точки с координатами (x_i,p_i)

X	x1	x2	x3	…	xk	…
P	p1	p2	p3	…	pk	…

Закон распределения с.в.: p_k=P({X=x_k})

Функция распределения дискретной случайной величины и ее свойства.

Функцией распределения случайной величины Х называется функция F_X(x) = P(X< x), .

Под (X< x) понимается событие, состоящее в том, что случайная величина Х примет значение, меньшее, чем число х. Если известно, о какой случайной величине идет речь, то индекс, обозначающий эту случайную величину, опускается: F_X(x) = F(x).

Свойства:

1.

2.

3.

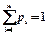
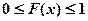
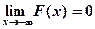
4.Если , то