Интервальные оценки математического ожидания нормального распределения

Интервальная оценка математического ожидания при известной дисперсии. Построим доверительный интервал для математического ожидания наблюдаемой случайной величины при известной дисперсии по выборке .

Образуем вспомогательную случайную величину , где - точечная оценка математического ожидания . Согласно утверждению 1 теоремы Фишера, случайная величина имеет нормальное распределение и ее функция распределения не зависит от неизвестного параметра.

Доверительный интервал, соответствующий надежности β, определяется из условия (3.20), которое в нашем случае имеет вид

. (3.31)

Неравенства и являются равносильными, то есть для любой выборки они выполняются или не выполняются одновременно, поэтому соотношение (3.31) можно записать в виде

. (3.32)

Поскольку случайная величина имеет стандартное нормальное распределение, вероятность в левой части формулы (3.32) можно выразить через нормальную стандартную функцию распределения по формуле (3.7):

. (3.33)

Приравняв правую часть формулы (3.33) заданной доверительной вероятности β, получим уравнение . Решение этого уравнения является квантилью порядка стандартного нормального распределения и определяется по таблице значений стандартной нормальной функции распределения (см. табл. В Приложения). Предельная ошибка вычисляется по формуле . Таким образом, доверительным интервалом математического ожидания, соответствующим надежности β, является интервал

. (3.34)

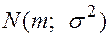Интервальная оценка математического ожидания при неизвестной дисперсии. По выборке из нормального распределения требуется построить доверительный интервал для неизвестного математического ожидания при неизвестной дисперсии D=σ².

Введем новую случайную величину , где - несмещенная выборочная дисперсия.

Статистика согласно утверждению 3 теоремы Фишера имеет распределение Стьюдента с степенями свободы. Рассуждая аналогично случаю, когда дисперсия известна, получим следующий доверительный интервал для математического ожидания:

, (3.35)

где - квантиль порядка распределения Стьюдента. В отличие от доверительного интервала (3.34) длина интервала (3.35) случайна и зависит от случайной величины . Поскольку с увеличением числа степеней свободы распределение Стьюдента быстро приближается к нормальному, то для больших выборок интервалы (3.34) и (3.35) практически совпадают.

Пример 3.2. По результатам 9 измерений напряжения батареи получено среднее арифметическое значение 30,6В. Точность вольтметра характеризуется средним квадратическим отклонением 0,2В. Требуется найти доверительный интервал для истинного значения напряжения батареи, соответствующий доверительной вероятности β=0,95, предполагая, что контролируемый признак имеет нормальный закон распределения.

Решение. Для нахождения доверительного интервала воспользуемся формулой (3.34). Квантиль порядка 0,975 найдем по таблице А Приложения: . Поскольку предельная ошибка , то доверительный интервал имеет вид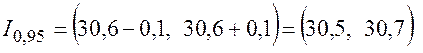

.